Show:
Solving Systems of Equations
by Graphing
Solving Systems of Equations
by Substitution
Solving Systems of Equations
by Elimination
Systems of Linear Inequalities
Miscellaneous
100
Solve the system of linear equations by graphing. y = 2x + 5 y = 1/2x - 1
Solution: (-4, -3)
100
Solve the system of equations by substitution. y = 2x + 3 y = 5x
5x = 2x + 3 y = 5(1) Solution: (1, 5) 3x = 3 y = 5 x = 1
100
Solve the system of equations by elimination. x + 3y = -2 x - 3y = 16
2x = 14 7 + 3y = -2 Solution: (7, -3) x = 7 3y = -9 y = -3
100
Tell whether the ordered pair is a solution of the system of linear inequalities. y < 5 (-1, 5) y > x - 4
5 is not less than 5 No
100

Write the equation of a line that is Parallel to the line y = 3x +5 and through the point (1, -7)

y=3x-10

200
Solve the system of equations by graphing. y = -x - 4 y = 3/5x + 4
Solution: (-5, 1)
200
Solve the system of equations by substitution. y = x - 4 y = 4x - 10
x - 4 = 4x - 10 y = 2 - 4 Solution: (2, -2) 10 - 4 = 4x - x y = -2 6 = 3x 2 = x
200
Solve the system of equations by elimination. -5x + 2y = 13 5x + y = -1
3y = 12 5x + 4 = -1 Solution: (-1, 4) y = 4 5x = -5 x = -1
200

Find the feasible region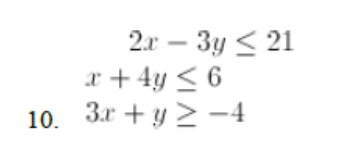

see teacher

200
Find the slope of the line through the given points. (1, -2), (7, -2)
0
300

You are part of the rescue team in a ship at sea.  One of your divers is 250 feet below sea level, and she injured herself.  She only has a 7 minute supply of air in her tank, and can only rise towards the surface at a rate of 10 feet per minute.  You are sending down a rescue sub.  The sub can descend at a rate of 30 feet per minute.  *Note: Normally, the diver would take safety stops when ascending to avoid suffering from the bends, but in this emergency, the diver will be placed in a decompression chamber when they get her to the surface, if they get her in time.

see teacher

300
Solve the system of equations by substitution. y - x = 0 2x - 5y = 9
y = x 2x - 5x = 9 y = x Solution: (-3, -3) -3x = 9 y = -3 x = -3
300

Solve the system of equations by elimination. -6x + 5y = 25 -2x - 4y = 14

 Solution: (-5, -1) 

300

Graph the system of linear inequalities. Describe the solution. 

2x + y < -1 

2x + y > 3

No solution

300

The Fine Threads Company produces sleeveless and regular t-shirts. It takes 1 hour to produce each sleeveless t-shirt and 1.5 hours to produce each regular t-shirt. The company has a total of 975 hours of production time available. Due to demand, the total number of shirts produced in a week should not exceed 800. Would it be feasible for Fine Threads to produce 400 sleeveless and 400 regular t-shirts each week? Justify your answer.

see teacher for feasible region

400
Solve the system of equations by graphing. x - y = 7 0.5x + y = 5
Solution: (8, 1)
400
Solve the system of equations by substitution. 4x - 2y = 14 y = 1/2x - 1
4x - 2(1/2x - 1) = 14 y = 1/2(4) - 1 4x - x + 2 = 14 y = 2 - 1 3x + 2 = 14 y = 1 3x = 12 x = 4 Solution: (4, 1)
400

Solve the system by elimination:

1/3x+1/4y=10

8x+6y=2

no solution

400

Find the solution region 

3x+4y>8, y > -1, x > -3

see graph paper

400

Elijah has made a commitment to exercise in order to lose weight and improve overall fitness.  Elijah would like to burn at least 3000 calories per week through exercise but wants to schedule at most 7 hours of exercise each week.  Elijah will do both running and weight lifting for exercise.  Running burns 600 calories per hour, and weight lifting burns 400 calories per hour.  What combinations would be the best for Elijah?

see graph

500
Write a system of equations for the following situation. Then solve by graphing. A kicker on a football team scores 1 point for making an extra point and 3 points for making a field goal. The kicker makes a total of 8 extra points and field goals in a game and scores 12 points. Write and solve a system of linear equations to find the number x of extra points and the number of field goals. Explain what the solution means.
System: x + y = 8 Solution: (6, 2) x + 3y = 12 The kicker made 6 extra points and 2 2 field goals.
500
Write a system of equations for the situation. Solve the system by substitution. There are a total of 64 students in a drama club and a yearbook club. The drama club has 10 more students than the yearbook club. How many students are in the drama club? the yearbook club?
x + y = 64 y + 10 + y = 64 x = 27 + 10 2y + 10 = 64 x = 37 x = y + 10 2y = 54 y = 27 drama: 37 students yearbook: 27 students
500
Write a system of equations for the situation. Solve by elimination. A landscaper buys 4 peonies and 9 geraniums for $190. Another landscaper buys 5 peonies and 6 geraniums for $185. Write and solve a system of linear equations to find the cost of each peony.
4x + 9y = 190 Solution: x = 25; $25 per peony 5x + 6y = 185
500

Write a system of linear inequalities for this situation. Graph the inequalities. You can spend at most $21 on fruit. Blueberries cost $4 per pound and strawberries cost $3 per pound. You need at least 3 pounds to make muffins. Is it possible to buy 4 pound of blueberries and 1 pound of strawberries in this situation?

x = pounds of blueberries x + y > 3 (or equal to) y = pounds of strawberries 4x + 3y < 21 ( or equal to) Yes this is more than 3 pounds and costs $19, which is less than $21.

500
You can spend at most $60 on lace. Cotton lace is $2 per yard and linen lace is $3 per yard. Write an inequality for the amounts of lace you can buy. Can you buy 12 yards of cotton lace and 15 yards of linen lace? Explain
2x + 3y < 60 (or equal to) No you cannot buy 12 yards of cotton lace and 15 yards of linen lace because (12, 15) is not a solution of the inequality.