Reflections
Rotations
Translations
Name that transformation
Misc.
100
Reflect (2, 3) over the x-axis
(2, -3)
100
Rotate (2, 3) 90 degrees clockwise
(3, -2)
100
(2,3) moves 2 units right
(4, 3)
100
A ( -5, 6) ---> A' (-5, -6)
B (4, 6) ---> B' (4, -6)
C (3, 2) ---> C' (3, -2)
A reflection over the X axis
100
what quadrant will the answer be in?
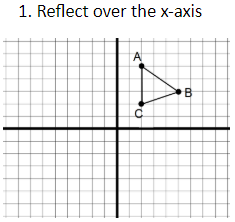
quadrant 4 (bottom right)
200
Reflect (-3, 2) along the line x = -4
(-5,2)
200
Rotate (-3, 2) 270 clockwise
(-2, -3)
200
(2, 3) moves 4 units up
(2, 7)
200
A (1, 2) ---> A' (-2, 1)
B (-3, 4) ---> B' (-4, -3)
C (0,2) ---> C' (-2, 0)
90 degree rotation counter clockwise
200
PROVIDE EACH TEAM WHITEBOARD GRAPH PAPER
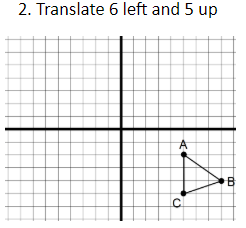
List the coordinate points on your white board !!!
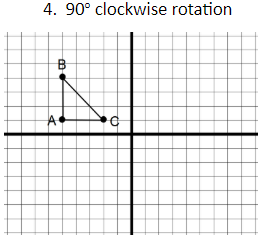
A (-1,3)
B (2,1)
C (-1,0)
300
Reflect (6, -4) over the y-axis
(-6, -4)
300
Rotate (6, -4) 180 degrees
(-6, 4)
300
(2, 3) moves along vector <-3,-1>
(-1, 2)
300
A (3, -1) ---> A' (-1, -8)
B (2, -2) ---> B' (-2, -9)
C (-3, -4) ---> C' (-7, -11)
translation 4 left and 7 down
300
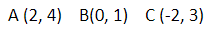
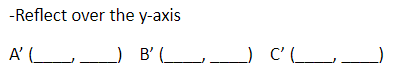
A'(-2, 4)
B'(0,1)
C'(2, 3)
400
Reflect (0, 9) along the line y = -4
(0,-17)
400
(0, 9) transforms to (-9, 0)... identify the rotation
90 degrees counter clockwise
400
(2, 3) moves along notation (x+5, y+5)
(7, 8)
400
A (-8, 2) ---> A' (-2, -8)
B (4, -12) ---> A' (12, 4)
C (12, -4) ---> A' (4, 12)
rotation 90 degrees counter clockwise
400
what quadrant will the new image be in?
quadrant 1 (top right)
500
Reflect (-4, -4) over the line x = 4 THEN reflect over the line y = 3
(-12,10)
500
(-4, -4) turns into (4, 4)... name the rotation
180 degrees
500
(-7, -1) moves 3 units left, 1 unit down
(-10, -2)
500
what combination of transformations was used to get from ABC to A'B'C'
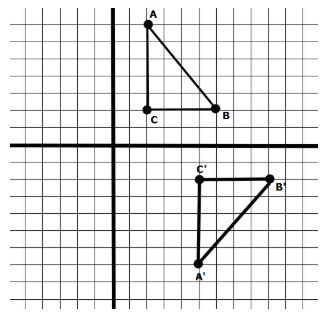
There are two or them
3 to the right, reflect over x axis
500
what quadrant will the new image be in?
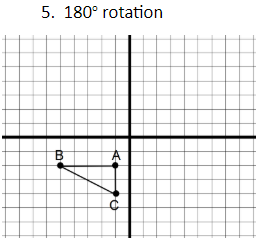
quadrant 1 (top right)