900 + 2 + 50 = _______
What is 952?
What do the numbers in this equation represent?
8 x 9 = 72
What is 8 groups, 9 IEG, and total items/product?
Solve 52 - 37 = ____.
What is 15?
Write 5,882 in expanded form.
What is 5,000 + 800 + 80 + 2 ?
Third Grade is recycling cans. They collected 143 cans on Monday and 156 cans on Tuesday. On Wednesday they collected 57 more cans. How many cans did they collect in all?
What is 356 cans?
Complete the pattern below:
450, 460, 470, ____, _______, _______, _______
BONUS 100 POINTS: If the pattern continues, will it eventually land on 700? How do you know?
What is 480, 490, 500, 510?
BONUS: What is Yes? What is all the numbers in the pattern have a 0 in ones place so it will land on 700?
Kymani will ride his bike a total of 56 miles over 7 days. He will ride the same number of miles each day. What is the total number of miles Kymani will ride each day?
a. 8
b. 9
c. 49
d. 63
What is 8?

What is 27 pencils?
___ = 633 -149
What is 484?
Our class had 345 paper clips. We used 89 on Tuesday and 114 on Wednesday. How many paper clips do we have left?
What is 142 paper clips?
<img data-fr-image-pasted="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAzsAAALICAYAAABYXu4sAAAgAElEQVR4AezdCbg9yVnX8RN2QjAQkuhkn5BlJpkwQxICGpOgqEHBBTfUKK4P7oq44wI8xl3B/RF3RdwQF1yiUYhRkggzYZgkM0lIMJOQhbAESAIGEMbn0+H3T01Pn3PPuffc+7/n3F89T9/uU13LW996q+qtruq+D7rvvvvuW9WVQAmUQAmUQAmUQAmUQAmUwJER+LAjK0+LUwIlUAIlUAIlUAIlUAIlUAITgU52qgglUAIlUAIlUAIlUAIlUAJHSaCTnaOs1haqBEqgBEqgBEqgBEqgBEqgk53qQAmUQAmUQAmUQAmUQAmUwFES6GTnKKu1hSqBEiiBEiiBEiiBEiiBEuhkpzpQAiVQAiVQAiVQAiVQAiVwlAQ62TnKam2hSqAESqAESqAESqAESqAEOtmpDpRACZRACZRACZRACZRACRwlgU52jrJaW6gSKIESKIESKIESKIESKIFOdqoDJVACJVACJVACJVACJVACR0mgk52jrNYWqgRKoARKoARKoARKoARKoJOd6kAJlEAJlEAJlEAJlEAJlMBREuhk5yirtYUqgRIogRIogRIogRIogRLoZKc6UAIlUAIlUAIlUAIlUAIlcJQEOtk5ymptoUqgBEqgBEqgBEqgBEqgBDrZqQ6UQAmUQAmUQAmUQAmUQAkcJYFOdo6yWluoEiiBEiiBEiiBEiiBEiiBTnaqAyVQAiVQAiVQAiVQAiVQAkdJoJOdo6zWFqoESqAESqAESqAESqAESqCTnepACZRACZRACZRACZRACZTAURLoZOcoq7WFKoESKIESKIESKIESKIES6GSnOlACJVACJVACJVACJVACJXCUBDrZOcpqbaFKoARKoARKoARKoARKoAQ62akOlEAJlEAJlEAJlEAJlEAJHCWBTnaOslpbqBIogRIogRIogRIogRIogU52qgMlUAIlUAIlUAIlUAIlUAJHSaCTnaOs1haqBEqgBEqgBEqgBEqgBEqgk53qQAmUQAmUQAmUQAmUQAmUwFES6GTnKKu1hSqBEiiBEiiBEiiBEiiBEuhkpzpQAiVQAiVQAiVQAiVQAiVwlAQ62TnKam2hSqAESqAESqAESqAESqAEOtmpDpRACZRACZRACZRACZRACRwlgU52jrJaW6gSKIESKIESKIESKIESKIFOdqoDJVACJVACJVACJVACJVACR0mgk52jrNYWqgRKoARKoARKoARKoARKoJOd6kAJlEAJlEAJlEAJlEAJlMBREuhk5yirtYUqgRIogRIogRIogRIogRLoZKc6UAIlUAIlUAIlUAIlUAIlcJQEOtk5ymptoUqgBEqgBEqgBEqgBEqgBDrZqQ6UQAmUQAmUQAmUQAmUQAkcJYFOdo6yWluoEiiBEiiBEiiBEiiBEiiBTna21IH/8B/+w8pRt5o4nIXFO9/5ztWXfdmXnSvK5OFct5p4v/rVry6KCyTwd/7O31mV+f6B6zt25XqR/TfZ1P0hOrLP++Z77733AX6XqWwXWbcpt/r9H//jf+TnVueL1gv1eJ7j30Vw/0f/6B/V7tpKuy5HoH3ZXecxdh7cZEeH8cf+2B9bPf/5z189+9nPXv3CX/gLV1/5lV+5+qEf+qFzre3/+B//48pRt5o4nIXFu971rtWXf/mXnyvK5OFct5p4azt1F0fgPDrsi5P+8uak79hVly+y/75oo3asKTq36fg3/+bfjMEfcE32ed9ssjP3e0DE6+hxkXWbYmJ82Sc76uw8x7+L4G6ycxZbI/XV88UQ2JfddR5j50FNdgAwwfnhH/7h1Ytf/OLVV33VV60+8zM/c/VX/spfWT3taU879wnPxahLcymBEjgtgd/6W3/r1EecNn7jlcAhE6D/nribtCwdr3/9668Vz3j6iEc8Yq9P/43Hxui6EiiBErhMBD7iMgmzSZa3vvWtKx3513/910+rOQn7rGc9a/UFX/AFq//6X//r6uM+7uPi3XMJlMAVJHDTTTddwVKff5EZzti2jz1/1mfN4ff//t8/PQQ8KZ3HPe5xK+Pnx3/8x58UdOv70nv/+9+/dfhdAtLBpzzlKXuVd5f8G7YEQoA9+oEPfGD11Kc+NV5HcT7Wcqmcg5nsmMzo6GxbmztPp37tr/21c+/+LoESuGIEft/v+31XrMQXU1xP6++4447JOL6YHJvLeRP47M/+7JVjn+4v/+W/vM/k7pcWHXzZy1621UTufhH7owT2TODP/Jk/s3rjG9+481bGPYux9+SOtVxAHdQ2tn0+gdq7ljTBEiiBEiiBEiiBEiiBEiiBS0XgYFZ2LI9bxjab3nbp8Hu+53tW/+2//bfV7bffPr3nYxvG53/+568e9ahHPaASvLj5v/7X/5rCPe95z1t93ud93totG//lv/yXaducd4fI9aIXvWgxrCVBK1Lk5qT7i3/xL95qGd7eavL7EIP45Pve7/3e1Qte8IIpDdtJ3P8n/+SfrL7927999fCHP3xa3br55psfUDYewpJFGSPLC1/4wmnP9mKE1WqlnPjZlmDLwy/9pb90tS79pDFyJOvP/bk/d2MeiZezD03823/7b6/JSUbHuu0zyiX8yFjd7eqU9X//7/89vdCJpTyx38bZ+/6FX/iF0953L1OSRRrKbg/76CKv8HPnSybij/dGPfBCrPqgB+RTH5w0yfC2t73tRD0QXh294hWvuFavVkUf//jHz8W59vt//s//ufrGb/zGiQ09WBc+HJTfewNeVvRe3TonXW6Js/gPfehD73dv1I2HPOQhq+c+97nXGCSPpTSV9zM+4zOm9LQBB6c9bloRxvWf/tN/unrDG96wkp/69CRcHj/4gz+4uMocOeZn5aFf6g7DX/7Lf/nafowe4J22qo+h01awRzfyePCDHzyVJzoxhnNNZuWWvxVy+W+qc3Giq0kLx7SzUUfdp6fu08EbbrhhYkPuuYuOJG3pjWzn4U/6vasuL6VnTPnP//k/T/Ws3dKVn/2zf/bWfc5JfVTy1MfgQ+/Sjyp//DeNT0ljn2d15linM6fJa6ndqiNl5vRfL3/5y1f0FbdtVpboTJz0jXfcXAe1B+3GcdLYLP7I/qQ2mfyXzmPboj94Lun+Ulx+2sI2dspZOcorNknk5Pe+971v9e///b+f+pvo/9IOmnXy8x/b/zbteQwfWXZhJk/1Z0yM/UPH5vrk/nve854H6Hg4LPWrOGufaaNjudW18YD87373u699dXFs08JHF9Pn63PZAtuW0RggLl1STnpvPBU/9qY8vuZrvma6jznbcmksncuif9a/jWF3LdfYxj73cz930abG2PgZu2TXdoEj3dQ2jF36jE/7tE9b/Zpf82vGKrnf9TjOYjXKdjArOwR3fPqnf/pUufcr4cIPhX7iE5+4+pIv+ZLVh33Yh00D8N/+23979ehHP/oBS48+0fjrf/2vn8J97Md+7OoP/aE/tHrmM5+5kOpq9Rt+w29Y/abf9JumsBTMsp+wKmV0lvOf8IQnrP7W3/pbU97CSvexj33sVi+EMnS++Iu/eOVrJBoJI0Uav+N3/I7Vr/pVv2qa9CmfcJT3LW95y/SRBuHnTmMR9k/9qT81hRXeNb+lL8ooizx/xa/4Favv+77vm+LcfffdU/pf9EVfNE9++s1gUN7f9bt+1zU22N96662TrIuRZp7f9m3ftnryk598TU51IT2TpjlfUf/dv/t3UxmwVqaUSxrk2cZJ1/YIZfXVobCU57qyztP1Ltk/+2f/bOLjnDR+1s/6WQ/4ZKuGL/yS02nP70UP6Ogv+SW/5Joe0Fe6qJzqUf0kXx/roP9zl7Ji+uM//uNTeB2Jept/bjZxdSyf8zmfc42N8LfccsuklwmTM9mlQ3ew1MFvcjpqx5JTp/N79F4bUk56icG841tKUxtlMIn/R//oH53ip52vG9S1I1wZAcmPjggvj22364T5r/t1v26qO2lhyLCd1zUO0tVHpa2mjyGLAXB0Iw/G3RIP+asPdagPkf9Xf/VXT3W4pCNj+owE+uzgDDjj74TVTuhcdFA71qaWGCmzdvszf+bPnNIa2a7TweQznsN1F10e4+fa+y3qIvWMkbrSp895izPvc+gR7uv6qOSD9c//+T9/9cpXvvKaEcUPJ0YNDuvGp6Sx77O+RdvYp1tqt/LwUE6d/4W/8BemstJX7UkfdpIbde4bvuEbFnVQGtrD7/7dv/va+LNubBZWv4F9dDZtcklnN8mX/jFtyzgsXX01HT3J0QFtexs75awcyfPzft7Pm/rQpz/96ZNo/Bjq6VfJ/4t+0S96QL+6qRzz9q9vVrf6nR/4gR94QFSMx/4izHZhr93iHPsHf3nedttt92u3+iLtc+7+4T/8h1P/q95Hh8cv+2W/bNKh0T/XHpzTxze/+c3TZCe66XecfkP/Mfb55CQvubdxbAFy0I+Mp/oIfSQ9x1Ue8k8fqo+f96HsA/bQKAsm+quR9zblklbKpf1GniV7Q1h2QtpX6njJPl3HI7qZMVue7N+lMVtYfMdyRs8wnNx9B+Tuvffe+571rGfdt1qt7nvhC19431d91Vfd9453vGOxBMJ+xVd8xQPufeEXfuEUNzfEl97LX/7yeN2XfJzjxHvwgx983+d+7ufe9/73vz/e9733ve+976abbnpAXi95yUvuc4xOPPJ/yZd8yei9eK1s8nvKU54yyZNAb3jDGyb/xz3ucVP54+/84he/+L6HPOQh9333d3/3NW/hH/7whz9APgHwmZed/+d93ufd97znPe9+6fC/4447JnnIhUeccmEwZ+O+cO6NTjryHR3WZB/TdV/aZHnRi140Bp/YSmOpjnEgo/vyOskJPzITXt2JP+rAunSEw/jrv/7r7xfka77mayY5xrSXyp5IL3vZyx7AJXqAAV2Li3zr9GDOnIyY4Djqr/SkhT0Oo/Nb+nMGZJLe2GbEC4d5+DHN8Vpdz+s791/wghfc7x6WGI9pk1s/MJZnKU1tbkm3pIXJvBxf/dVfPYX/uq/7uogzndWjehCHfCc5+Yb5WHfi0QNs58yVSVnnTpsc+w3h1vEY8xJv3odIO3o16uY8z/G3ul1qS+THds7Q7yW20hFe/qNTHuG3kUca4TrWvfSks6TLS3qh71AH83LhJ7z6G9OXtrznfQ6ZtavoprKJGxcW8zLL+4u/+IsTbMqLXs3DXQuwxQX59MMp7/wcGSU1lzN+0hjdUr803h+v5+3WvbSDebnCc647Y3rjNbnIMnfKSB+cR6cel8bm9GvGxtHpv5d0dgyTa2WiZ/qDkan799xzz9TmtL3RLfEWd65P4iiLvm10u3LEK7pNj8k6H0ewuOGGG+5XBv3PvF8d5ch1uOtfkk/upa8k89iGMibO6zxtZD6GLulT2i3Oo5Mn3R/zjH03l08Yx7yO6KR+9SSn7EtjgLJK1/2xH5YeebX5pfqe55c2R39H/XJNRzGXx+jI7t7Yh5JHHc9lWVfOTeUiy7xc0v/SL/3Sa30WzvQOw3kdZ6wY5RvlH68xVBZpjy727zxt9TjXbfHED5P792pjqpf4WkENLgoBrOttACqSShcnLko1NsjcG88qWQXOlUYYlTjvmMa447XGrCJPcjrGsbMaw6vYpTQwEGc00jTIeYMe01KuMS08cB0b2Bhe5+G+eHFknRvXueesgY8ypUGMYeZyjPdSrnFwIvMowxjeNZ1Yx28edt1vecwH6KWw8vmiL/qipVtblT0Ro4v57Rw9mHfs7unwxrpLvCVeZNxURxmE0g7ouXqedyrJA/u5zstDW9jWSWNdHc4HOZ3WJvmT51KaGBnQU7aEddY2xkmEMNr50oRD+Aw2SwPdmK5r+W6SOYPTklzztNTDWNcntTnxtTN1uO6B0Lzs8zzH30ttidzSnxsoibfUL0qHQbLk5v3EUhh+u+qyOHO9iOzqYMm5r+7G9o//On0d0xAndZXBdkwnYZVjHbuE2fUsTRMo+S0d4zg5ypl8+EljdEv90nh/vJ63W/ewYIgsOX3Y2P6WwsSPXGSZO3WizS61o7kOpt7X9Wvz8PO88luZTHZGnrnnHKNsNLKXeI9xxuu5neLerhzxkj9ZtK2lCQx20dUx/22uxd3Uv+grxwcb2Pu9ztjHXj89urk+ZVxa127dn7db5ZZ2HLnoS2yZUW/o4jZtXJilMUAdy39MM/k6p88n5yaXNufB29zpt3FcymPbPlSa5Bz1k99pyxUZpUfvluyh2CWjLZh48/MmXZ+PW/Kkh+vaYsIfzDs741KXvYYOexFtP7DMZcnPvsO5s7xlSdBWriVnidB+Xct6lpLt1156p0dcy71LH0mwl94y6pKzpGmJ0z5PzvLeto5ctu7Nnfzm+/eFiV9ksWfS/uiv+7qvmydx7betcrZx2Dcsvu0+yrluPz8283di7HG1V3YdY2WwjLtpb7g0/sgf+SNr0yCj91m8r6Vc8ppvc7pWqJ/cz73p/hg219KUdvjRnW2d/edLDtOkt3R/Gz96sLR/2DLy0vtr0QN7fMf78z3uY962Y/ze3/t7p3pSl//8n//z6f0f70ot1as6tR937uZ7puf3T/v7V//qX736i3/xL046pBze11lqi+vSt/S99N7XvH7oKTffHpd0tQt1bYvXNm4Tc6zsQ5bnnJv2aF94+g16OToy+PKcNvUbf+NvnPqt1HvCZY8/PXDMHZ1Keef3tvltW5v99vqEJR3BammblLpccvO6WAoTv01c57qcOOM5e8Dn3BOGrmDrfRp5bdPnJG7OtuzZZvKSl7zkfvvjc18/Slb9nryW2njC7nKm68a1y+TW9Y/6sLP2j8ppzNqmfUdn1/Vr63R2iSW9mLe5hNPvkon+LI3hCZfzSXZKwu3KkU30J//kn5z0bOn9STpozKd/yrOOY/Kfn8VfZy9hSRfThrD3/i8e6/oL/ZR+b11bMC7pM9e1W2PC2G7Jq0zy9s/oOeOWMOTOPb85feaf/tN/ero+zR/xpbWki9JLn29r1boxZsx3qb7pHIZLeWzqQzHH1nYwLucxv3XXJ5VrHm+d3MJt296X0hB/XsaMc14RcMxdxrmDnOykMCqbwqh4xrDKHDsW+yO/4iu+YnrXZfRP/Jxf+tKXTvs3TZg47xr8pb/0lx6wN3Bdx5Z0xrPOi2wMdB163l+w1/IjPmI77LvkN+ad6yiVTmedizFMSeRncha/dXE+9VM/9dpLosLIxz92daxzm4yTpPEH/sAfWBd98s/kI+XaJCcZt3XeW1JXOlp64j0JzguI27qz1tWmfPaV9klM6Ek6C3rg2j7Yy+DU9X/6T/9paqfefeCy73hT247s2uA2Tpk3tRdpqI9tJzu7MJc2HffewT/+x//4fv3G/H+XkDE87LHn5jy0E4O8Y53bht26uNI/jY6sM47W5bPkvyvXeRpkP6me3Q+7bfqcMQ/tx4OtT/7kT16tk1Udq+s/9+f+3OqP//E/PtW3ftK4tctEfsz3sl7vqw9bV75t0z+tzi7ly1De5OhP+tNN4ba1U6SxbTmTn/fA9B1e1F5yjG8f+PnDf/gPT++UCeNF9z/xJ/7E/Wyppbj81ul2wrN72EBc2pB+apPbZIRrV7u0W/n4GIv2xfb6hE/4hOmdybw746Mz3t8xQXHfwyV+p3Xb9isewG/jdq3vpTRNZr2T5aM6I/ttxzBpblOuMe99yL1tGmTbZpw7mA8UjCDn1wyhTHZyz1PPf/2v//X0T0gZEAzaHAmTs/jueanaaoCX9xgQSytFiXPS2ctilMv/ptBAk/emCcFJae563xMQzlPidY5snCe0HENkU3hh5g1VPiaVdpisO5aeKk0Z/uQfafiHsevi88/Ld5E1so/p5HouY/znZxNkdfU7f+fvXL33ve+d6it15WXHi3SZzJ1XnicxUe9hy9jSpjbVh3vn5ebGvXw8rWZA3nPPPdPDiJ/4iZ+YnpifpK+7yGgV7aT0Tro/5rcLc/Ho4qte9appRXbsN5baT3gYoN0Pj7QLbcqXezbVof7ptE7610tHduU6LyPZT6pH99MehOfCdp7e/Ld+1GT0O77jO6Y6tQth7rQxL+x+13d917T64ym4l2p/+2//7fOg/b0nAvvUWS96b3Kj/qwLt4udsi6NTf5/9+/+3Wmi46X2dfaMjymkX33xi1+8evvb3751v3pSO/QAcd6G9O2b+qRND2C0mV3aLTbsO/26Ly6K62V8XyPjTIR8WUz7/Ff/6l9NE7yzPGjYtl/ZxwOfTfWee1ax6JgPg+Ae28YZl23dNuXaNq19hyPbNuPcUUx2wPM0QKHjzGZ9dcgAMrpN28g8MfCE37KY5VlPPE7jLBXaHmL7wrzhntQ5nCa/dXEs33mykqeTS+EsC+sI8rTEEyCyLw3O4jPI8RmdJ1ynZZV0pKHOtnFkJTPZ17mlLVZLYYVT15a4553cedRVdHSJb56ALcm5D79NTEz6PIXM00p6wIimy+flsFjiYEAizzpHrz2ZM3gbSDfp97o01vkrv77E9qMlZzvTLvltYo7tyDz9hgnI+FlQcsy3sY2yGbSsCIRH2oWykPW8JtHSpyOb6mqUc5/Xm7jOdXkpX1sksN+k39ilPdC5k/qceT7qMJNJq5FLui6OHQqesJuwOs7al87l6O8PEYjObqr3D4XefGW8Wlen2pxxNPqzLqXT2Cnr0lryp1u2TNmiTwfXTXjEpePGQTq7bb/KFljXv2Aj7zDI+Sz6bQvsLu02TLQv/aK8tf1sAWNLkEtb1+ev2zqVdE46i79pfEifv26l7aT0d71Pv0xgjQ8pc9LYNKYkTM4nlSvhrsc59beuLUamg5nsmImaiCy5DG6ZrQvjc9NWVubOcu3oPJ1Z+gTsj/3Yj639/OAYf+la3tw8f53C0h72pTT25ffn//yfn7aXLU3y+Nk69nt+z++5lh3GD3vYw6Z9vtc8hwvbLrIcHW+rIjr2pc8KKnOeQCf80lkajP1rnwkcApFTGpaZ48hM9nXl+nt/7+8l6MbzOj3R8S2957AxsS1uGlBsk/M0aXTKse1kb4y3y7U6WuKrjmzhNJBk6ZgBrUO2/L3kPA08q7y+mT/nIC/beubOJ3+zsjfeO0s7HdPJtQHBOxQ+cblkxPvU8aZtFkkn53XM3fcEf2SefsOnW+fur/21v3Y/L/3hOh4f/uEfPoW1NeMjP/Ijp61S94v8kz88CJLOaR1DgY785t/8mxcNHhPSs+rIOtnWcV3S5aU06Dn261ZRtP8777xzeh8q8Tf1Oesmx9qRFR5bYvPJWOmRU1879mn8f/RHf/QB446+Qfi6sxOIzq7r13bRWeOD9wiXnE/gGkcZ2ZvcuvFnbqdsSmObeyYxf/AP/sFplXFs89rn0m6TbftVtgCbYMl5V0hf6Z1CDnufgfZZ/SV9xn6pTxvTtiKyqd0qy7zdiq+fYl9op1ZzRpetbN5vPssWNmkqq/zX9Qfp8y9qZWedfpFvbseNTObXm8pFn5bssHka5/U749y6tphxbruXR85Lyh3S9ZTdzFwj0WjnHyjwrfdRgX7Lb/kt0/9oyXsYnhZr2Hmynqy/8zu/c3phzX1pMHY8NWSEWfo7jTPAmW3aCvelX/qlk1xm0SY6P+Nn/IwHbAM7TR7bxmGUKpf/ceCcztdLgzqG7BEf07P0zfg1QOefsEZ+/OdPP3D3RFKDuOuuu6aVEhw1AkaaTu4xj3nMmMUDrikkVgwCT6FGOXHzzx/tt437bb/tt03G6FK5En4bQ4vBQZcs9eYfTGJDB+arcsn7rGdGE6MZS7rCqP7Kr/zKqS62kfm0+VvqxVed55/bJm9P8v7sn/2z90v6b/yNvzGx0ZmoW/UcPdC5+bjFWRwZfFwEd+1Vx+zJG0N2zt5DiS//8i+fHiAIjx3dYsxLZ5/OoCt9OqjsZLF96V/+y385TQZxtNVjGxfmZLaCyMjGXD17EuW9jbj0G9qXPfMmxngr58d8zMdM2xASVn848pCW9oyHyUfcv/gX/2IycGzRVO/yV3e2nerzbrzxxgTdeMaAjmon5JcWR0f87w7/U0q71daxsg/eE06r2+fhwnVbXV6Sgb6rY++lSUcZMaGDnlirm3FMWepz6IkHK+J4f0GdzZ0VY++F6mf8nzjXnH/s63fq2lN3BuL48Eld+d8WdGK+oj7P59h/qx/GsK1+npCnv9613OnXPEDDms6mndnitK3OMrrp+Wte85prbUs62qGPEml7J7lt7ZST0tnmPnbsIW3VeE3n0xeRG0/672HTtv0qvbTtVhsa27++Uvu3u2ZsQ3/9r//1qT8a+wt56g+F34ZZ2q32pE3qN6VhzPbBqnm7xcaHpzgTmq/92q+9Hy6THw9OPYT0AG4bRxfJrE0aO9k7/JSVfvrYj7zS52vH3p8y+furf/WvbpPFXsLQrzzMZ2MZJ9i26scW5LnbtVyY6/+0o7N82GEux66/6Y2VS/od5nRbXXzgAx+YxrkP/7KTptK75npO4VWCylIAxrinCYxajVSjnRcjxrIGZJKk89GYvaimIevgGM8aCoMGJCsTBi0GwT/4B//gfgOXVRpxPuVTPuUBJaRAJlEaX9yv/JW/ckqTUmkQGiNlILcyKMsmt5Rmwm+SRTmscJE1DguN/Zu+6ZumBuoJh8ZpeZPRPXfiMm4tF1Nm8uPMD3tuzkL9qAdGqX+kKg9PKXVGjKSP+qiPupaNp0Ya/ZyBwUddqDMdiTQ48edySs+EbF4udacjx0AeOuNxknRNiJ+80Dnh45/VqX8dAT+dtDJ6D2Kpzsd0MF+Xj3rHZqyPz/qsz5qie7oSA4ZuGDw91R+5bNIDYf1DryX5yMQI1RFzfqs/+dA/5YteMmAxnnPyW516AmRQF56RoTPxbls+uhEWmzgkzHhWh+r7m7/5m6cByiRHWdSfp6K2DaVsdEOd2jb1N//m35wMRnWvnY5yL7UNdcAQ1dbnbim8MPLDi+H+2te+dopmtQc/+kBr8ikAACAASURBVIn9Sf8QUb7KJw5u3iG0L5y/CYkJB30dnX7DxMT+8oQ1qdRvjf0GnRp5kCk8PvETP/FakvROn0NebVf/5t1EE0Ts5vlfizi7oN/ao3pn4Ovr9CHYS1//R0fITE4GugGIfo5urpfjvaW2Mt7P9Wl0eameya6O6Zr3BZXNP/ikcwbJsT+X91KfY+KiLrB80pOeNIm41GblRRc8XNOXauPGIx+rkYa8yahPHlebPvqjP3rSP32UfE5ym/jO4y7JyU85xz7oR37kR6a+fPSbp5XfS33SpnpdCp+05mc6+C3f8i1TX6Fd0n86uFS3ibtURnWhX+OMb3RW+8w/up3rbNIaz8r0c37Oz5neHdQ/qr+k4wGhPmzePy7Jsq2dIu9dOS71x+rQ5Pt1r3vdpOd0kF75p4/6VfpvIsKAxWmTw11b0a9o/2wdHLR/k3htYv4BA/qszY39hTzJoL+Yh1/Sj7TbBz3oQdOXZtl30tD//f2///dXz3nOcx4gNj1Rbm06zBNIemwSxvL4An/uL53JKz0TKzaDhxx50OEeztq5f6abPtc/PdXnn8RVfpvaHO7+8bQH53M31xH1Qy5jK1nVjQfPrvX96mG0TXYtlzTY4XnAFttunT1EJ7XbMc95Gfyel2MMs9TepadNa8dhLo0v+IIvmNoiOR/k+9ZjQr0ugRIogRJYT8Bg6SMmDOK6EiiBEiiBEiiBy03gYN7ZudwYK10JlMCxELBysc65Z/tRXrZdF67+JVACJVACJVACl4NAJzuXox4qRQmUwCUgYKvJLbfcsnbVxjsVtgF4F66uBEqgBEqgBErg8hPoNrbLX0eVsARK4AIJ2Mfva00PfehDp/cq7Pe1ouPlV/uAfcDipD3HFyhusyqBEiiBEiiBEthAoJOdDXB6qwRK4GoS8ElgHwnwUr6Xob1U+gt+wS+YPiLhxdS6EiiBEiiBEiiBwyDQyc5h1FOlLIESKIESKIESKIESKIES2JFA39nZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUQAmUQAmUQAmUwI4EOtnZEViDl0AJlEAJlEAJlEAJlEAJHAaBTnYOo54qZQmUQAmUwDkR+L//9/9eS/n//b//t/qJn/iJ1Y//+I9PR26Mv12PTnjHfffdN3n/2I/92Mrh9zzsGK/XJVACJVAC50/gQfeldz7/vJpDCZRACZRACVxKAobCDIcf9mEffA6Y386j34Me9KD7TWQ+4iM+YiqTCc8YjqfJDr/4X8rCV6gSKIESOGICnewcceW2aCVQAiVQAtsRGCcqVmVMTj78wz/8WmT3f+RHfmRlovMxH/Mx1/zHizEN/vPfY9hel0AJlEAJXAyBTnYuhnNzKYESKIESuKQEbF0bV1+sxmSi8/73v3/1Qz/0Q9fuP/jBD1593/d93+qjPuqjJr+EtfpjcmNL3EMe8pDVwx72sGliZHIk/az+XFIEFasESqAEjpbAB9fej7Z4LVgJlEAJlEAJbCaQic6P/uiPXpvUvO9971vde++9q3e/+92r97znPauP/diPnbaumbiYCIljcuO3lR7nd7zjHau3vOUtq5tvvnn1WZ/1WatHPepRq4/8yI/cnHnvlkAJlEAJnCuBTnbOFW8TL4ESKIESuOwE8m6OCYwVGKs5d9555zRx+cRP/MTVp33ap60e+chHTqs27gvHWdXx2+rN2972ttX3fu/3rr7ne75nWtWx5c19k52u6lx2Dah8JVACx0ygk51jrt2WrQQumECMRsafp955ZyHG4UniiJ+48zhJ66Q0ev/6E1BX6tExutQvv2z/cj36j+FzPW4D8z5NVlZy/6xn6SWPD3zgA6u3vvWtq3e+852rxz3ucasbb7xx9fjHP366b+uaycsP//APr2xni3vXu961evvb376yMvTEJz5xmhhhkFWd6m5I9VwCJVACF0+gk52LZ94cS+AoCYwTHQU0WZkbuwxcRiXj0uG3eAkbo9fZwUgUjpundZQQj6RQ40QndZk6TB2n/k0Q+GWFJAj4JQ6dcdCTcWUlYc96pmdx3/3d37369m//9unT0Y997GNXVnZSHvnTWRMdE57Idfvtt69MeD7hEz5hmvCYFFVfQ7TnEiiBEri+BDrZub78m3sJHA0BxiljkGM8xkB0nd/uMwS5GLjOMWzdd50Jjt8xRGs8TtgO4k/qal53JgruqVfbvt7whjdMEwbvw5g4JF70w9lkyH1bxKy2/PSf/tNXt91229ovop0GkHzpnFWdu+++e3XHHXesnvSkJ61e/epXT6sz0dFM0PxWNis33ufJKpCVIB8zcF95nLmxXKeRr3FKoARKoAROT6CTndOza8wSKIGBAAM2jiGY9xQYuJ6Ce4eB8cc/xiDj0RHDkPHoHgPXF60+/uM//prByL9GYwhf/rP64ka9UH+2oXmv5XWve91074YbbpjqORMhYcRN/I/+6I+eJhNe/n/FK14xbRG75ZZb9gqA/tFLExX5P/OZz5wOeks/I5OyuHb+KT/lp0wyvPSlL1190id90rTlTRp0X1m4xNursE2sBEqgBEpgJwKd7OyEq4FLoATWEWDkMQIZqTFw+eWl7fe+973TJCYTHPccVnpG45DB6fO9nqwzapPuunzrfzkJZLIyl852Lys6VlGs0JjsmCSoc5ODcYIgDas6vnBm0vNxH/dx0+TDJMRkeF8uemuSLZ+f+lN/6soWtkyC3Kej5KG/Ju4cWR/+8IdPHzQQJrrtrEz86G/KtS95m04JlEAJlMD2BDrZ2Z5VQ5ZACWxJgFHImLW9x/sPfnvPgeEaw48hGMPWtcMT/9e+9rWr7/zO75zimOyIy+W8pQgNdokIqDsThO/6ru+atoj52tmznvWsaaJgpcd9ujB3/Gwlow9PfepTV9///d8/rahkVWUe/rS/6d4oQybYPinN32HyEkePOfKZrCeMyZFJkckOP9fCSL+uBEqgBErg+hD4UO99ffJvriVQAkdGgMHH2HvjG984/Z8SW9Fuuumm6eVtT83dZwAKwxj0RP+hD33oNDn6hm/4hum+l8IZiO4xLIWrwbisKDGunbHd5uX4GPMxyBnyrtVLnDDcablLK+k5W415+ctfvrrrrrum1RN1a1ta9CX50AsTIPWeifJznvOcafsaPVFO901E9uXIp/yZ0LiOPGM55vlZCcLJ9svoqHPii6s8ypi052n0dwmUQAmUwPkS6GTnfPk29RK4MgRiHDL8fNHqnnvumd7FMNF5xCMece0zvIy/OEYhA5bBaHLkP9M/4QlPmFZ4sgokrHB1ywRGniaTWJlYZPVhKRaDPAZ+6k08fnHjdfzOera69+QnP3l6x8V7LiYB6t5EwEoguUzW+LlWHveUxVlZyRuZzyrPWeOP8pAJQ7K7di8MO9E5K+nGL4ESKIHTE+hk5/TsGrMESmAg4Cm3iQ4Dz9esXvOa16ye8YxnTFuPvK8TY5ARy/ntmsFre5MtbwxEkx9puWY4cjEapx/9s0gAo0wKR0N7KbB64kau6iNunPiM17l/2vPDHvawaTua/1tjImNrGxnISya/M0n7gR/4gan+/c8bYck3yntaGfYZj9wcRuPBLxO2kes+825aJVACJVAC2xHoZGc7Tg1VAiVwAgFPr01ebDF605veNH2dyhY27+Aw+BiDXAxExiAj1le2HJ76+6ywJ/ve3THhycTohKyv9O2sJGCcyaGJQ3jP4QijDtST8zhJimGeuLm3r0mGdNWzd27Ioa7lqZ6dyRP9kGfCKIMwDmmknPOyXdRvMoRNVqf81gawJ58j3Midcl2UjM2nBEqgBErggwQ62akmlEAJ7IUAY9WTeduRfMnKC+i2KvHPNp4YiAzBGIDey7jzzjunuAxhkxxxHEsrEHsR9ogSYXibuGCFmZf4rYZYGVly+Fo9UQd4C6/efAzC/4k5T6OcfNKnBw6/OX70gR+5yOjMJUyu6dJ5yjhlesIfspEhkx6Tdr+tYJqom+QrQ5xy1ZVACZRACVwfAp3sXB/uzbUEjpJADFiGn/8mv/R54ExyGOfCOTNgY9zmf50AFCPRvUyYjhLcGQqFkQMjL/3fe++9q7e//e3XeM6TFs6hHhjn3q3yeXCfdX70ox891YkJhjBJe57GaX9L0yTAakhkTl50Ic7kQbh5nYvDmWRcTxc5yO7A8n3ve9/0D0a9r2bFiozKW1cCJVACJXB9CXSyc335N/cSOBoCDLt8qpehygjMVinXXJ6E5zcjMdcxgk2QPB2X3mgsJu7RANtTQXBxYGZFx/tP/k/Mox71qLU5ZBXCqpqJx7vf/e5p4hPeYe18VjemZZIgb2f17h4d8Nv1GJY+5J0e/nFkJPO+nXTHfCLPUj5kz2qa+z6sYeIYPxPHbNFzPzq+lFb9SmBbAqN+ps2I63rJ0enq3hKZ+l01Ap3sXLUab3lL4JwIZMDNE3kDM8N2HGyFSThi5LdzjGDxxMlZOE/4x4H+nIpwkMkyaExyrOaYHNx4442rm2+++QGrImPhrAAJ/573vGfauubrbQz01E3Yn5exlLpMfnMdIat76t1KX7bo2SJpQmH73b6dvMhBf00YfR1wlGvMjzxksV3NSpp/eupz6U984hMnmb2TRP6UT3lzPabT6xLYhQAdGnUpv9Oe5mnN9Vc4x9x/Hq+/S+DYCHSyc2w12vKUwAERMFjHCMyTdb9d121H4Ad/8AdX3/Zt3zZ95IGR/chHPnJaqdm0+mEVyKqOCaYVICsTqYftcj1dqBhbzlZ0RsPLb45M/OmAw29nEzKTOfdMNEw49uWkr/xkkI/JjknPujwinwmOj2uYgPnSnHfV/APUTs73VTNNZ04g7TQ66Pe6yQu9Fi5hnBN/nm5/l8AxE+hk55hrt2UrgUtOwMBrMGZkGphjdGZQdq9uMwHbp77jO75jemcEx//zf/7PtNKTycM8tlUdkx33fRr84Q9/+GQsMdjP2zHKbO/KJEJ9x5nUxAnnt7P3d4QzqfMxBROdTRO5pLHLeZ2erTMMsYsRqSw+xOF9J5Mfq2wmSmRMuuvS2UXGhr3aBOiTSXQc3cokZ2xHue8szNiuxnu9LoGrROBDLecqlbplLYESuBQEDMaZ4BjIHQxFW5cY4blvUK/BuFxlXoy3ovMpn/Ip0z9vFYoxngnFPJZVCx8k8P+MGOjYmujEcJqH3+dvdc1oS52rX248k4P8MeAYa7aKmeR4t4j/vrexyYMMzriYtDztaU9bq3PCYeardrYCvutd75o+xkFu/pmsK4t0q7v71KKrmRado1/vf//7r61w0is6tk6/hM/DhXwxEL114a8m2Zb6KhDoZOcq1HLLWAKXlECMXAM549wkx7YgW4G8ZM+/A/PmymNcP+Yxj1nddttt02TnJGZWHkw4sDaxxDeTj805nf1unkybuLiOASd/usA4458JAkPOBIesT3jCE1af/MmfPJXRVjPG2z6dvB14mPDYDrjJRUbv7Vh1yuSSzMqVckijOryJZO9tQ4BuWrX1f8voF73jtOF1Tjj9g5XHpz/96dfirAtf/xI4VgKd7BxrzbZcJXAABGIExuD2v2He9ra3TU/LDeKbnloeQPEuRESrHA7Gt0mEa++2+DLekrMSZHKRCYZwDHXG1Hk7n2V2ML7Iq35NvDiGmWuy0AcTmm/5lm+ZPhTgfzbdeuut0/9jUkYfU9i3k3/0DZuTnDDiYE0mRqUyjUfCnJRW75fASQQ8AHr961+/uuuuu6Z3w7SBtHF6u+Topq2f9DTt29nvuhK4SgQ62blKtd2ylsA5EmCgMvQ4Wyds8TEI88ukZp49fwOvp/RWdN75zndORvgNN9wwbQti/HpC3gF6Tu5DvzNZwDmrHTGCPhTqQ1fuMcwZ4iYWzjHKU38fCn32q9S9PExgbfuyUkM31H10JHKob3GUy4qJLWVPecpTpqfSwgjPiKNj+3Qpu3OuN6UfAxJzMjlndSfxnd07NqcelA0D5xjS9Eq7N/nzXpjtkqkr4dSrI3WNmXrm574PPKhXK2tX1WGDh3fr8hBD33j33XdPKzuYm/j7B8DRufCfM1MP4vkAiXQ58ffpUq/SjBzy0NbHNko30j7W5U8XIp90Hfm9Ls4u/pFBumTV13BhHj0ke8qVMPN8Eod/2rh4m/reeRon/Saj8pNFfiOLtBv+uEZe59EpU9xY/tE/94/53MnOMdduy1YCF0hAR2pg0CHbevSt3/qt02BnIFjXsQpvJcc/tvTkklF70003TYMzo6lu/wQMoIwQ59SZAXI+SO47ZzrgH836+ptjNIRiOGRAJ5sJkVUoKzze36Ir0linS/uWd1N6MSyi22Tix9hhhDB43DtvpptkPM97qQflU2fh4GyCY/WBge1/ZmGhLjnhc/gtHTpo9eGOO+5YvfCFL1w985nPnBiuMzLPs1yXIW0MuRi2+sdXvvKVU1sw+cFT3/iIRzxiCpO2syQ7I9gKkPd80m5SX0vhT+OX+iR3ZOaXPsY1/0x0/F5y2nzakfvSS9qRfSneLn50KvlHv/xO+tqvB250mB+Zc2+eD3k5ZVPWn/bTftreV5ylnfpyLc/Ut4cI5NPfkHssW8pIvsjvfupAOtITLvo2L9+x/e5k59hqtOUpgetEQOepY3UwXnwhzLVO1r0lx99gbmuTPej+P4yBnJHLCHLEcFyKX7/dCeSJoIHOoX7GgXL3FJdjSDsDrRCu1a33i5785Cff7948BQO6FSArfCbO0vKU2qDu2v3L4JSJ4TAaIVgyIHKQMwbLZZB5XzKk7NKLwcSo9k6JFTn/c8g7VrmnreMwspAGQ1483NSv8K6vqqPfHF50/vbbb5/agHfy3PMxDP76xjB1XnJLbQXzfbrUr3qVdtK3MpUHVmR1P/Iu5Z92I1yctMIjfmc5R7bIqt1y/JXDOPS1X/u1E1sPZKyc0ckllzYvLcfzn//86aMmS2FP6ydvEynpyw8jDDHxoRnbvsnIH2NlSBnlKZxDXPe0yWwBFm4Me1oZDyXe1e1RDqWGKmcJHAiBdKjOth496UlPmp4k6ZzXDcYZKA2MOm1P/k10pJH0FF+nrNO+Sp3zeVV7Bkvpe9Ln90VwHevQtQGciw64Th1HHmH4JZxBPQP+5Hmd/0Q2HMlFZ+ky+RkqKUfCXWdx95Z96kmC6k+5tVv/qNZE5/GPf/zqqU996mRYubekY+qWIe9hhzBWKjA0Gb/Kjs5ggBmmjFqTRqubtgZmQhidwmydwzhHwkQn8/ss51EPpKMeySMPEx2rstqDVQj3tJPIPc/XhNdXJRn3tjEKR3Zp7VNm+abPkW6u6e43f/M3T9up7S7wnqAxjDxLTv0ol38obKugeomuL4U/jV9kow9hp7285CUvmXZCGDN9yAcrrCNreOGXOhLW4UGTOnLPBInfVXDrW8lVKH3LWAIlsDcCOv8MUHnPwoDHb50TR0duULfVxWDhyZPO2KGD54TR8acTX5de/U8mkHrC02DNOLV6cuONN54ceccQqfvUW878HfktWb9HYyl+MXjymy4Idz1dZHfGk65iyRhlNNnSQk73OWGO1alDBrl/UuuDEto+w/zNb37zxCRtPAZWWIjDSPSVPat9r3vd664ZdOo8ht6xcttULozoDh1yeCLPj3HKMVDdH9vGUnoYijf2nftkS4axDctL+lmR+sZv/MbpvSPvF+nXtdt19ZrJAv153vOeN8WT3j4dlvQwcpNFviYsJt500lbqbBE0/ozlG2VRFvd9bMXug0w0xjBnvU6bIQOu5HzZy142vbslz8/+7M+evrIXvYisOYvjsKX0Va961TV9Sh1clYmOeuhk56za2PglUAITAR2oQSQDiY50287UQGHwSOcsjVxL3L19D3xXtdoM+AZHfO1Nt0fdJ239n57zdBmAk4ffGXSjM2OYXAuTQzjX52FYRK5tzpGbjGTyVNX2IttgTNrJl5fLt0nv0MKk3MruMFk2WWHkMtA8fcZI+8cm9Zd27PyGN7xhmhTaLvSwhz1sYqaNmzSG76Fx2Ye82icOVkQ4ukSnPDiK8c1Ax109pJ0s5S2Mdp56EmZT+KU0NvmlnpKPure1Sp/yile8YrrWr3zmZ37mVMfyJs+SkxadsP05MjuLk3yW4p3GT7oZT7RZspo8PPvZz54mBjjjrTybHF11qA9y7pOtfMOBPN5p9TCBXlh50oebQDrkrzyRIXKIr60Jq206hMMzOrVvtpt4Xc97m2vyekrWvEugBA6KQAZfnadrHSxjZ1NnKpzB3IChI04nrUN2L3F19kn/oKBckLB4ZbA7KUuDukHcRMfh3RicbSEM/5PS2OZ+Bl71xmXgZswZgEdDInWb/N0XnlxJx2/ObwM+Y2SfjgzycJCRTpJjyWEtHP2mm1ZznG3DsYXLOUbrUvzz8gujbdNP+xIv9RTeqYultHIPB+WkU1YfrNA897nPndJSv0nTOXlp77YsZcItXPJntPmoAe7SvoouPEyWccICOwdmHL/U0yZGqae0OWHjtyneLvfIon7JrV36PLYJi3pmlHPucaMeTB7DH+lo02O59q0DSQ/LtBU6pw80IeNvopZw5F3Hyz1tXj9h213qaSjSmS9T51Zm/vt//+9TelZC5Wk3RMpAjrjIO7KWjjLhS07OJCnxE/eYz53sHHPttmwlcAAEdMTjkcFOZ+3g3K9bT4ARFOMxrDKozWPlibEtG4xUg2eMqHnYff8mm0HXOfXrOgN08osOODOayOzpP6OJcZJ/qJjw+ziTy4EFNm984xsnPktp7cG7pAAAIABJREFUMxLIQjZbsRh3+Yen733ve689gV+Ke55+qftd85jHU77RWNo2PVuQHOGT9ut36pxhpl5NCK0C1G1HIHWEKX5pPyYyo7E7puYeR1fDX7+QyccY9rTX0iWPOjZRsMonj2zl1Kbc5yL7afM6r3jkSzkiZ86R/bzyPildzHA14fFAwUMpjOt2I9DJzm68GroESuCcCGTwlrwBxpGB3LX7GfDPSYSDTJbxb/uHVRpP6zDaZMww5IW3jcEXhLyrw0C/KLbycTCIYgSnflMBqX+/8+Ktp6+2R3mKSnaD/r4cOTj6Jj/v3pBhExNGnJUd7zx5Sdh/qDdx9GRbetKisxfpUo5t8wx3cipPXPzze9tzjGppYZfyx+CNfNKv240AdnmAgXPqa+Q8T1G4sBbO9Sadnsc/6bf6dUjXQwK6rx969KMfPfVBtnamzqUVWU5K96Lvj1xSJnJHfy9anuSX/DG1kqPP29S3J17PDyTQyc4DmdSnBErggggYZOaDit8GToO5J5b7HJwvqFgXmk2MGCwNhAxwKw4xjObCmCzYImOS43+aWDUxkOYp8Dz8Pn8bvGP8kHusW/I75s4KAKPp3nvvnf4fk3cA1j3Jnsfd9nf0ULpervfPLeWD5TqXyRrW9tN7CRv/keNSedaltw//XfNL+LEN8suxq0wxznJO/OST86gHCdPzZgJ0K5NG25hMyuknPfzABz6wGNk9D0PGife8bhYjbumpPtOenclETpMdD1XIOd+atmXSFxpMP4TtPtnsqwC46mOybXddv76v/I41nU52jrVmW64SOAACBheHwYah6ZrhzbhllBukDUIZ5A+gSBcuooHQioLPpD7ykY+cOI5GyFwgX8nKtjUrJNgzmsaJxzzOvn4nDwO269H4jcz86YHfrq2ceLJpG5vPphr0Y2DtS67IQd+kjYeDHEtO+OgllladPHW1hYvMDD7HWJaldPbtl3Lskq44ZE1Zw36XNDaFHWXKtXOuN8XtvQ8RoJcmNXTtHe94x6R/tnNu4mjrky1PdFQdc/R2n07+dEabdk3nOWe/5Re/feZ73mmR3XE9nfxxxTdHJj3XU65DzLuTnUOstcpcAkdGQKduMPc00CdsGbfjPyR07zIMPpcVu5e6GdomiDjFyF6S11Y37+qYVDKC8sGCpbD79pOn91s8ASZnDKFMamOUuWci5itx/kml/9ly6623TuH3vaqjjAwJLkaZp+GMjHWG4ThZo5tkyoTRPX5czuvSmQLt8Q/jdhenvOrfgTk3lm2XtNaFjZEmLzzCOPmti1f/+xPw1bC3vvWt06GdO7QRuhqm94/xwW2Z2hzuwqkLZ7q6D5d2k7oc23P8hJH/WPf7yHvfaURPpUt2TNdx3Xfe69LDzMMsZ30juZzrdifQyc7uzBrjOhAwAHM6U9c6pjypcp2OVacwunRWiSN+OjXXwvvtuu5sBFIHmLvGNdsncm+eg7DCcFZzvIipc7clyBMs9eKIETyP398fNKjpd1YlosubmGfgjNGT9qXO9u0ih7QZZ7bNpT6Tn3Ouye/aFhiTXys6N9988/TCs48BaLMp475kJeMop3Q35ZF74UiPyZX+hPyupZmyJf19ySxvaWsvJjm20mk/aU/JmxwmM2Q0yRTPb+1NmM/5nM+Z2EqL45e4zktOWDqDQ8LIZ117TxgyJA9phKO01Hd4xn8p72P3w1D5reJw6le9+uwwTlZvbT/1pTNjoPDhO2cjDZ8E9w5a6iptfh72NL/l61B3XGRRtw46ET1V99GZpbzGMkRW4TbFWUpnk588IqNwYxslJxnxzr3xPHkOf6QlvLOyRreHIGe+lGYmqR6ojDYP2eXLKVNkGTm6F/lcK6MjD4wSf0rkyP90snPkFXwsxUtDTnnWdSzr/OeDp46CEz7XSbvn0xEYO1GfTGVMxchal6LO+/u///sno9Z2C5+uNdHh5968416XTv23J0DnDXYGUXV2kZy9f+MrTf63CqMrbc85gzJ5DN4Mc0+zbdvxjtHYti/LIE0mcjvnWl+TQ63M+57ta2pzSHWIk0mOg0HLD2N5hlF4qmv/LJHxqH2aSIqvramT8E08503tb7znOhxyPUqfsElTXmSUv7o3ATZhszpJPn6RZ0znKlyHFaMbLxMddXTDDTdMbNRn6hcj7Shx5ny0cW7d/Xn40/5OfZKLDpIxsimH/JXFscmpd3qa1SfxpLlPJ02HvLhc40hu/Y7Jm1U053VffhSO89l5fZSPlOzbaQupb9eOtIuRJeYcdnHKh504ymgsdiSscPtmm7wv47mTnctYK5XpfgTGgc/gqIFqvK417nSi8Rc5cXIvnbGOo+58CKQTVjc+KWu7UjpqfkvOfV/YsgfdwGLA8HIr40envC7eUlr1246ANoGrNqINqYOL4CwPg6069r9oGBcZiNNencmjXecrZ/wYTM5c9Gy70p5vKGVKHzOe5Ure9Ff7NCrko61g6aztmLxg5MMKJjQYyltY4ThP+clhAsl4Fkd8bU24ONfKdZJOSCvxhE0fK53UUfjM005YZ9usrPiRy3tn/LBLGol7Vc7hmrN2oC59MEMdqi8Oo5Pqabyfukr97oNn6kldySvONd1KnsJx9FKbX3LK66FGjHFxwmBMeynuLn7Rq/DzW9shG130pUptg056D895yYnD+ZKlcmp76U+Xwp/GL+mRNRMd8pqA0YXog3sOfSpHnrDnT0ZjcuyllH2fXE9TvouMU8vvImk3r1MRSOeUxi4RA6MXrbk08DTgNHLxxOFc6zh0Xr5ClQ51utk/eyGQjhN/g9YnfdInTZxTf0uZqAeGly9gMYL9HwEdskEuHbzruv0R0A4y6GWQl3razb5yGtMbdYM+pP25dsSocS2s+66TBpm1Zff4043L4MgXuchDTkYeOflHd8lL7n05fORji5LJjqf+JjlWaNIfki19ony1SV+0e8tb3jIZcz5q4Ym0d7iEDevImDrL76Vz4slH2Tnl9juTVmHImzDk8+Se0W71l4EpDjlOeuF+SYZj9MMMf4e+0bY1q6FWvxjiWIf9pvInDWGE59RD9HJT3F3v6VMil/pU/wxs9Wx1Ku+TrdMrca1OWjERN+1/3/KO+eea7G9605smObUrH0L5jM/4jMlWyOrYnAeGZNaeyE1/k9487Gl/65/JFp7SwfH222+f9MBkx/hJRryETd2qb37iCsdmck4/FB07rWyHFq+TnUOrsSssbxqxZeM77rhj9ZrXvGYaAKwEGEB1imNDTkPXAekEvPTuRe4YBOn8991BXdUqCkdcDdDPeMYzTvzsqMFC3RkQPX3iGEY6aIc65VKv04/+ORMB7QhXnNUZY9PTY7zP06lDh/zlO7bX5Msv94UVLnH4u6Zf0YvEu+jzKDu5MsFgUJh82I6VSY8ypK/Zh5zSwuGee+5ZvfSlL702QVB/Ji/6Oi78+Iujjn3wgSHpoYLJT/6/EhkdXM7iKdsmJ13hhWWE06V8JIOhhgE5OGfc+Atr4nXXXXetbrvttumdLPH0B/oC/K6qw3JkZgJojMONU7/u+51w27BKvea8TZxdw9AtdUhG2yTVMT2zzZKuRDeX0lVuE50Y7pEz56U4Z/GTLv2Wry3UWMoba+9FkdsExkOEJWfikIm7crk+qb0spbPJj4y4JW22j+11JpFk896W/+8lf+GUJTKkL+VnQmSS5D1Y4bhddGeTjIdyr5OdQ6mpKyznaFhotAZ5DV5n74tdGrwBQYOfN+A0eEvRBnpPmEZ3Xh3pmMdVuQ5LnSnu6VQ3lV+cdNQJr2NPWuPZ/fzelGbvnUwgLBnAnq4z0H3tbN8u+SRdv3Ooy9QnA4mhlPaaMH5zwvEzcDvP23nSv6gzGeLIQodNNBhNDHkryGQmLxcDJHHOcpYfLvoykwtGT/o2xhqW8k6ewpo8CMNAe8pTnjJ99MFEh9zupx5GuZb8xvuucRAukxTGbeLpn0128vAi9etsQiMsTiZejky8hB/5zvM89t/hh4FDfeMVnR/rNXVwGZhEPmOtlQ7bk+mFd8is2ruvPJm0zWUW1vgu7nnXf7hirY2aPHhX1CRHeyCzw4RnnSwZp8TXrrRF9bTPT0NHTqzIGHbkzETMDgrh8ONG/XBNPm1OeE44/uJE16YbR/6nk50jr+BjKJ7GaQA0cN55553TsrHGq5FbqTFgjk8sUmYNOR2VjlYDT2cxNvTxOnHPeh7T1HlyZHCdM/kio7NyKldkHmXgl3hJa7x/Ga51qmQkq3I6lItbKhN/94VzXx2Ln6fB7vmdcOvSmAJc4T/4hdE2GMLaSqenfQZqBkpYb5PGtmFS/wmfOuQ/3puXQThHwmgbjvgnvX2d53Il33XpY0VmZ3F9Ll0f5KGLfskX5BhKKec+2crPpEbaL3zhC6ftNtqMvmPJCa/f+6Zv+qbpCbsn1frCxEkZUgfasbZ4EgPpCuMsPeX38MmTZn7SUGfuhVUML3kz3tyznU5cfgxIh/hX1akPnDAL23AOT/4mqlhx6+pKuPHYFPY0vCNX6pexb5KjP1H/6tYkwmRWHQsfPZvnp2zjtsakua5s8/in+R3O2iy9ZU+88Y1vnB5Y0Ef36eiSC1f15b047V0Z9+2kb8ULG20XS+3fQb642A7Cc7g5/HYIS2blyb0wThrHfF7uHY+5xC3bwREwUOtETXTsq/Vys0bKUNOINeA4jXjp9+g/3hfPvX26dJDpjMivg5Gve2TXseucHAYtYXSuXJ4OiSOss3jK6vc6o2afZThNWuRLJxqmysx/nRMuL1BjkvD8w0rcpLsunavsTz/oTIxHPOlTvhY0Z0PPrEBYIfUegJVRxsm+35eY15m65Rc9ye/Ur/NcV6IH/BkTzvQkOjMv22l/R1Zp61cYPLbhYLLktG3yM478HyArY7fccsv0/4BsNeEvzejzUhqn9YusWJCPgeWYs5unH376kPQr4pDRQY8419u61AfD1kMn8uAgDf2UfMLBWZvmT99wwloYPNPPqQNhr7JTfpzCDJtMAvHBkZ/7qb8lXu4LJy1nTnj++3BjOtK1OqffsfJgoqNf0hdF3+QZOeb5R05pjunOw+3zd1hY+bSNMrI559iUn/hx6mTfDofIqE/xvjG2Jj70YMxf3pu4Cau9jmnuW97LnF4nO5e5dirbNQIMOVvXNHAGmu03lrsvu2ME6DQNAjp+nY2OX8djAOKUyRKz+4wAkx/3HYw68dNBXfbynka+lDVx/VbmGGLx73mZAP2xpYneMDbpFb3Db8kJa0sTPfT1K0/jbSmSzkU69UwGcpLZ77jou/vK5bcJmqfGDBOyKuO+XPJ2ZrQw2PQ56/oYBhyZrYox2LVTRgjZvLfDkZ0j+1VxmKjPlDk6mN/ucwl3Vbjso5z0CUdnR9i61l+uc9Ht1EHO68Lv4i9t6ZFFu/HbpNd7L8Y0DwySv3QTfpc89hk23CJTZKePGWeT3z45Jc3TnHHV13kP1qHvqdudQCc7uzNrjAsm4KmfjodBkaeT6VgvWJStsksnmU6JQfTKV75yWpnSWem4dLY6WJ0vw03ZYtTx8xSPEfWiF71oujaYpIPeSogDCaRMY11ip/zOGcxTFGHDNn49f/CFZca5PeNhhxN9WnKMePetkHpwEN27iMnOWN9jXboe9TvXzuTThmwV8+Ujn+D1Xsy+t4zIi8GTvfpWvNbloU8ilzaOvThYatO4SyvteSznUn0ck58ya89c+jflDwP6qV0Lh2Hd9gQww47eGUPwjUt7ye+c067UCfZc6iJh9nWWrgkO+XwdUH9kFTnj3Xnlu4v80b/EIdN44BiWub7ecpNDXetr9E/ZAZIy9LwdgQ+1lu3CN1QJXDiBNHadqM7eIHkRhtlZCqpTNThZbrbN5VWvetX0HX6GmifAcQYhZVJGcXRm/Lyo6QmxFSz7/9PhOgub30nnUM/Kovw6c4OisjNkbQtiaGaQFqZumYB2YeJihYZu4bjJWdUxmaZD9E17iu5tirePe9Ff+S0Za/SBi2zKQj5fXvSgI19SXDcJOa2MkUt8RoU9/HjSvyXHPw8zPMnWXrHU5pWN8zt6e0xtdolH/HB0xI3X/PI754Tr+WQC9I3eedfO/4KxE0Cb2DRp9JDAl9DoZRz9jF7G76xnaapTW63ImHEs+fqtDQjn+jI6sjnGtnq95SWLunKQBc+2ndNpTyc7p+PWWBdIgGHG6NdxZ/sKI+iyNnodk6e99v37x5q233ixkAHl5UKrO5E9A8Mcp+X/V7/61de8dXTp9K55HsGFMsUoVLe2DZkgKr8XW8eBMcyOoNh7L4KVBfrliJ6s42Vlh5FEp/IklkB08bydwdokXvvNOwjyjIGR9s3PpJc+vP71r5/aj08UC2eSpIz7dFg4MJO2s2PUvzG/caKmLH7nECcykjdlG+Mf63XKm/Kl7Om/8jv3e96egHZjddOBJ5b0jJ7SwSVndcUOgfH+vtuOfMmQunXWztMPpS0Idx55L5V7nR85R0fW8XAv7fh6yxo5I3P45iFL7ve8HYFOdrbj1FDXkYCOU0PXYTs0/nQA11GstVnHaDcoeeLLoPQuReRmVOpQOWHTqRrA3EsZU2bhYohd5nKvBXLCDeXEwWSWIW5yyOnUswLhdzr7E5K7krdjWCh89AyvJRdDia55Opzwo0G0FG8fft5dY7SZyCQ/+ZPVJEFbjwHngYGHBXTi2c9+9vQ+jHKaqNnK4bwvJ93Igc9JLmHE4aK/yuCeA1/ndROmk/I4xPvRpcie39HF8Ip/wvV8MgFbOL23it3NN988PTjThrSZdY5eeuimLYU9v4w/6+Jt658+eWw/rtO23U97cO3e9XRhsE4G98mozaZM68JehH/kxTBtKOeLyP+Y8uhk55hq80jLouPU6GOY+a3DHhu9a8v56WShYGxwY4dxUUaIF749UbN32dK+/8EReWL8kGV8up2BYOxwYzAZnIR3T1lTpstU5ZGJfOrHkSd8ubckr3ILa+uaieFjHvOYqXzY8Fenyh4+S2lcdT98HKNbxxxPW9/yeViMY6SPbWpM6zTXyT/6Sr7os/RMWGJURAb3xVPXKZPVUP+ng25ISzsn/75d5Izc0h+vx/ziT146rhwpi3TI7pxyiLsv/ZWuI/KNeY0yjtfCxMAVl6z6JH2UMvgtDJe0/ea/5JTf/XBwHtOIf+Km7KM/P3nhRxccrvklfOJfpbPyO/DAAefbb799mugYS2xZNa54R8yEfxMrDxU8LLBCmvpdV6enYZy8R11xTdfkk1WI1Gl0bSmvlJUO0JOkvRT2tH7JQ3x5kDU66UxmMnrgZkuwLarqYcnpR/VF2OpLpb2pfEtpbOMnTXLGVsCWnyOMyB69SXmStt/CZRskmfOgKPET9pjPnewcc+0eSdkYQhp4DLQMiDoA98aGz8+h4eu4nP0WhnPm74gTZt5B5N5pzjpHA4zOJR8kYFgcuwtbHah95T4VjrPf6/gaMOwpv/vuu6cv1vmHhwZxn6UVR91wzvuup2Ovj3Xls4KWNuKsDjjX5+0YECYuPks76kbyduavrm1dNTAzPBh50Qf30p7PW9516adPotvzg5wO5cg1eYXbhwsHbPSF0g2TdXnw97CIc/Ywxmf8ySWNUb6kkfMmmdWXQxr0Ku9SkSd16prMXOrXb3nq17G0ddUKRN5PzL1NeR/rPbywN35gY0sv/X/Oc54zMc4kKLp1PTmoT7I6opfkd9DP1L1zwkYvluTWFzHqucRdCncWv+giHZNHZOdv2593GtO+9T3CLLmUx1inTRm3tPl9OnKkn5QfWbQ17YYeGCdNyHIvMpFBWHGVk/0RGyR8hb0MOrRPXpvS6mRnE53euxQENFqHRstpwH7rYDyZtLyvk+SXpxcasmtn8XQQOq50wCmYOPt2OiL5GfgNUjos+cao3Hd+lyU9rNMxZwDJ700yqidP7bHyKWRx5/GuWse8iddZ73logC+9pP/0lW7GCDhr+okv7THNXKtvda1OHeo7ThyyabPC+512rE1xwvO/ni4yR0bliOx4utbmY6yk7PuSmcGCoT4mskibHEtO/sJ70m+igzE//1vEU14yx61LI/edw18a4qqj1EvqiU6lHoWRrt9p2+J6KKQP92RcGsqF2VimMd+rcK3sWIWBvtGHbbzDaBXBCnjuY3gZHDnUrYNs6lD90zdGOZnVr3DRnbnc4tAH4YVL2XKehz/t76RHzuTjbHutbYIm3lbP7DAwgdGOl5zyKYty0eF5vS3F2dVPu5E/JvLSdmxJZPOYZPnN3338lIMfp3yu1Yk4dCdsxUnZd5XpUMN/qIc71BJU7qMnoMFquBqoDsYkR4fkizSexHhioVPQqHNOo0/nC5IOwoAhLU565+HkreNzyMPgz+/YXcro7Om9F8rzf1/WlR0fxlcGRQaZAU8aSW9d3PqfjoD24yk8vozLDJinS237WPKTlzbMpY5j1NGF1Llw2nLacwwT/sKkDW+f+/mEJAf5ycXpj/Kent/jvX1JIE+HfsVT/7zHQYbIMc9LP+h/FFlBZTw99alPnfpCfvM4KdNYH/P0ck9Y9eE3Y4uL0aXsZAyDhBGe8UUPfXxCX+HDGtq+ibjwV93hpl4wM6EdVw3UJf8412k38buoc/KlB+RSd/wc2oL/6aUc9My9cTyeyygN/dK6ycU8/D5+kxM/+simMPb4X1lWoB0mPepiyaXsysTR3fgthT+tX9oYjpiS04qOfI2vdo+QUTlSB/ISL/2nPml8IHEecp62fBcVr5OdiyLdfE5NIB2SzpJR7FPOb37zm6fB8dZbb51e1vR00iCrgWv4eeriN6cj0CnozPLb+Twavc5auvJO5xN5psyP9I/6UWZPj5Rbmflt4qxe1JdDPIOdDppzT3rOm9KYbvbP1gTwNXAyogyCnvgxOj3J3JdTZ455+6IX0Y/cS7i0VbKl3t2jQ2R2JM6+5DxtOimfM7nIG5YeqjCSuPQDrtMWTpvnGE9+tvkxIp3lgxt5lhxDRx0zyJ72tKdNDyJ8LEJ96K/SZ4qbNDaxds8RDtqt9DyA0kcrqzylTS7pR774m3jRBf/PyOHrk9LUb6TfXCrLVfDDCAu65RrnMHeOC//RL/cu8hz5yGuVzgNIH+ihC8Zdq1N0wpF2PpdPndORjOPz+/v4HTmdyRLdNHkw2SaribcJj7biyLavpfxx14+mD6Dn6mtfDit5SBNLH2wJU3JpNz5WkXBju0kZ3dPHezCiPPyvoutk5yrW+oGVWWPXQA2cBne/NVpbnryo6cj2B53OksuTG52RMNKIk/b4O/5nOetIdTzS1VGNndBZ0r3scZUb3xg2fnObOlhhDRgGOZwYO0tx9l1HUyZX9A/OBk0GqjZlC8emQX0fmNTfWId0I3oRYzu/x/qnF/zJ7OD2aVCcpmxkT3nI5iEKA49hEWOJTruXsKfJZylODBufG2fs2OIkH/7r+j9hsbPdRn9JNkZp+sJ5vch39FuSI2GESzr+N1Hex6JPJjPad2SLIWtVxyo7Q034sc8gZ/qNdfkes7/yY4odTqkHDNUzl7N7uX89mCRvZzIZo63m6Fe0CQ9Q1PGnf/qnT3JueuinfLa73XPPPVNaOGQcST5nLeOYTtqlfOjf05/+9OmdMQ8FcOeEH+OM+acOxHdwGbvGcGe5lgfZpI+razw9XMBLG2ML4cQJH3nHa/UirHRceziccGeR75DiLluGh1SCynr0BAyQGrkOyFPTz//8z59+60zHjmZs8KCkMWv0Dk74/M79nPcFUqeiI9KZOlyn0x7zHvN17V78xImRl4F/vJey7kvmfaQT+VJGabqO/Et5uK+cjF3xDRauUz4sx3RzvZTWVfXDLFyccx3+4RJ/bQlf2wfxtwrB8DVoJkzinPY8yiEPv53n7SK6QSZunr84nPtjfDrCYN+nIxvHGPCk1wQhfvN80q7JIOxdd901/dPgW265ZZpQkFfceXnm6Zzmt7ojo7RttXn0ox89JcNf/7bk3LNdzOoTdpF/XfmkkXpbSi/3paP9St9TcTye/OQnT1HCIHWYPPnbjuNFcGfOPeESdvK8on/UKx7aowMTzPipX+cwc8Y/fnNk0nJII3Xt976dNMlqTGaU00kTX/7yNXZrT9y6/ONPVtf5vW9Zkx5m2GF74403Tg8p3CMvPQ5vur3kyEdW/W8mOfuWOTJqJ+TygNc/VvZwKm2HfORY58RzP+OqB0Vh7N463VmX3qH6d7JzqDV3BeW2zKwDtX/ZkyMN9TI6hkgGetfpLHWI/DmyO/zW4brnzC8dp/24x+50tBgYJJRfh5wBAwu/8xQ//sfOZNfyMYBsZTIAujZBpEPYjYMgfg57vq3mWNnx9TsDvS0O6wzlXeWZhx/rLTIIQ7YMuvmtzrUX4dzz25ls/OkIudNG5nmd5XfaqYmfiWAmgEtppq0yimyppccmE74mpi5iQKSM0hg5LKW5D7/ku4+0TpOG/CNDzhhw+Y3DGO40+RxznOi+M/130H+6Fh31mz+X9rLEhJ7iP/IWL3WxFGcXP2lFTv2Nw6THF8K0BZMf+QuTcPvKexc5zzNs2nj0fJ95hZttgB4m5IHCPvO4Kml1snNVavrAy2nZlnvsYx877adlUKSzv2xF0+kZZAxCDHlPtRhPvgbHcM/7RQYs95VD2HHgYGi97nWvWz3/+c+/bMXbqzzjQJiE08FncORvgEzYhOv5gwToiqepJtbZG0/P5u0jXE2KfMnHk1ZbiBjpJkj7HqzlPzdsIkPOqVO/Xact+J242oYJDrl9nthqhi0+jL99OXmn/FgwKsaXwuf5RD6yMerI6v8BMfKwT3nES7r8zttdRB6byoADGSLH/Dp16pzrTeldxXuYaQc5MKBDJhIZV7Bzn79zeM95GV84YeKij/l9lnPqUDsgQ77uZ4VTm80XwJJnzmfJ86LjrpN5ZC6MA+cw2Yec0lTvHu6Erb6M8glVAAAgAElEQVSvbncCnezszqwxLpiADltn6swQyVPVdOQXLM6J2emYTGQ4+/htvbPVxRN0e5it2LifyY6zTlK5PBXzWzx7/6+C05lz6lY9M96Vn+HoN5fBPb8nz/6ZCJg82zaSrRiMbTpInzJQG5hzeIncxIiuMerTjvY5SI9VE6NgNAiWjILIl7h+k4l8XszVLvw+6Qt/ib/LOTKSCxcrXp/6qZ+6Ngn8Mqnx9Fr7NtEMb+k4pHuVdDblXwuuN7YmQHfovoMO5YFEtorx0/bTLpYSNuGwkuuB23nUjTTJqT3ob9IGnLOqo80K5zi2tqDsyjceS/VwWj/p68ulHzdex6/nkwl0snMyo4a4zgTSUer0NXSdOwPZ+TK6GHI6e4MNQ8hTGYalp9K+9MKRfzRKDRYZ0JzFOXaXunXGzYckrDp4iu9Fan6c+zr+ugcS0BaydeQRj3jEZBxpJ9jhxmGXw4qFbWsMlBhSwtK/fbux3lLHVmntN6fj8iWXc9o2g8hv4chEVuG9iO+ppnZD7n07cpBB/pkw+r3k0he5F1mETVnCfSnusfvNy57f2LjOOf7HzuO05aNPo07Rfe9c+SfM2oD2a3XTed1Y6J44aedk0bb2NelQl1zO0tZmPbBKO9KW0qb3le9pmZ4mXsq2FJcOR483hVuKu60fpo7UMZuhbncC+x8xdpehMUpgIwENXUeSjlTH7UgnszHydbipszfJsZffSo6tQgYtMuuoDFDKQ35nnVgGAWUU1pOxq9KppZyYGcgdBnZMsMAJ04S7DlV6qbNMe8DHdQwk57lLO6Jn4WqyFL2bhz/Lb3k54ui5Saz3hbSNUVayODhyC8tQ8zliDwue97znTS/nWvEzScoEL2mf9Zy8I0c4jfKPeUQv3aenZHV40p40hHffb+VR3roS2IbAqHd03UMgn3LWbrRVq7heVjeRcH+prcvHis6b3vSm+63srAu7jVzzMOk3Igc95zKe6bfpvzzHMs3Tucy/lWHJKTvnvnLn91LYs/hJ1xF+3cZ2OprtfU/HrbEukIBG7sl1jAidC4OHPwMiHasOwTV/YeP8dnAxUoQ9rw6YrAwf29D88z4TF0+nyTAONGSMX+TNWTmU0/3IOoZP2S7TOR0ymcnvd/zWySmswRov/xwRK5+kZbi7xkAdG0zDZl1aV9kfR3zC22/HkhMuOuq+OFllOQ/G0iRLJjfyTnvmN8pMF/ilfWsvz3jGMybjzva1tN91ZVsq7zZ+0oscwkfv1sUVlizOXMqTeMrgmhFEl9NHrUtvF//kObJwfZJTRlzJ6toKqokkg3gsyzZsoyfJN3Ws/lw7ck96WPgdv5wTluz6AEa98u2T10lcLuN9XBi1WOBy++23T2z0iXYH6CNNeDw4E3ZdnXmAhKl3Z4Tjwn4f5U5amXCptxjjrvmTTTg6oB9f55RVGOV1nbTXlW1dOif5k0874FyTSV7RRXn7RLvPYGu7yrDktHH3hLOLw7uP5Oe/TydNMuUdxfQnuKSdkF045YifOOO18OQVThpXze23Vq4avZb3QgikkTIcdFIaqw7Rb52V3+m8+MXAIJxOQKN3SMdZh5COVJj47asw5NEx2bbm5WUdDjnkf8wuHauy+iCDjjXlXld29SCsp48GZS95+xSyF+7rzodA2o76Ui/aC51VV+ftGGq2J/p8atqh/F2ThRwxFhhqDHEGucF5nQ7tU2Z5OCKDvmHJRWb3yDwaaInDiEqbED5pLqW3i1+4pb7IK32/N+VhWyDnrH1ZJYihx3/ON213STYyuD/KIJx+OGWWHhbCCM9hFXn5+cKmMN5rfM1rXjN9kEUZ9B1X0SDDKLqFAza2oWGRT3pjg2HYT2Cv0x/yRZbog9+cus5DAOFirK+TW3k90LA6SofEiZ4lzX0Uc2wjZJGP9isP11afjUX5VHbazTzvlEN42/aE26ecyQ/DTBIjr7xs7fUQVV9KZ+Qd3RFXWBz50SFl9NvhnvBpl8nrmM+d7Bxz7R5J2XTuXBqzhu/wW+dkwqPRatQasU7W7zR0v3PoJMQR97wcGXTY8nA+7/zOqxxnSZeRahDAXT2s61TVo6di6sVA54mld5U62TkL/c1x6SeddFYv9DSD4OaY+7nLIGZIxOggS/RDGyYLP7pDPwz2wp5nm03JMOFyjly5nzP5uPAjGxmVTdwYHfz9VqZ9OWkm3VxLX56YLTmyYakv9VVIZ22OAeqe8jjv4pTLQYZwSDn5cZEvv4VzyEtcBhiDzUv0JreMemkIc5Vd2gRG6tUuASs5DNxxlcb96+lSv9Eh9ab+/HZ2mDgwtlPfxsQlp2zGDGMHPQ6D6M5SnNP4SY8sztFHZ23CaqeVGitowpBlnSNf0hIm5V0X/jT+8uDwIB+ZXGs3ZKMLdkSk3YeZOK7VA/3B3xdsOW0ssl+ldrZb7zah6p8SuFgCGmY6Etcauk7Jf1pmKHvHQ6MdG7fGn0atseuUvCtgtcXv0e27wZNVmvIxESOX3zqqY3Z5coS1T4TfeuutkzGlHtaVHStf2rr77runMPk/JcfM6XqXLQY5OaKnaSPnLZu2kPYgL9dxcx1xj1xpO66FoV+O83LJdy7PmB+95Rgg5AtTBpv3ikzQTCb0Q+4n/JjGWa7JqL0xDvV/eGQCsZSue/pK730wkrxL6D/Gm2RsireUFj/545P68Fu6ODiTx+Qq9YcDBsLHAGMEv+IVr5g+8W3F75nPfOa1+Hmqvi7/Y/bHKXpFd7B57nOfO62CYYtldBPnXF9PJmSIXGSiD1Y7rNjp/xnkJhGbZFVmE17tho6k3Yvjel+OTmJMTrK51pbsLvCQjZ9VNJ/P9jEXsqxzZPPPccXT5pP2uvCn8ZcmtuTFhu3z2te+dpLZ1jntiJ0R7mGlDtLWxMNXWpwwacPiXQW3vhavQulbxoMgoBNhQOiQdETf+q3fOv0PGh0No1rH5GmRhsxPx5BOLB2Fs4bvns5tdBp9OojR/7TX8uDI4PBb/vvM47SynWe8GDfqyRNj29E8Idvk1BcjTLgYSeq77vwIZJCjjwZK+9NtJfTk+LydgTWDMjkcHN3RTuiD9uns4IRxL2HPY3BOftLWT5Bnm3zE08aF9Y+OPVAx+dAvccqScu67/TNwrNKM/Y22t+RsF/M/ijzdtXr67Gc/ezJGPRkm+1hW8pJ19Jun6Z4wKZu26+nxXXfdNbVn93EhT9IR3m/tW7w77rhjavO2rt50002rO++8c8pGOGUS/6o6eoODAwfMMm7hSUedcQzf68kq7YdcDGuTFp+49yDLFyK1DWOgstCVdc4EiY5IT9m5fZePDNLnnE0CyImvh6Hk1V4w9/DtJGcngjGMU8bU00nxtrkfHdAf4WLrqW29dkEYYz0g8JVKesA5h5tr9UEm7ZwN5R7+4u5Tzm3Kcr3DdLJzvWug+W9FQMPUMWnoGqwniFna9z8xRgM5EwudpDgavQbOsGMciJ/Obt8daQqT9OV11TqVlD0sNjFOHWGUOr5qvMLpos7qB3eDpyeSVgcM1pvqaV+ypT2o4+SXgXo0Qtw3UMeoE9YhPpc4+5Ir6WOj/2AAnZRPykIWkwiGmn5G3+ThC9k5Zdm3vEnXCgjjjNxhNmU6+0Mm/7fKio5JLaNOf0iu6EOi8Avn+K07C5t6EUceDDF+8mT48g8rOqeexcs7jR6K+Bw/P2XYdqK5TqZD9x8NZkw4HPHksOXcm9fddOMC/0SW6B55GNVkY2BblTI+m1zTjbGNz8U0ebel0QqLcJx0HGlL8zj7+G1iTT+t4jjIr/2f1AeQS7zIiMW+5Uza2o1+Wn7ajf4lbQqDyOHs4FI3ftMdh+vrrTP7qLPTpNHJzmmoNc6FEjAo60QMAp5AP//5z59WDQwAnMbLpfNJY+enwfvtnEYuXK6FGcNPCZ3xj/RiMOkwI5cBIR3QmMUoy9L9ud8YfkznMlwru7oK75R9XobIitMYXtkMPs6j44df3QMJYIszRniqgwzUDwz9wTYhHMNCWIOgp5OeZp6HG/WVnGObiF7E4JA/P/I5hHfwcwjn2LdRId/oHPkYFlZpIt+ci7Ax8IRloDHmrJqIE4NfOIz3qbvSdHjAY6Lj6a485YPVksMrT3bFMykTHsulONJfV/awEiYuOsRY9M9YpZ3VOumoSzIkXfnTPxNEYf0WniPTpryT57GelR0n9eKMG+OfXuLIOeMm7EmsEuakcKfhmfp0dpjgGKPppU9jkz3GuetNbTfGuEmPQ5lTxtPIthQnuo5FZBfOhNvqIhlt7aSLDuHXcRNWGpzzprBLsmzjp/wOkx12UCaPtrL5HX2IHOtkpTvaGJcJp7Di77Nv2qZM1ytMJzvXi3zz3ZqATseyuEbpP8X7nLOtNzoljfykhj5mJKxGnmO8t69rHXqeTKUzGg0o2z044ZRJGAaIczofhokyRl7h05GlvPuSd5/pjFzH63V5CGOQcBg8dOwGOhz4ZbBzrlsmQI+s0OScQZrxsOQYI69//eunbUe33XbbtA1U+9qmvpbSW+cnPW4803f1PA6w6nZev+47+Ofa4G7AphtWUmzF2KeLnFh410AbJOs6Rz/J4H0zRvvNN988fU3QxIfbN8/IETmd1XXqec4w4XPWJyVu/HIe+5Rt5E466obeceTQj5k4u++edNOH8cu1e+OkK/ciz1U+h0X0np7hhi8/v7UD/SS/jCPrmAlv/Ek9Sf88HP0jp4m+yYOHJ8YwhrpjXO1cyl9cThmT1r5llV74jjLYRp1JADnSlsbrMXyu3Zdewu9b3uSjn2H7WCUjK67qdcxvvE4858joWhhH/NbFGeMfy/X6nvxYSthyHDyBNEiDo88sphPVYC+70wkyznROnsaYoJnsZACKYZqnRPyVi2HnZeer4NLxKqvyxxjOAMLf9bxzvwpstikjo8fqAp3RRugUg4GBseRMFIRnlHi3RJsymO67PY31Gjn4aQ/OjrGOc0/9p30om4Oxpu2YqBn09z3RIV/6GewYZvqZUb6UwTn+DCTMfU4by6zoJC1hl8o6pnU9r8mZI3KQt+76EaD70S9S+B0dyj06pw0Ip/7W1Rld1p7oqfO+XfQ88mk3XprXRvU//MnMJey+ZdhHepF/TGveLsZ7rkfmS/Hn4U/72yRVPWOr3vWfdbsT2L/27y5DY5TARgI6HQ1eh6Kxa/gxmDZGvE43DSqMM3KS2eTGk3d+ngDr/B1+O+KENTgpK8OVkXfsDiODNh7KrK7Vsd/uOXOYnMdgfQx8Y5wztD3187QXq3WDIr2ytYRRwqAXbtTDfTGhz3ODQX06cm/MS1j+c0dG79pZabFNhi7wOw9HBmlbPfY1piV5ki/GwnvKbkuW92eEp7f8uU3xk871PJMzx1wOsqcc83v9fX4EtOe4sa241lbThkwmPNjgN8ZJXGerlMKpRxOe83b6HvloC9pr+iBt4rK7sa2mTTiP/mMZ0jbGsOP9fV6TwaHvC9N9pn8V0upk5yrU8oGXMR2lRs4o0+C5+F+24qUT9AUaX6TxUQWGkT3MvpziZVyyG4QySOnIlI2h79qTdytBx+7UaTpyA6WB3OdxbQXKP2TFgH/dMgE644uEvmrlox10DdPo4TyWL/qYFNFBhkmMqHm4ffwe5YiR9oGf/Id4Mb5S/+QVRjtwTjvXDvIVsac97WnTRM3vbb6UtG0ZIgN9xMVWLO8drGNIvvQ/DDsrt+R1iJP0xvJvK8tFhhvlvMh8m9dmAvSLHjm0Zwc/eq/9akN5t0R7WaenHmx4QMC51u7pqPT24aLf0XltgpxkMr7Ji1/yS/h95H2eaYztIu18U36pq01hTnsPOzJkrDTBrdudwH40fvd8G6MEtiagkTOM8hRLRJOEdR381gmfY0CDkX3/nqAbYGxzcfYSMyNNBxbDyuCgPBm0XBsoMkCco5iXImnlZrAbjE10bFWyyoNLBhpMxt+XQvBLIgSDQvuwzcHqzkltgxHvU6sY46tdib/v9jQ3ANSfVU4Tef9zI4M4jGkL4pBJmeiF92Fe/epXr17wghdML74LJ8y+V3aSLlmkj+EmF70URrm0VwYSjs5cznMOm9K96HujUZe8ycvlHP+eL44AfaSD2og6skJj9VC7dU3/jSNWxfWbwi85bch2aOfo7Em6vZTOSX5k1A7iIg8dSr7/n70765EmuQo+/nwDsECvwAgY72b28XjfGGwMGIF8wYflBi7AtmQ8eGHG23jGCxgwILgDictXvzT/mXBOZvXT3Vnd1VV5pKjIjDwRceJscSJyKTinqlPRicbAcamyMe+acRuvpGzLMWqvdse+9+Prc2Bf7FyfZ3uNO+YARw04fo4kZ8IRnCKgzwRjt/eJJ56Y7uj4tC/6pSab8sYjUOLYnMNrkjjFMW5Jk3FLHnvAN2MXkFsAjbuQ8WnLvs+hLXrEFlogpFdr9mEh7ho+m6jZl3xrfZvLS58CNTvNZA3QCk//cjRIaILvi2hsyGNlvfgOz+Jiyx1OvNAfOvDR8Zz+UVfgxTN1g+qoH1TW+Snl6BxpRdsp03tKvDsmLdkBWdB1d3TYgnnEIscjll5WZwPjQmZOk8emzSk2GbJv56POzuvc5JwOsQfApkv1mb3km27Sx7HrjHqfXcj5gyWA37gbn3zLMepDe+RF1vi5Rs8SjXvZWxx4y0u/VbYf7Rw4KQ54vImzlxxz7pyAxPjloDxHFU658pzvOEAOaql8xLnOsX4E777OJNl9s/BRPoLzkbbxGgfXtegLf0taxz63Oka3oNbjFt01mI+9vvDJ+xj+jBC+Sdzne1v0aQvgx1obtXXJOd40KaYn8W7OF/qE702a413ELXkcHeUmbIGaxYtPFCsvRQ/a4Cm38LVr3ccC6ITr0jGgvvEx3qz1Ey48d8jG987Up/eNTRtoV74FaJcP0F7Hj9MuWtGNNu8Z+Rd2tkf+2oqv2gTOD/maxgRHHe07ltStHW2li8o6rpzsBeXu6rpjsRWfpkE8wJ/4mrzMd9/73vcmHfLiP3uIz3jHXkaejkPWBt3kj7ULtuRv/crRBPRD/hLdUk7nnB/qOzw6MupJfUyN3/JHW2hCD8DbjvWPRraBX+5Ad+dsqVu4wJMINm/8h9WxgBwB3pI5/sTnytEz6kI8jJ94r462tHFpsC92Lk3iD3C8nI9FDifvPRjAcAVCAiK7VgIOhszYAcPn2OSMPVxtdW1CHCbizm+bcybenfDYmvdzclS3bffU68dX/PaehfeVgElkbcIiR7gmC7zy7on/EjCB7HA8DpAVMOmRTZPg8Xr8RcvuzljMSi1q6As9QJPkWJnNDe8l+LjHXQA+6Dc65Gt6m5+BLyDiVwROFnPKHNP7Aqi1dm46Ln2QWe06l9YArqAOXe4Q4DHfyafGe7SC2lxrK5x4oG1Al/i6+Kad6KqsNutDnzY5+HVBKCgP99JyPME3PDJvuZvj8Wf/X+Qcr+LfffOGXNGLnjHPhukXnXA32bttjl1bAmOTaqe24W45Xu2nj6PN0DubkuYtOg3H47ZroK62+Cd0m7vWxrbWxlXl2Q/aJHxAF39jznzttdemJtg1SA7qwUOPsdAhj0E6ZrfZ7Nb0XjWe+7y+L3buk/t734/FAY8zWcxwmCZskyrj9V8hjF5QxIA5nIx7NPQcmndofIGq8zrf0pFqU3voQAOaL2Wxg6+cP/l4V8nL5BapTV7xe8zxiVzwCd+824RvOxyPA3hOVk3oesLzre1gaQT60be+6AXoHF2Vh+faXQMaomOt72iOvnScDxKMtvuuHXxmE1tBtMndEeEL9Y9/a6B/uGwN+Ny4/0JxZ8c1/D5Uf94ufH2WdwyvoIztt/hxXcIL/bB3AZo7ujaGvGtmk6NPd8fXeb+XcE6ueINPkjnrk5/85HTXy90G8sb3AP59wdg3mvIp5OdYgO2YX3fXLpwlei2+JfbTnDm2v1TnpmXalYon0GXhYOFNf/H7M5/5zPQJ7RYSS30ZozoWRTY94G5p6/pkN+Kb7Mki5+WXX574pH+AZiAegg+MKZvjlyzklGXv6uJB+FOlM/7ZFztnLNxzGRpjHCdNOykmbYbNWQksOAIJwOUc1GPcErCrfBcwdybO0RMdd0HDffRhUjNGDp9M3vWud00TnHJpCZRzxCZFOeebA1/C38tuzwEywmc6yVYEnuPO+u17WG+BTepXCtASNPHKx/KuHzvXp74L/Nf0Fg/hwHUs0AH02ALCYh9va29LurMxixf94SVa+L+Cnnl/7pp6uV3AY1HhnTg2KnC6KZ+zUzxg8zad3KXlZ13jm/EgWeqnc77b3Vt37vw/kS8J9tVK47kpTfNxP9Rz8sQD+icnK4B/UpB+3he/6pdOArJGk3OPgnn8jl83nja0wm0M5dkTXWVPzgF87W4FaI5ubbIZuidXbt5q4eL66KtGGozT3O4JDvjOyUbZlqBd42dT7AWteGmT4KWXXnr0sY99bOKxMjYXr+Jb9f76r/96eg/WOOFcmp29NeNsKZ29rZ0DG3KAcXJ8DPnHP/7x9IKz4MzOpLsHksmAUwCMPIfmWNKG+oKD0dHBV29edhvyOXcOhkPh+BwLBnLet2n7lOuOk0KONnoPjb16+DRO5NXd8205gM/0XW7yFPCaQJ977rltO1poja3RDX2Tu3PHbAVNzh1nt/K7An1HDz3U95pfcI1Ou+64xaIAT9DRGBrnlmPQZ31Hb3zS3xKgD3hXyovtPvjAFzbmcZzaSh5LbSmD39i1wb9ZfLnzYAcfHRZf+b1krG0+kY+0KPT+Fnr4cvTAv3TAq/xlcsavFjxkk34lq/viGdmnB+mEx8o9Kvmtb31rWlh7b/VLX/rSRCJ64S2BMfp4yT/+4z9OenCsYFz/0Y3X+mW3Tz311HQHyrEydnyI3mTAV4gvtNmG69L4blKGVjRqv9gFXzzSSDc8GohG/dZ3/G2Mrrtj6roykF65ZhyXAPti5xKk/MDHyDAlt7g5Qi+x2wlkpO2q2FnJcDmHDD5D9hicSRaeshwB1ozHW7BKP5LdS44QPQV2W7R/qm2YIDhUY43vySEnu0S7AKfgkpx3OC4H6CZ52IUXcNJTMmAbxwb9sodsNP2gL+w3PVHetWPTVPv6Q0PBC312vgTR67qxuEuhrH+P99hOwakxSdnEUnvXKUOntsirR5yqf4je6OAz2ShAu/KR18q0P5bVfjmcfBo8di+gckfrgx/84OSv+5y869KIzx/z5zag7ORrDw77d2wcl+oL8AGkh+lNfCEvkE6FPxXe8c/Yt2NydQfR0xcW1mRu8esaOY/4c1KNlx9S15gbd+Od49/0HA3pPL1lDz78YLMHvRZpFhF0kw+gx4dAHbpam4dwb3INH7RtEaafT33qU9Njc2hTzp8DNmNs8dh5PFSvduiRsYGuTydn/rMvds5cwOcwPIZqZ4Mj5FgsdjhVu0CMPcjIM+DO4YS3FAyEXzu3zdGpP+1KjpXp2zgkwLl3Ha3KOVY5x9Y1OWg82sGTU4McaIFLk3P0L9ELx1jIFeCJ8/LqGDM+nuK4o/G+cnyxq05n+poVvipfAosbye6ryf6ZZ56ZAkyTfjq2VO+6ZfO26EGBgX7TE2XkCz+b0Bf6kztc9SXH0tagf7SgAW8sJtLpeV/oAvjteX0BmheU3TFxt4y9s2NtluZt3Oa88cc7bcWftXaNC378g4+28uo5B/jv+hKwQ9ezVXUEiBY87tTU7qiDymqT//aOhLuK6tIHeXoQDUt9n3uZsWcHbUwYM7nhHxnSL7wfebrGF/Xi6xrObcvZCdrc1dGXxb7k0UZjSF/W9En/xi3B0YbU+W3pq37659wxPvOFHr2M1/gb0Ms1mtUH6KzdNdzau0lePz5S4S4Z2etHHtR/5/KRFsf0AD/zGY7j8VjvXI/fkuq5jnAf14PnAIfEWE2mPu8o56AY7ykCB4k+Oy85a07FxG6B5vY42qWCD3jOmxS8hGrn8xwgZ700FuN2HX+MXcI7k6cyDn0MhJba2MseTQG24Nq7bHQKH9fAo0bf/va3p8XRRz/60WnzQBm9PDaQ6ZI+sG8J3XKQPjh2l8SjWB63688Ut6Y1Giwa/Znpz372s9Uu4BqLzQlfb6LHvjDnzobFzqkCnqYfxpDtrcnk2ONI1ng56kblx+7/FNsnC/okZQOOx42M5Ih+84brS1A7yRkOPqu/JaQ/NkzcbTRP6zs5yjvest9LaAsfLcT4mkMbMJfAi9uMcV/s3IZ7e9074QBj50wZu90iufNTdZ5oM5mg00QkkBQQCaIERByWIN6kI6h3LABRTwJ2Pg8FW3fC+DvoJF5Z0Aq2c+wtcE9VxnfAmsfuwuLQnR261ILZMR4ugZfU6ac7pF7GdZwOLuHftIxsR/nRd/QV1Lo24lSuTAqXHbEFj915RMbdE7pijFuBvgMLls9//vPTu4Dscgkal/yrX/3qRJ/3Tk4V8DMwVgl/QXLo+ohb2V3l+o63d9XnqfWDB/wgYMPkJDd/2NAA7N3m2fiu6nRh9qNOG4Px9RjyRaOEHnZpseMuT+WRRe8aW2V7fpgD8UzcwBfucDMOLHvym7W119o5cBQOcI6cpoBszE/Vabqjw+GbjHweW6Dmdr5nbX3Ssq/CGYtgykRm56bg1LgEdia0c4Am2aWxFHgZMx6YzN39ev3116c7eMp2OMwB+vT8889PiwBf2bJ4OWQb7v78/d///RTwumsm+KGz6d/h3q5/NfkXZJE5W0YnG0Cra2wBbvjO2RF98E6Mr4h5od2dnXCuT81yDe2hAT2O7aJb9KwtdsZWCkLkj4M/1r2rY2OSjA//AVqlub7AuyuIFjREi77Tlbui45T6yXbJKvtQxhbYjccmbYbZRBP8sts1fvGnPSqYXPF6a6jt9B89EtqiL5yt+z739pJtfpIO7HB9DuyLnevzbK9xxxxoQmTsJSRUfsfkXNmdycRk5Mtxbuuj0wcVlJuw5tEMfDIAACAASURBVLszykwE8sCkcazgsz5OITduE7Lx4ovH9/yTusVeL2CiM4d/CjSfGg34hz94yT7k0hrgMzz8BRaUo+6t1bttecGPhb8FDJmzDbS65lxwV7nFvkfXbBj4PLF3YoDrWy+C4188tAjUj/IlQHdBIztFK5tX51TBWMgd3VJ8XhtjPLmL8egrOsrvot9T7SN+NGfQSzrW3y6QnU8P00N6t2bvbFw99n2M+UT/o88ZbcY1gLboKz9Vvp8iXXQAj3e4HQdO1zPfblx77TPiAMffBM1hN1Gf6hA5ee/beHzAY0L+wM9jN8oFc8bD6Ts2FuXyJjiOTZl0DmAcxrYGdsSBl8IFsXjhcUUvO58LD9bGvkX5GEyMfF7jncWGOgIgwZDAHmw9oUZLAY7z7tL0blGBUjvY2QRcizh3oNDps7AWPOrBWRvbTfmpv2zSzik/U9lSm66hQR2Lx1Ne5KA/fiVjvKUH42NOXUteS+Peuiz/hx7+cly4b93XQ2yPLNiouzjf+c53pq8n8o0f+chHpg00j42xhzWwELJ5ZNMArwFd6Hit3uOWj7qiXXYBsme2yzZGvMdte8f7BQfwVeKT5Ftv9FwKn/fFzqVI+gGPk2PmPDl9E3KOmuGDzgtO5o618xzwnBXaaaKfX7vJuf58OcWnLH2GFV0+mT3vI7qUN0mU59DgRF/jm7dzExqPUQd/yQJ9gih/KGeykxrXvF8LHY9l+DKTxY7HsQS1Fotzuc7r7udvcQB/5zxe0xPyoF8CS4GI4L5gfd7GWz1c/4juStqUk6fPz/pal3fX0Edn0pvGgD46LxinByZ5Lz0DuCDbn042+EGbNuV4Ec1r/MA7gSboXbPoN67GvVb/tiSjM5rj86E20WR8FrbwPdpUEKxebY1twFsD49JmufqO0yMyI0dtzPUreuO3PtzR9bgvOWuDnLV/yYBPeOCjHPzjs88+Oz3Kic8eXfU4p4/1HAJ3dSyU6GtwSK7hXDdHZzqEPsfkaM72dIPr2Tq9WILoUr+xw+t8qc51y7SLF9HAdtGKtvo0d7366quTPlpY0uUlUM81/38DPve5z03tKN8a8AAPiwvwli13jvY5n5QB9UD2iObG2rUJ4cx/9sXOmQv4HIbHETFqxs1QTZ4Mm8HncFw3eeZUjds1eBKAU90cgfLxeEK85Q8axnSMPm5J4lGqkwcgL4+h5fTxfc2pko3ACz4875wIiM/lS3RHYfQtG2VDdnzZi7sS5JXt3LLpK6u7W+c/LfwHR0AHssHxWJAEzyL4viC65v13N5I/wUMJ7fiIn4A+54Ocr7U1b/uqc32U6lMuZXPzNtifa+Rul1/gI+hD91od7V1FMxzjpVNoKqjOF6DDce3AQYt6+OPco1ndZcJPbaz5i/m4zvEcbwL8wAsbQDYI8AavyEwKN/5W765y/etbTpbyaKIX5uzm6WimK0sAj05Io/zH46V6NymLbm3rV3Lsowo+goLvLYgcL4FyY2/8tbmEe9MybUYffpI/30MHLGL1baPAtfifXqjr2DXzaX8cTSZAueuXAvti51Ik/YDHyaAB4wWcEkfjjgADZ+wcpOtdkzeZMmrJS+9ePK6dqbENg5Da07eUc4+ueb/hn1tu7CYKu46OyQ//l4Dj9fiKBQ552UkrkFzC38tuzwHywOvsIhmtBSG37/GtFtirCZv9msTZhLKO0eRYGRzpFCGfhE5QXnAR3en+MYIKbedj0ICX0bXEM3LmKy12LCTpgLtT8d71EYxpje760efo18hWPW0Cx3DDCZ+c6Zvg0maHRRhf0O7zWr8jfed6HL/IA58sSP2/ioW/LymSIRw8ksfj++CH/kG+xHFlcr7d3RMLCHMvu+iO6JxeuHTB3ShjoivaKJ/j3/S8NtXH4/TeotuHUCwMfFnRe7bmo3R33l9PmvQBIjrf2Oe4Nz3XHt7Ki2dauLijxN7iPTrxrfE4piNyMmBrbM71+Ls1b286zruoty927oLLex+34gDj5Fg4SpOhuwBvvPHGtNgxaXOSjJhB5xw4HokjUI9Rc6LtwN6KoCsq5xzRInV+RbUHfxmvycp4TRK+PGfhEh+WBugaWarDcQt4yHqH43EAn9mGiZDNOM6+jtfrL1om59EeyL/JGcZ4DM+kfJ8w0jrSQdfxjT/Cu4IHwZogpP8C45eMcUvAI4nsPN5EngAta/xiV9/4xjemd57cXfMuId8pCEWfevMFxlV04wGcgjCP//Cx3qvCN/TAcRy/4CsXsNmseuWVV6bHGn1lTxCPzuQ+6sKW/HsIbeGB8eOVRQL+APpkPiOvdO4qOd3FeKOXLuRLyNd7RuZcjyeiu+B7iSZ6DMd4Skt4ty2LX+X6dJeEjtLh9773vRO/8dwjt3i+BMZi3OzJImluP0t1blKWvOkD/+KR+P4+wCLYn0LjXfoQHdm0cbkTZEOBfJIDvHhwE7oeWp19sfPQJHaB9HKeDN2OkImUofcp2g9/+MPT/4W4xuAz9JwvQ+esXPOhAF9IO7aB53TQAOTKjt3vfatGvMdvY7bQMdEV6CzR51r1OOFDuEv197Lrc0DwZIOgRY6A85vf/OY0yV+/tevVoBdkLBXMKmMbXXMcDru5T7jKZtFJx+m6QMSjIv/+7/8+LSTUpdvGwCbwe0uw2LEbzbeBQxs5FjY+DoHO97znPdOdAn40ni/RlXyWrhlbPs0xfRJQtTPOlvVp3PAau3ILGnyzULMofPLJJ6fPpn/961+f8LWHrksGfLPQIQM6VICKL3ipHF+l/Od98ovMosmi1YKffMnZ43fexTQmwTa9XQLX3X1QV71A21sB/mmvNuV4a2FmYeO9KDasPL6TwxKgER55wK3tJdyblmmTXQO2DvTrsUb9Wuyg2xiy1/J0Q872bWyg0zk5AMfhTwVn/LOt9z1jRu1Duz8OMEgOx6Tu+X1/WOY/N7ykmaHKGbAcPifBsJ1n4MpNtDm6RrS1k9IeqJ/y+jvXPD6SVWOWx/+lcXed427SqO4S/l52ew7gMzsQlNiJ//nPfz5NlsqPDXSBfkjZbn2Se4kth9f1+8iz5Xnf+RkBGvAoiyBEuf/n8VgmfvI5xhzevJ2bnKNJssFjF1qwA+pvqU0Bk4BIIOmTxerazW58o80ZB5pdG8vn7dafMTq2uLGD73ErdfXJZydnORrgyvHJO3p8OVmr45pUnXmfl3Ju/PgqOaY/+Jk8lHV8CjwhO7RayHjywrGFtTuI7vKTNRkrXwM6Z6Fh0Qwve4K/1VhrJ93GR/3aABJX0F+bFfD4IGmNZvWAvOO1sd20HJ3Ahq/HTy1yJPSxrWhLH8JXp7EeOh7xp47O+Of4s9sZM28f2t1wQGDmsQfBGWfqC2cmS4HaGDRl8BwA58PYSzkjE6mynN0xRqCPnFB9RVvn0TX2r07XjS9QNsIxaR/7ue5xQZJ6aOSMm6DnY6htYzaRNya5dkb+wR0nvuru+S84QLfoi911ib0sQTIwabKd7373u1NQ7tl0sjLhHxPSbfIe5UvmATkXYDhGV7JXp3rKtgZ0aB9vBGz4uNYPXHxn6x7VwUt8fPrpp6fdaY+2APX5HnhbQXTyfYIzfSrD32S81JfdXWODSwb4DD/fNNaJz2vtaQOoC1dg6+tgFl4vvvji1K5xJ7v4oI42PS6knsAWoAuOa8qlfPaEcEE/87HjNT7LS+x9LF9jD55WRw7WZLrWxuOUazO5mqvpP3sQpJOjMbEnubEsAfroJFuR0svoXqpz3TJtjbyMF97Rob/4qgwe3oFD9MJRZ+RzbV6XtiV8ffPp+Wd3ZS0eu6O7RONS/41JH8YmKVsb2xItD71sOw/80Dmx03+yHOAgQY88cKLjDtCccM51bvCMG5SPdea447WbHHNAAhFOStsCfpO5INNjHnZXjUlCK5o4HQ5NrsyEISDIKaEjOpfGcBM6t65TQIc+Y8iROj9Ec0EXvsWXFrHqGXe82prmc2jP40jf+ta3pscU7NiTQzwbx6dMgv+DH/xg2okXmNp9pZMCYNe3gnlbztNvNCZb5QIGehDAk6oj96iJj4y4G5Cuhb9FXl/0UBBucYAnS4Bedi3IZ+fuZvjUvNyjOGwZsIOtIbtiE6Ntof8qiK/wRvzRvqL5kM3O+0mWxq3d2o5WbSqrTeXZumuj7J1Xb97PJZwbOx3EK3qGT8qcp48WDo+zOQFPyifgn7a3sp/kjj5y47cF4/3lgnkajmvgkFzhzVN6tKXc523iL7rxxHHzEF7TZ/xbAu0YV6l5bAn3NmXoctfU3TF3ZeOlNuf8nI9t7NfYXE+XHCe/Ee9cj/fFzrlK9ozGxflwPIze/9fIc0inOEy0Ac4P3Z7l966RP0i06EG/HS94cDgheTtE1fNC8V/8xV+c4hCvpGmctDjXNSeMP5x3kwy8cCvT2eigr+z8whAEPRY5Am8BuIk7npJDEG8F8nAF5uPCYZxEq7NljhbyTs+jLdk6J/POHSszJjRbkHnEpIB6S9pqS9944/0+i8Bo7Ho5XrJTtiygU48c5KcIeCmB0b6WxqcsXTn2WKJFn8n72H0+hPbjC5ukY3gz2rWXzW2IsXv2RBeXoK/dtfEGZ0s7j85kx1bRwn56HEyf6Rm8U7QRdJmPjQd/jKEU7XP+wlWPT+OTPHXimLy2BPwi+1H+W7Z/KW1tK5VL4do+zjvlACPnVDgUecHSlk57ywFx+GjkpNzN8eeaHP+XvvSlR5/97Gen4M11TpRDdZyD5HCVq+dO1kOCJgsyMoYxNSnOx4NHxk+2gExNzHbVPQrRxLhWf97eJZ6zDy8Be5bbzp9gHb/ifzxRJnlHBw7dc47fZLC1Pem/PtHgPFBOtnJgDCA7UO7YrqoAwheI6JfNjl58nyoc4QdfLFzsUK/xJNrR6f2c3lPAx1OE7AgPJTYqV95Ykk9yu4txRM/Yt7K7pOEuxnmdPow9ebEB52wgYK8eY2Ib3lvlO9f0zjVzyWjfjrO32rxpnv2qT6fSJXbTsWvGULppX8euF31y42oMh/o1RjLiM/A0/3WoznWuoQVfJeCcfexwfQ7si53r82yvcccc4HhGx/m4juiOyXyzO47J5ORRIQG7HR+7xCYmO+meDc6JcY4FHcpKHtnZakJ6k7A7OGjyS0YmjMa01D084zdxw3MXzBfzPO7nhVGTCMDTrSeSJXoeahnd8v6Gl73xDC+TheNAmR1hix02he9klM6Gd4xcH2zBY3TdBSF7/aPL9eSsHJ0Wvd6J8QjHCy+8MOmKzQR1toR4xG4d60OqfN6XcjRLaKGbjWOOeyrneIuvIJqNgx6MtMMDjXE6OdJP/I2PaKnvI3V58s3SQTZMDi1SnHtn1aLf+2HudErk1tdKlwamvnrmEnjmI7zeCtKR5CanYxZZ+nHdOJLzVv1u3Q66pWyEDIzjEN2NK1znUrzYgkY81GZ9aHPL9reg8aG0sS92HoqkLphOhp5TZfg50SbuU2ONgM5jBnbQBXXve9/7Jmdl4skZNgmgnfMyabmu3MQkCH1owb0xgFE+ZDcGUnNZmRSNX+rrYHYiTcpjsIlvOyxzgB1IeE2H6A1+kgOgUxJQRh4FP3TVnRLnW+vb2Gd0CNAsduRoQXd0ytVBB3nbwfb5Wouej3/849OGga+eAePbEvQdHdEtr2ze11iO1mx7LJ/Xue9ztJG9FH/xmA0eGusx6U5P6QE65OCU+XhMfmi7DR7H7BK4c8gWfI2Ub/zMZz4zfbLbY2x4tmYPfKl6LXi0lX5PDW/8Q7fqY+yn465v3O2tm2MPUjaiQXxl18lg3kljIa/Smhzmda9zjiZJ28do/zq0PGTcfbHzkKV3IbQLfjgcziXHzrmcquGbjNDpueUPfOAD0x0dz/WjX8p5FZRyssCYmhRckx4SRLvxCLztJBqD8a6Ba3hlcehTuBaH7nwps9jRzkPjw9pYj1XODugOG5GcjzyfH5MLwNcmeTmeHxvIFAjSChaiLztAF12y4PeImGOPlBkXfTBGgbG7U1tDtGgXPWs+xrXod6weGZyyrqJRImc6YMEpx8tDY92ax2N7ZIseNFh4R8uIc2nHZAHIio5ZsPzwhz+cAm/2YF7hI+kaGzkE+Esv8VjgDtjP1pAc9YN+OVAuAeM5VciHop0OerfWnO08vs1pV4635i3JvH8MGPUBL/nAHa7PgYcVTV1/fHuNM+EAZ2Qy5Fw4GZMAw+cIcqbyJvSODT8nywEXoIzXtbEW1NyEfb6ixvH5nKXHb/QlmZzQUt/RVZm+0IJGZeiVR1/1tqT1JuNbq2OSMPkKZE0WJmjnZLYGgl+PZvjKlgnDuydenMfD5Gy8JujGv9bWJZcXXKRL8hHG83DwtwWDMpMoHm8F2qwvOb2mG4I1ciZXdGeXzuk6fZHbjbaT7T2d2mJD6D7GoqKxR3O+4hA/0KKeRTqa46Gy6je+Q+1c59oo6/H4cdpAlzrsi93xqSDeOzb+MZ9OZj/aUUeebArCuqYKnuCDPDzlaIBfGz2+yvbJ33XXLhGMG2/oOD64q0NO/kASb/lZ1/EpXU1mc37he/KIn8lsjnvbc3KOdn1IINrmOjDvT11prFc7tTGvc93z+KUeevAY3e5w6kuZ92vxHO/5IPxeAvXYf3/2aWNT/fi8VOcmZWiOt2jis+U2Ktwll9COTrj1D0c9OfvKPtF4aE6+CY0Poc6+2HkIUrpwGjl6xswxZcycDCP3lTPG226V64w+Y3YtJyZwcq5uDgFr1dkS0Kl/jkbS59jfln2dUluN1cRhsSM5PgT4whGr+1u/9VvTnyR6/8TiZ4fjcIA9WISyA7bluEn/OD2+1aq+LF4kss82sw/n6ZFa8Nz1OzaMdESXMukQoJWt9zgY3VWHDxKMOOZfyg+19bjX0Cdpt7ajc82XwRfskLf3oIA6PoJCJo15pOFxaIaTj8ULOqVMqg/HtS/womvpnEWXd1A8qoh25UBblwr41fjx08aZhY4PkOCTTSE8PwVAB1ol8iNf0PxL39iBR7rZiHO6sATqWmTA11a6XL5U5yZltcce0CLZhLHIsXDBX5sX7qK5g7ZG76jjfJR2K7sJXUt18ET/aJXw2QIMP9GpjA3JyQIN8NGRbLQBx50qvGV/W9O5RPuple2LnVOTyE7P2zhg95+xcvyM2eMXdiXdOciZcq4M3nU5GJ2EY8/7mzDmoM6WUODYBLB1+1vSunVbxorXdmj9h0svwitbAvhvvPHG5HwFiIJFDnmH43HAxoDAg514X8fEh/cFKsfr+RcBtn5MxHQivZAraxKWw7sLmow3G9VvSVnlazzBQ6ng3cLdJkxfUhzHuNbGdcujie/jCwVqgL8hxyUQMPN/PmePJv8J5A9A+VD+Cp/VHwEf6mssd5zcOuab+Wj9OMaTfLK29QG0Cdi4APErX/nK9J8sPuBiHPDy8xPihf7Ed/yy4H/ve987bejhGf6Msgn3PlhV32wX0CG0SYJyH5tBr4UD2Wb3S7Tmk7Qx6uI41qV6Ny0babfIssHmkUG0+p+gD33oQ9Mfo+p/CaLL/CUeacN1CfemZfjAzvGNj7HY9eEj/bGrJ598crpTzu6jM9uM1/DMwxZI2htlFQ9uSt9Dqrcvdh6StC6U1iZPBsvwOReJoXocxu1jjsa1nCTDb7I18TJ4OK7PJ96tDV7fS2nrfk5RHTjSnKxFKpkdAnJJZurhW/I5VG+/dnMOmAzxnX0IOu1ouuvpQxp3AeygpL8m57GsY/ldATroIN60iFnrHx7+waWzdB0vfUURP/ka16TGsvU4BIfubFtctbhYszf0CuaM0cLCnYIWRmh0PTuMzrWxd12fjc2xxc6Xv/zlaXeez7Z40a5r+tA+/Hj17W9/ezp3R1dw+aMf/Wg61/4SPfV77jkeGb8cz+iZnJ4pl2cz982L6CBvtPHd9NKiweJa7u6ITSw4ZE8flkBdNkRXjPGYoP3mGXSxIV9K9el+/eM5/oPyOT3GoQ2yyXes4c7rXuccreix0OWnLXhsKuDlU0899ejpp5+e+IYGuKOuODYe47PY0Q6cY9B5nTHdB+6+2LkPru99XosDjJhhc0r/8A//MO2acp7eiTFJMnbBheuMmyE3uTJsTpgD1o5AJKdwLKPXd5OSPsAlOBdjbJzGPY698rng4ZAHwDepenPc/XwbDpik2ZO7Aq+++upkE3Y212S0Ta9vbyU5pwNL/Yfz9trblmSvghcBAX8ClmiqZ7oKl88RhMBFr7tlghE7scoOtVFb18mzEwubJ554Ytr1R4P++MAlsPBQz+fJLXYEdYJR45ZGMIaraJ7LhQ3jhTta7kToC33ajk/atMCKVp9Jt1lld5o/F8x5x7GAbKTpko7nvMVDNouf+ExH8RJfXct/3ieP0hcbjv7816LF4pd83/3ud09fU0S3hO4lMG7zs0X5iFPbS3VuUpa+j+3SOU99WJjZsNB//F3rA99HWdXuGv5NytHAF2kbXWyczetXGZ1AO1qip3HBUaYN9s/u1HFdUi6HcwmwL3YuQcoPfIwmSIbptrhdjU984hNTsObfoYHrDJ4xS+24ZPTKBAGMX1kOKiPnADremlXazenU79Z9nEp7xjp3nlfxlWzIFpChydBEucPxOJBO2kk3CdrRFJAI0o8N2aR+ssXRLtKX8MqPTVc84SfsRnsenm6OtI00RCd9tdCxCeN/oT7ykY9MdzYE/bWpDak6Yzs3OcYTbVmwWrx4XPQq0L/g02Ns3qVzrp3aMtaAPY7nlY+5+sbOd8JHiwWUuzSf/vSnp2tozDe3EaVMnxY2/Hc+XDv5Au1txauR5odyPOoKXpjP8EYuKav8vseUHhWQm597P4dPoSP8Ovl2d8f5EmjLBkx6Gc6W83P0ahsP9YV2euvOtusevUO3dEgP4SYTNIJD+I3nOjm5a1vsoy8LHYsy52zHXGkMaEXPUv+uwUlntKNdZUv416HvIeHui52HJK0LpZUz4kQZqGeX7Uwy9HYxlTNaxg6cLwHjDme8vrXBcypoNtHnEB2jtxcwXYenb84HbZyaicC5Z/+djw4MDlC+NsZxXHd9HH3yeIrWypfoMb5w8IPzVtcOIahuQdNSG5dehm9ePgV2RtONeDfnj2DEHR0TJnsyydNLslirM2/jcc7nbZGrPka9V4bedF3OBqrrHMATIKOZbmhja9CnwECfdqcPBTvGYVdV7g6JuxQep7VwzDdpB93abTxb0Bwfta9dNADlawDPYgcu3yMv4f9IXzTX7lKb9Vs9uI61nf6pV2CbTMc28Rdu/anfGOLdUt/nXhYPjBMf4q2X5uk9nuEnPGnk6Zw32dooE22O5/M61zlPB+XmLTpmA4VPsfi1EdBHMLRL5mvQONItbRpfOrZW7zrl+oi/9YNH6DI/u4430lX9uk4OyQIdyec6NF2Fq00LRYtHGyro5wNbtKgf7+TR3TE+OpbQmgy0E4+vouEcrq9r3jmMbh/D2XCAYbqF2x8gbuWsj8Egj7AI2jkpNHMynpn1YiG6lXFIOSsOR3nONmf2yiuvPPriF794DBKP0ib60W5cxm7cQQ648/J44DzHyxnjEZ4oA+qvtVFbl5rjdXcjPK6JfyY18lgCCxt4HjfyGWgTqTqjvJbqbVFGP/QlB+Vk63i0a+ddNxaLNIs6j8YY39agD7xECz+DL2s8oZctdvAR3V5sprenCMZhXOgsJXNjkeL9XdqZPpNxfBvlXtml5cmr4JR8LPSV4w+/SU7JjiyXoIUt3YYLkvMS/nXLagtNdN8Ch12wUXcQHwqgH6/ZP5DjGT6v8db1cJNL/Jgu7D8nxYFlCzkpEndiLp0DHA7guAUhnA/HzcGcIvQYFofpcRifs/QisT9G9JUykwHgLBtLjrZx2SHz/PBDAo6+gMrk4bjAqYl2Ph7jh4Nn+EGmJkl38kycpyrj+Tju8xwP6QrdEng7x/813tFLixw7xe5EeAQpOW05Dv2P7dIBiZzdqaMv4Sh3Lkc7m5eco9cjd87VFVQp3xoKeCxy8POZZ55Z7cK40IseC002zjeN412tfE8Xskn8zKemJ8qMB9zlGMhfSs7yyu6JTSfTbbwgD/Jyx8QcaKPC5plHGPlN19Zkxo96SoC9qQvg8xFbAXlpX7t8iX5s+D2kxQ79b/7BS/wprfkac7axw5drY7Sjrfi7t7MNB7bT+G3o2VvZObDIgRy/i5yq8zUHv9jAHRZyeIII/2fhGWSTjcDdble39wUWBXzGwrGOjtIOts/CPiQYHb9jUNnaOFyPDxaBJm+f1fSSqkeDCsBqb62dSy8X+PiUsEUMaAJe4ovFQotLOid4YlN09hiQnZKh/gRB7ILOd03/ZA1H7txja3Tjpz/96bTAef7556cPklhUrAUgN6Vfe1IBj4WgRc8aoBPt8OmtsSjbmq61/q9bHp/xH43RT+b4nZ1dt93b4s9pQSfapEsFuj/qE544zze6489+PLJa+SF+WRgJzOkqOIR7E56jL9/hmEw9ZvXQIL7I8YrvkVokzsdjnCXX7tOO5rTt52/nwL7YeTtP9pIT4wCHzolKHJHk+L4m6KvYwzl65EDQ7m6O3XbBkyBNLgFBp0mCw5QX8BmbR2Lsjj0kSEbJhnyMK3mtjQUfBIwmcF+ccRcML3Z4PA4UaNAjwSx7AeSwBPDwN71bw1uqe5syesAuJHdD0n3l6GE3jtGPNouw1157bbo76hOrvr5o4yDc29AyrxsP8U+gI+mn8jk+Ouk33jlGr3TKgD704q/gFxgn+sdxOod3F3qRj6gvOVpGek6Zp8egLT3Cg3RM0M03epeMr7Sx4UV1NhPPlmjx/hh5qx+Pk/0S/nXL0hW0Rkf9XLet+8ZHt4Q/5qTuUq3RlZ7OdXgNfy+/Xw7si5375f/e+2NwoN3IJmvnEkd7itDEYrHiYwo+p+o9CcFTdHOqjseJwbExcp7hnuL41mji/MnEGOxCehRvPsalugIuPMN1MQAAIABJREFUj1v47yQLQo9juavjxVb1gQm7iXWpjUsvS4/wXiKLNUjP5PgKV52t7an2os05ebIP8tZ30DU5/Q8Prg0Dj5SxJ3bRLrWAZCswfoBW/Igv0T7vp7EVjKpf3TnuqZynF8aHj+4M2GCwqGw8aMX7UTbHpB/P9OdOgDt+cueXDHhPVukkGfmgCP6QHXvw9TD/lSQgJ8s1cHeUbM0/6bLzjtfqPW55bSVH9oruUZ8et637xMNXCe100DjcEfPoYHJYo88GDH/20B47XxvPuZa/Nduc6wj3cT14DnBC7Z4YjMmAc82pyjsu+BgngHBNotriiHPS2huPt2CW/jwCYzJ6z3veM9HWp2zRFzSOzl3LsQrotBPt0e3c8SkC2tFmXB7h+5u/+ZuJ/rXHAIzBOAVdX/va16bA6w//8A+nR5U8ulR78Br/KY77vmnCG4n+jDq1FnDAtVAQCLEJC1P1soutxpP+Zl/o6zPX7tKgA050jrpO9nal0Wc3W1CnDK58a0ALoI+O9VPZUl/ZMVqiq/HwPXQeT6M1/KW2rluGtlHW+tUPXh3qx3WbCXKPyL788ssTfr4S/0H5Ibr0py+0SIFyCR9BeB3Hm3grmFTmc7/f+ta3psd9XUNjOLV9KXnypD9A0I3H7m7aGLKJFO9dd7wms3g4l9NWvKx97aEhnVfuPH2MPnJtXEs00Bc48gDt1a/spnm8jTYLG7aqPwsc596/w3O8dgda2RLQW8lcp647bVvSWp9owzMp/umH/+YjLbT0D9CcbqjnWB3jkRu/usmtvL7OOd8XO+cs3TMaW05TYMZRmUwd27Hy6VfnjNs1Bh8OA5c4JUG1OqOx3yWL0CflEHNGzoG843Dvkr7b9tXYTA52i8kB4H3jmvfB2XLWHs0QCHunSUC2w+NzAJ+beOk6W6H/azwnHzgmTziOTfiXNPEtcRfv0mHHwPkSCC4swIL4nd9RjrfH4Cna9J/co/GqviwsbLoI4Mjee17aUB796NYenUC/8iWoL7hwOq8+fUy/agdOeMrUFazx4WjyuC8/rm6LpaW+L6kMj/hGd3K899ndr1PjAblmD82x9JSv4VvSVWWOl4DOAXnHxk9XjgHpINrpG9psrHhf1pMF7tS4hv4lYDfqmOssQAF6o32pzk3KbEzpJ7vQB5vxOLAvVKIDDYH+G5tjdd19Ev+QRzYIH96ajdfeueT7YudcJHkh42C8jNPk6N0Ozt+EqTzHyNlyXpwEx+pcHY7BI2XwQA7BtbsweE5Gqq+cTv3Loy3chyRWwQ3gfHv0yESRzJbGoo6PERh3eJzyDo/PAXxLX9IltdOveUt4XcpO4JoULxWa9PEyPTzEw4JxuOpWh68ReOClBUnyqP0t+Mtm9Me/kaM+yU/5mgzho8t7Hx6LYp8+ZsF3stGRvjW9GWk3LnUk+HLBmPcR8aY28gnV7Rw9kney+AsbHAJMgf2lAxnGU/LtcWhPC+BxfD8lPqEZXQDt6ah5mh1YQKzpROOgl/BtftWOvHbDO0YujvDFxzZOP/jBDz567rnnJp1MZ+f9GrOkntiCDtPprYEOiGPYHPm78+RPjB33H0Z4DA+P43PnaLTI0YYy7QTjcWXnmu+LnXOV7BmNi7NjqBmyRzA8w8w5uhNg4jbxM37OBj6jNunKlcsZvYl9NHDH4/kx2ZZzRIuxjHk0oF0K95j0bN02PhsXxyuA8W/PfYxhra/kY8fZJEdmveO0Vmcv/2UOjJMbftKl7OCXMX9xJqBkT/SMrOz6+fM/f1h3qYBn+Q08DJQdgviI3wIKC/U+TMKG1U8+h9q57jULHH3Z4fUYjb7WgjJts8NvfOMb024wOX/oQx+a/GIffFB/XMA9Dj3GFt+MnT8W9KGNL+BrtZuf06Zzvhq+gM0YvvCFL0x/yOorY+pI9FJ+iUBf0jvHfGlfBqRvzYXjnNHxXfMrHSDjHq+jR3Th+9///vR4oo/t8O9kz05G+xrpNS4LcroD4sGIs8Vx+oi36KGv9Ja+WbB4XFA5epyv0aEdfG+Bb3zxYws6awM/2tjwuCdfbQFMJz7xiU88evrpp6d+9d3YHEvGiK4ey3P3zbny+9KZxnXX+b7YuWuO7/3diANN5O4CMHzG+uyzz06TtjwnqhzMnQ4nytAFBzkAdRg83LsA/Zb0W1I20uE4vLuga6s+kpFJA/3OjeUQwGuSIA+OvZ29Q/X2a29xoIlNCX7jY8dvYb11hN9kZDJnTyZ6O5pXyeqtFs73CA9KRrnGE3oLBHb8igVHAZ1rFpT8lPr5l7W2bsJN8hME2xjo/Sf2VqC41KYPf9AN7xY4tkNc4LlEGz3Jppfaq47xwdV3ASB8x8rhVZ6uKsOfF198caJfwDj3BUt9XkIZ3qQz2bLFIR65piy5xNf74ov+0cMO6CS6+RO2wCbomXdXX3rppTdp5neWwNjo5Pe+971Jl+hTC/Al/JuWxVv10U5HzTkeFZRsVui3u4yuL4G6aKa35KGO861B22iw0MET9p783dmJzkP94jl65elMtpgvO1T/HK7ti51zkOIFjIFBWrDYMbLzYmeDsTJcDoAhgwyY0xmPw8sZlV8A6+5siHZjOXwO1TG5JIM1h0ouTSYcuAmz8zsj/IF3FG/TcedN4ktDs5NJRnbV4ZGZ59Px/pIB3/gF+meX2l2Pgoo5X+g1vskFSn1EoQWFHWHtuZ4v2srnoI99oU1/Tz755CRHslS+BBYWXmimI+3uOkZjqXqVH6I3u5aDFl/0yP+JKU8H0Ymu+OEcLR5bcyzRR6Ce/i8d8CF+xWPnZJI+4VPn98UvNAXsobt79KA/OFZuLiBn4HwN6JFxNf41vNuUjzxjS+jyFIJNU3ZisYNeOstXKlsDtIYnPpEeZ/Gx1t68HH36YC9spP/rQxde69t19CaLcuXZIDz1R746xotLgX2xcymSfsDjZJAMlYGbID1Ly/g9f+4ahwByYoy8Y3lG3aTatVjifEuIntrUP2fkuWA7XnbpOKQcrbzzaHHb2fPLoLKxvXlZ1+4z51jRZSyOgbGP+XQy/MBtMiTTJkUydK1xxqOh6n74fxxgG/TFrqjJNr7hIYiHMcx7Gu7kmNQFyu9973un4F69rSH51259zGnKFrLd8KsPn/1bhJi4aye8LXJ9oUMfXv5FS3o8b9+1Foceq0WTIB8v8RV92tLmfKzztq57rm10sRuLqujQzqHArAAumtAVf+XpS2XX4XG02ITyoRF1JW3JtV17+sVjwbAFpbFYgI28jobr8uYc8PEqncEHCW+UsQHX6RZ5Pi6famdr/qRDfBAbMMfRBXdILHg8SYFecx49bVxLdBgTPGCuTl/QfqjeUluHytIzdNU2veU7zUEjT40F3hJEn/bgSYfsb6mNq8q0Tc7a5l9s9LJ5GyzpAjpcD+KVXHJdO9GpbG1MtXGO+b7YOUepntmYGCsDZeR2MjkmTlHZEszLx/PxeKnuFmV2dnImHAxa3drvWVvX0cGJuc7JG6M60cfp+gBDzhhdXRud8Rb0btUGusZJ2HgkY1ujWblJctxt7lhbEoDX+Lei91zawT8Lf4FGu4r0SsAQz8bcXQiLHY9A+DQ6mzJJZ2fH4gsayFNgRC/I1CStHK3OlTsGI83G6B0AyTsnJnqPcW0F6NIfGvTP1wjW9LMGeKYenuOhYARPa0c+jmGtneuW1372hWZAfmsQjutojteOO6czQLsATvRPBbOfxlfQrX9JO645rl/H0a2Zzh2rLynTt+NLhviGX3gpKcMXxxYNzrPZQ3KCz8YkdeL3GBzfhtf1rT30eY+EXb773e9+c2OCP9e3FP5Sn+EYNziEu1T/cctGPcSf9E15fY+0VDZvn66iES4Yj+e4tz0nc3zN5+gbXfV9VfuNoRy+urVzVf1zuL4vds5Bimc+hpweh8rYC+KUnyKMDsQOjB13wSi6jaEdrtFZKVdPAuGd4vjWaDJxGJO8yaJ8rQ4Zwi/ogiewBermnMvX2rnkcrpiA8AjDnL8pGsC9ZFvHVt8++ywHXh11CeHY9hTfSYf59FH5vSdnAPXALwSm2dD7kgV8M3brf5Nc/1Gi8WLhY4vMul7CegoO8Zju9e+NiXQU3aKMPI9u6Ij+ZxR9sljLDvWmOgeOvSpP3nnx+rzIbSbfpNPcqCj+GUjzBMC7JeuOsezJXDNXUp6mlzZkHa2BvQ1PwvM3b17KJB94LVjCb/k/NQS5Kvk8JKV4x1OjwPLFnJ6dO4UXTAHciLlHFLHp8gWwaTJxA62RY7HWoAXNX05pZdxXecojQe+SSjH6nlcL3g+JMjJy8d0aAzGjgcmRvywC+gPRd0JE3DWJrwdljkg0HG34wMf+MC0iCmQaTKOh9X+zne+M/FVPdfwvd3NcI6Rk6FEx+X67lwZepwD9i0Bj3OyBS/WezlXQHWMRUV8EuQIIvWTPU6EDD/1Dwef8W/r5/WH7jY5LNiNx8abDlQ2dhQ/xrKtj/WfnqaDyqJ16/4eSnvkQf/xJFtg1xYv5hTgnP65oxsP5+Mb8bOn/MMc9zbn6E2H5Gt2c5s+jlk3XW8c5fpc4y1+0lO4ychxbR2T3r3t63NgX+xcn2d7jTvmAGfDgXAkBUqczKlOiAIlixXP8vtakgnJIscnOL1zZDcd7SayHKnxOVfu2KNG2nlIgH60J6NoJ7dDYKKwADRp++KMYNyz/N5/SMba2CeSZS7in+DbQpGukQG+rfHd3R/XBULuUBT8xOvlXm5fik59krGc7utz1H06JNgFFg8et3v55ZcfvfDCC9Pz6q4b59rYbkNlAQv9tQAEazyJTrhw8FDKnm9DxzHq4hea0Zt+1A/6x3FmZ/CODWSM7/hWQmP8PXb/p9o+GUh4Qq/oo0c4+UZ3amxsKGcrHrlcA7yEh5/aA8eQq37IEein46ngAfygN9vAn5FH8W1pGOq5zn7Iaqy3hL+X3R8H9sXO/fF+7/kxOcCBNCGXn7JT4QAF7h4d8KiBP+8zQXGmHONIu2P48zLnh5zsY7LuTtEKUsnImIzfBJDMlogxTnwxGXunybn3HiwSLQzVB8q12flSW5daFk/iYwue+JEeleMlEAR1h0Jd/N0S6mds0yYA23AnL3rpB5CjkR7JBcICPLrw/PPPT/+n5b9YDunT2Nd1j/ERT6R4ujSGaK19gai7uejd8j2i2t8iNw58S+b466MW5DE+4qSvu7QzNKGN/eOh3Pka37fgxam3QTbJiy20CeTRNbLy8r+NIMlChx2t8cumApl71FK7xwQ0sJu71J+txpNt4JHElt1RtunGny4BvuIvG6K76j3EsS+N7RzL9sXOOUr1zMY0BmIcak5FforA8bmL8653vWtKgncTFeeI/iYmjlEKTGxN9srD6/pDyY3BBO0dC5PBITmZHOF41O+NN96YdvD94aF/pRZECorxr+DzofDgLulkHyDdasJNf+RkUI6v6Z08XTPhHxv8AbDFP9twh8adJf1KxoFOslYuiIAjV45uYxDwHQP0r48SvqzxZOQtuxYQuRPb4vEY9N22TeOT8E8g5z0o9oXX9wX5PJtB6PHeE/+xxvf7ovMu+81O9Ule9J9O4o0NIDYB8I7uydPHOZ3qwwHZ/Ja+tH6jmZ3qkwwfEuRf0M422ISvBVa+NhZ4FpLmO48Sb8nbtT738ptxYF/s3Ixve6075ICJzwJinAA5f4GFshxuJCkrgFPGYUlB+Mo67toWObok75wIgAQXnGD9lZukorWJCD0SfI7XcUFX9UY+bEHvVm2gF92S/3Dx+BFoTEv9mIi93O05dDv4diuN0w659tpV04byHd7OAfogFfzg1Rwqk8MlI4tMOaCv9GxLHqev5frVv91oduGcnOuTLjhWjh52Y0wCJ3SiT3JMN44B2tanPLqW+jGO+AWPfwrQLSDVDj+lrS0hHtUufgHlazTDQa9c8GzH2ntQNmXwvWvaSVcO0RwN6gG5wI+sHBt75dHpvLbzbewbHTaD5M8888xUV/vhTg1d2I/xp+M+csNevPNpcUp+7AOMcltikevhJIdj8FYf5IVmx/pyTt+kFlz0o+M5vfDUabOhRd2WeoA+46efcjpLB+XZgUdn3dnBc/nawg29rpnr5OauYwCa8ROdeIFOtNsgMHfaQMIzYzAudIHqydkXHxWPw9mSt8cY+5Zt7oudLbm5t3UUDjDMnBNHytHbSfGIi4DNxM0BCDIYb86dc+CElDN4L74LtJTB4zBy0ndh9PoY++m4HPPQBIw5h3QUph6h0fhuPHYgBS4mLOeNa94tuQq4yEeyQFybDOd19/O3OIC/+Ee3TYyHdMcEnk3BZ0/O12T0Vi/nf1SgZaR4QqeXgE5L8blAsqADX+mxcnzVTjhL7V23LHnzg4JfdFxlZ2hzB5X8vTfogw98JxtUN3gcPagvuGPfyvlbgdcS/+DjC36g49VXX53uWPATdsa9u4d3+ZJourQcH/OJgtlPfvKT05cWlbljjj9wpPsE9NBrPiS/kj9Bo7segvLvfve7U7BO18h3CbQFl55aaGQ76dhSneuWaVM/aAPpLp383ve+N71PaFHgS4wvvvji9Alt50uALu2wKQseOuxcm1uBPvATzfkmfbEbC98em2Vv+Zf6jxZ1LZgteMRLQLvgvvVnIuKOfvbFzh0xeu/m5hxgrBk9g/e4E+fJ2AXKJm4LG9cYPCOHn2Nt8mTo6oyGztg7vzmFj1cTXdFWv3Jlc6cT7uO1fBpYBU346SV4X86yuJyPbU4tufn6Gvlog7x3eHwOxF/5mNb02sTOJrILNuH9DcHKpQJeSXgjuMBH5wUOh/hCX+HJ8VEA4lE9NpBNFIgcaudxryVj9uLRr3zFoT7YoZfb4aOtO6gWS9E4718/a+Bafguf6BJ6LLyM2zk+pmPxEa5AVgApSHRHVzDvroUddUGbOofGskbTuZQ3frpINvTJHIcnzuO780Myukt+oDn/gS4L3tdff30Kys3R5ItuvsaCdgnoD73QFj3IDpdwtyijk5L5x8eE0MxO/NGyd209Noj2qwC96mrLGNP1q+o9znXy1T670TZ7YccWL3Tiwx/+8KNnn312uoZnUv3DJwv1bWqQjzGlQ/o/Ff15HF7cFmdf7NyWg3v9o3OAQTJghsvI3aHhGHuJ3QubnFTBCeOeA2ekrrYkuHdt6PVdv2PeMbpAuPNxnPJ5Y+BkAZnleNfobryuO5b2xc4at5bL8avUBBc/l2oIosiKbOwS2/EzifoIwKVC9pb+8SGSwGAJ4KXv+Mi/2MXGf38u+v73v38K6ka8pXZuWqZdfZG7YE1+yNZcU8f7b/4Alc/02JjyeT14VwGc6kUDHlhMCRDRNC52tBcv5XAtDAWVTzzxxESTD5Rok35qP/5eRcu5XTfPAfLFA7lFgA09vI738f8+eRWtcvImWz6FHli8Wth4P8/XSN35EIzTjSUwTkG5usbWuLbWg/gXj6PJotv/j7FjNF7VLxy6mq/QbvxYGt9Ny/BFYi90wGYBH6PvnpxwjGfsew3Qxu6kYy8k12i4z/JlT36fFO197xyYcYCDZ+x2DU2Idl48gmHHi+GXV20+8XNaEofAWXAK2juGY4qGpTw65teWnOoa7rzuKZ1z9qXr0F8dY1HvruVySjy8CS34taRDa22Z7OB7ZIRNtSNr4rx0oIsAf/iIpY0T1+G5zpfwNz4VL2h63/veNz3+YiMmP5N+O98C9KtNvs9dFItU9ErRP++nQIev7P+r4Odbx3rKHxcamyAXPe9+97unR4C0q898sZz/Deic4E19O9TGBMemlbbwXUB2iZAc8SAdw8vOk88os/viU/JFJ7l5ud+TF17u9yizhY7coofuoX3NDozPOG2+aFebjbV8i3Gms7WpT4sctotGizVjAWx61Nuxf/W0hVZgXLU54t32OHtAl40B9s532/DVP/rk+JW+6FMZepR1PXm5Hn+PQfNtx3yM+vti5xhc3dvclAOM0cTHOMFzzz03vbNjB8g1hlzicDghRi0HnKjrnALnFc508Q5v5doJKqHBeKI1WhoHOqWHBDlPYwPjhHXIoRqzuuE73+HxOUCn7Pya/Ny9NDnSK3q/BPjscRLvvNk08Hw6nl/6YgfPJHy0K927MEs85EvwF8/wUfDhcZJPfepT02ICj10nC7zNJpbaukkZe0KDoFKgBvRzyM4sRmz2COjyp9ncdWnI76ZjFikWLYJaj8i5bszxQD/xwDU8docejwG+o88iiN8zrksF9kxv4ge54h/ZKcdH5xI4JPNj85DcABrJ2mIHPe7YSRa0ZIpWOgenOnPamvPMBXCN9diAl/hsc0KOPnQYg4SONXA9m9OOc+NcG99aO49Trm2Pn3ockK3x32hNB7SBX/CCjuUl19Rxjs5wqnPO+fG16Zy5t4/tzjjAsBkmY+f0BXUZ+mjICOIsm1idN0EoZ+AcVE7qGAPQh/7rA30mdzvqbtMLTNGOHgGLyS164cITPHG62hivNb5jONTb8iKaRnrjg7EugfHihboCpXgmiFSHrOXagXcXE+ASnadchmcW/vjkmWwTNH6ymSWwc+qdN7xkT96t8nx9vF+qc92yZKbN2kVT546TOx2A37VR1sqMgz74M1K2okxgcgzQt8e8vMsiUFsD9AM2Sm+/+MUvTo+u9RhJ1+EY35Ywtym8A8oPAXnDbUGxVgfOSP9Sm2QAtEk+5CIn0xG0A3epPf3wddqA4xg0nrGdSzo2J+ABvUnfneMRfUvOj6NXcPBXCr98C56iqT7QaCHtEUmbKK7RCWXGBJb0IDr4er7L+OiR9tL1rWhGE1rkkvbZA/7oO5/kHERDNC7l2kCf9uAfGuNS/avKopmfye/Vz7wvuPGqYzkY60Tz44zvKvoeyvV9sfNQJHXBdDJexikxbsnxqQJ6LWii08LFJyK9kJvDMmmZCHKqLXpyUBzwD37wg1Md4kG6RudqjMluqZLrxm68eOZZZIGtnavewzIBaaN2l9q55DKBuQ884JmAAaRXS3yx4Laj/p73vGd6LEKAjscFm0t1rlu2ZJ9NwrU1nut/pFl918lcsMSGLOhM9h43KSipra1ydxTc6fL8/kjfvP3sVC5gQKOF5qE68zbu8jzbwVd8zjeNfI6eJdl1bet85Bc/IOBUVmC2dX8Ppb25vMgknXfN5hl/SZbmktF2xjFaLMGT1Afqj3wf8a97PLaFBvZJhnxKd+2u2+Z94OPT6P/wp7RGD37CkdNXx3T4LqA+9QvSF8foANmQa+P16eIF/uyLnQsU+kMcMgM2QXMm8gz6FMfS5CMItRvtPSMB5sc+9rFHH//4x6fn7DkiDssk5rjJzHg4Js/nCl4fEqC7caHb5CcdcrZk6bpcwOhYUGui9Py/9iQAZ4e3c0CATq8E6R5pyj7wcgl+8pOfTF9JstA0wdNTdSwyjwHZKn0H+k3364/+oxdu8g7fnSiLHc+ruxNlkXYMXdCf/vGhO4pX9RPN6qnvfC3wbKz3kSeDsW98xnfXRl1RBhrbWGfrY/yV9NVdDOfRsHV/D6W99ImtBBYR7NXHRLIRiwsLnyX5qmcTySOZ8NPl8bi2t8jRYH6m/2h9SID2bKEcn9j0mj3HTzlc6a4AvSV9LtnLSB/cS4d9sXPpGvAAxs+JNPFmtM6lU4SCOc/ye4GY47cb3acsPR/cONDPoeaYGg/n9RAnjMaBB/FhdMqNr9zYTdYWOvBb6PQohPbiVXl19/wXHDAZ0xf2gJ+O8W1t8h13hXt0RD383xKy2drUh40Ai387zWiEk4zRC0cuaLLg9Z8SFmef+MQnHn3hC1+YbAidS5N7/dw0RwdAk/Yfp49RJ6t/0/6PXc+40gm0Si0wxr4b01x+I85Wx/rHZ3oYffqPhq36eUjtkBGeyCV8AWzB3X72486Jj2Kw/fCXxsjWbZqRNTxgwcTfbgHJCY3ReQxfsgWth9pI59JBuGSwttBxnR/K95qr79L+041kWh7dcnJAkzzZKL9U2Bc7lyr5BzbunOmYn+oQOECBmrszvkTj+WWOs8DCGDhXDkr5OGEYk/N2yE51jEt0NS4OVsKHqyYAOBaExmwyB/5c0A5+L17jkbZNLviywy9zQPCCfyZcO734Bcp/GfvR9E6Kxyq9TKxuE/VVspq3c9V5+iAH6bRPHusbsAG0S+hlI47phUANHvtxV9RmAYDXRD4VbPAztqf/QPkSKEcjWoyvcazxfKmNuy5LHtGI13b+jWUc813SxabTDzRIzkd53CU9p9BX8wI5teHlzqb37NzV8Si0T5t71871dG+JdpsLr7322rTgSe61uYR/07JkqA9+pL5u2t591aN/aC8dooP9g8bu+K70Nl8aDehFx2jH+XPXxvJDYzrna/ti55yleyZjY6gZa45lLDu1YXIunJGA3ZfjBKAeJQAj3Y0p+sexaeOhgUmXg+WABVF2IAukD43H3Ry7914I91lNga1FYhO5uniT835ofLkrevFfAIv/h/iFzx5dw9d4apJWf0tIv7WNJovaF154Yep7DAoK1tBigWOXH21w/Iu5x8p8iciY0rGtac325BLao3uJJ+iDEx2dV3epzn2XJQ8BsMdqPWJr19+CA+8bizGkF8em2R0KOiuI906jz2JHx7H7PtX28Z7ukZd5hKy++tWvTot9j/a6K+PLdz7rzK7wK9nOx8TO1R/hGLJFQ7bjmE49REC7DRYbb2zaI7TGtQTZv/nLB5P6pPsS7tZl6JToSXl0ohsod9z1rWl4aO3ti52H
What is 424?
What is 3 hundreds, 12 tens, 4 ones OR 4 hundreds, 2 tens and 4 ones?
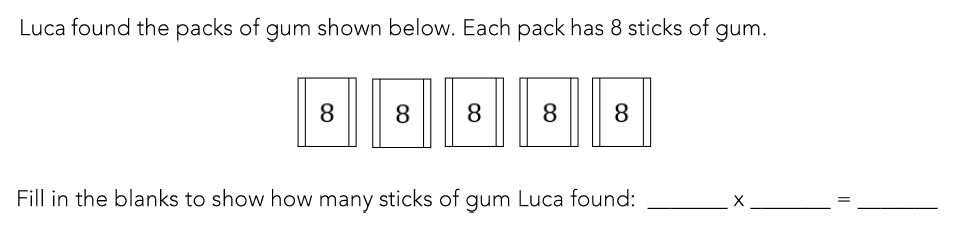
What is 5 x 8 = 40?
Identify the fraction that is greater.
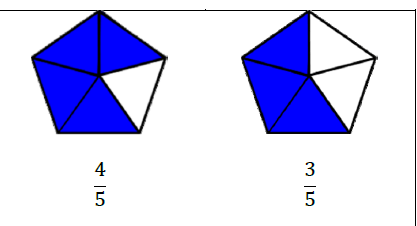
What is 4/5?
Part A
Jodieanne is making a pattern. Her rule is, "Start at 1,289 and subtract 100 each time to get the next number." Write the next three numbers in the pattern.
1,289, _____, _______, _____
Part B
Deondre made the pattern below. Fill in the missing numbers in his pattern.
3,359, 3,369, _______, ______, 3,399
What rule does his pattern follow?
What is 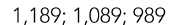 What is
What is 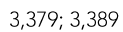
Mr. Walkes has 7 boxes of paintbrushes. There are 12 brushes in each box. How many paintbrushes does he have?
84 paintbrushes
a. 296
b. 309
c. 352
d. 288
What is 296?
Ms. Ekwunoh works at a bakery. She bakes 24 biscuits on a pan. She can fit 4 rows on a pan. Fill in the missing factor:
a. 4 x ___ = 24
b. Write a related division sentence to find the number of biscuits in each row. Use the letter B to represent the biscuits in each row.
What is 6?
What is 24/6 = B OR 24 / B = 6?
Orion, Cassiel, Luther and Samarrah share a cake. Show how to split the cake so that each person has an equal share.
 What would you call each share?
What would you call each share?
One whole is equal to ____ fourths.
What is one-fourth or a fourth?
What is 4 fourths?
___ = 75 + 892
Mrs. Robinson baked 17 peanut butter cookies, 16 oatmeal cookies, and 19 chocolate chip cookies for Ascend’s bake sale. She put 6 cookies in each bag. How many bags can she fill completely?
8 bags with 4 cookies left over
Ben rounds 514 to 510 when rounding to the nearest hundred. Is he correct?
YES or NO
Explain your answer using words, numbers or pictures
What is Yes?
Explanation varies
Create two expressions that are equal to 7 x 6
What is 6 x 7?
What is (7 x 3) + (7 x 3) OR (7 x 2) + (7 x 4)
Solve 700 - 77 = ____.
Round your answer to the nearest hundred.
What is 623?
What is 600?
Da Baby has 3 thousands, 1 hundred, 5 tens and 3 ones. Drake has 1 hundred, 3 ones, 3 thousands, and 5 tens. Whose number has a greater value?
What is they have the same value?
One hundred thirty-three people ordered lunch at the carnival. Forty-one people ordered hot dogs, 44 people ordered sandwiches, and the rest ordered pizza. How many people at the carnival ordered pizza?
What is 48 people?