Standard Form
Point Slope Form
Slope Intercept Form
Domaine and Range
Bonus
100
Daniel went to a fruit market where he found that oranges cost $4 per pound and bananas cost $2 per pound. He bought some oranges and bananas and the total cost was $28.
If "x" represents the pounds of oranges Daniel bought and "y" represents the pounds of bananas, write an equation that models this situation.
4x + 2y = 28
100
To lease a car, you must make a down payment when you sign the lease, and you must pay a certain amount per month. Osvaldo's lease says that he must pay $199 a month, and after 6 months of leasing his car, he has paid a total of $2,694.
Which is the proper Point-Slope Form equation to represent this situation?
y - 2,694 = 199(x - 6)
100
Elena borrowed some money from her brother. She pays him back by giving him the same amount every week. After 1 week, she owed $15. After 4 weeks, she owed $6. Write an equation in slope-intercept form that can be used to determine how much money she owes each week.
y = -3x + 18
100
For the function {(0,1), (1,-3), (2,-4), (-4,1)}, write the domain and range.
D: {-4, 0, 1, 2}
R:{-4, -3, 1}
100
A phone plan charges a monthly cost plus $0.30 per minute on data (not on Wi-Fi). In September, Maggie spent 120 minutes using data, and her bill was $51.
Identify the slope in this problem.
$0.30
200
James has $28 to spend on comic books and action figures. Comic books cost $7 each and action figures cost $4 each.
Let x = # of comic books James buys
Let y = # of action figures James buys
What equation should Priya use to help James calculate his spending?
7x+4y=28
200
To perform car maintenance, a mechanic charges for parts and $40 an hour for labor. The total cost that Terri spent for 3 hours of car maintenance was $200.
1. Write the linear function into point slope form.
Rearrange the equation to solve for y.
y − 200 = 40( x − 3)
y= 40x + 80
200
Shirelle is saving up to buy a pair of sneakers. She has already saved $20.00 and will receive $10.00 a week for doing household tasks.
Write a linear equation to represent this scenario.
y=10x+20
200
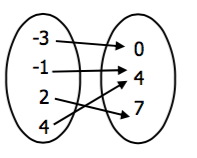
{0, 4, 7}; Yes.
200
An international phone plan charges a flat rate plus a fee per minute, regardless of the country the call goes to. A 10-minute call to France costs $3.19, while a 15-minute call to Spain costs $4.29.
Identify the two points given in this problem.
1. (10, 3.19)
2. (15, 4.29)
300
Andre’s coin jar contains 80 cents. There are no quarters or pennies in the jar, so the jar has all nickels, all dimes, or some of each.
The equation 5n + 10d = 80 represents the number of nickels, n, the number of dimes, d, and the amount of money, in cents, in the coin jar.
What is the number of nickels in the jar if there are no dimes?
What is the number of dimes in the jar if there are no nickels?
n= 16
d= 8
300
Using point-slope form, write the equation of a line that goes through the point (3, -5) and has a slope of 2. Then, rewrite the equation in slope-intercept form.
Point-Slope = y + 5 = 2(x - 3)
Slope-Intercept = y = 2x - 11
300
A hot air balloon is at an altitude of 500 feet. It begins to descend and after 2 minutes is at an altitude of 300 ft. The graph represents the change in feet, y, over time, x, minutes.
Write an equation in slope-intercept form that represents the function.
Explain the meaning of the equation in terms of the situation.
y = -100x + 500
This means that the hot air balloon began at an altitude of 500 ft and is descending at a rate of 100 ft per minute.
300
-3 < x ≤ 5
300
Identify the slope and y-intercept of the linear functions.
1. 3x + 5y = -15
4x − 3y = 6
Slope = -⅗; y-intercept = (0, -3)
Slope = 4/3; y-intercept = (0, -2)
400
Find the x and y intercept.
Equation A: 4x + 5y = - 20
x=-5
(-5, 0)
y=-4
(0, -4)
400
Tyler teaches painting classes in which the amount of money he makes depends on the number of participants he has. For each additional participant, he earns $35. For five participants, he earns $225.
Using point-slope form, write the equation of the line that describes this scenario. Then, rewrite the equation in slope-intercept form. What does the y-intercept represent in context?
Point: (5, 225)
point-slope form: y - 225 = 35(x - 5)
slope-intercept form: y = 35x + 50.
In this problem, the y-intercept of 50 tells us that when there are 0 participants, Tyler earns $50.
400
Maci’s aquarium has a leak. The aquarium holds 75 gallons of water when full and is leaking at a rate of 5 gallons per day.
Write a linear equation to represent this scenario.
How much water will be in the aquarium after 4 days?
y=-5x + 75
After 4 Days there will be 55 gallons left in the tank.
400
The set of ordered pairs shown represents a function, f.
{(-6, 3), (-2, 9), (3, -2), (0, 6)}
Select the THREE ordered pairs that could be added to the set so that f remains a function.
(-3, -4)
(-2, 0)
(0, -1)
(1, 6)
(2, 3)
(-6, 9)
A, D, E
400
A mountain road is 5 miles long and gains elevation at a constant rate. After 2 miles, the elevation is 5500 feet above sea level. After 4 miles, the elevation is 6200 feet above sea level.
Find the elevation of the road at the point where the road begins.
Describe where you would see the point in part (1) on a graph where y represents the elevation in feet and x represents the distance along the road in miles.
The beginning elevation is 4,800 ft
The point would be at (0, 4800), which would represent 0 miles down the road, or the beginning of the road, being at an elevation of 4,800 ft above sea level.
500
Equation 2: 2x + 4y = 40
What’s the number of rides the student could get on if they don’t play any games?
What’s the number of games the student could play if they don’t get on any rides?
10 (mark the point (0, 10) on the coordinate plane and ask students what this point represents). Make sure students are able to use the vocabulary “y-intercept” as well as being able to explain what this point represents in context.
20 (mark the point (20, 0) on the coordinate plane and ask students what this point represents). Make sure students are able to use the vocabulary “x-intercept” as well as being able to explain what this point represents in context.
500
In addition to a flat hourly rate, Elena’s aunt pays her $1.50 for each call she makes to let people know about her aunt’s new business. After 10 phone calls, Elena earned $25.00.
Using point-slope form, write the equation of the line that describes this scenario. Then, rewrite the equation in slope-intercept form. What does the y-intercept represent in context?
Point-Slope: y - 25 = 1.50(x - 10)
Slope-Intercept: y = 1.5x + 10
In this context, the y-intercept of 10 tells us that Elena earns a flat rate of $10 before making any phone calls.
500
Lin’s dad bought a tablet. He pays the same amount each month for a subscription to a movie streaming service. The table represents how much money he spent, y , for the tablet and streaming service for x months of the service.
Write an equation in slope-intercept form that represents the function.
Explain the meaning of the equation in terms of the situation.
y = 15x + 750
This means that the initial cost of the tables was $750, and Lin pays $15 per month for the streaming service.
500
y=distance from home in meters
x=time in seconds
What is the range of this function? What does it represent in context?
What is the domain of this function? What does it represent?
Range: 0 meters to 160 meters; {y | 0 ≤ y ≤ 160}; Represents distance from home to the bus stop
Domain: 0 seconds to 120 seconds; {x | 0 ≤ x ≤ 120}; Represents the amount of time before getting on the bus
500
y = 5,520.619x - 1,091.393
What is the slope of the line in the scatter plot?
What does the slope mean in context?
Is it a positive or negative correlation?
The slope is approximately 5,521.
If the weight of a diamond increases by 1 carat, the model predicts that its price increases by about $5,521.
As weight increases, price tends to increase. (Positive Correlation)