Know Your Formula
Plug it In
Surface Area Practice
Volume Practice
Name That Shape
100
What is the formula for the surface area of a rectangular prism?
SA = 2l × 2w × 2h
100
V = l × w × h.
Find the volume if l = 4, w = 3, h = 5.
60 units³
100
A cube has sides of 5 cm. Find the surface area.
150 cm²
100
Volume of a cube with side 4 cm?
64 cm³
100
A 3D shape with two triangular bases and three rectangular sides.
Triangular Prism
200
What is the formula for the surface area of a cube?
SA = 6 × s²
200
SA = 6 × s².
Find the surface area if s = 7.
294 units²
200
A rectangular prism: l = 3, w = 4, h = 2.
Find SA.
52 cm²
200
Volume of a cylinder with radius 2 cm and height 10 cm?
V = π × 4 × 10 = 40π ≈ 125.7 cm³
200
A shape with six matching faces.
Cube
300
What is the volume formula for a triangular prism?
V = (b × h ÷ 2) × l
300
V = (b × h ÷ 2) × l.
Find the volume if b = 6, h = 4, l = 10.
120 units³
300
A triangular prism has bases with area = 12 cm² and perimeter = 18 cm, height = 5 cm.
Find SA.
SA = 2×12 + 18×5
SA = 24 + 90
SA = 114 cm²
300
Volume of triangular prism with base area 20 cm² and length 6 cm?
120 cm³
300
A prism with circular bases.
Cylinder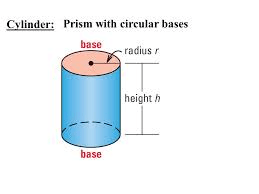
400
What is the formula for surface area of a triangular prism?
SA = Base Area × 2 + Perimeter of Base × Height
400
A rectangular prism: l = 8, w = 3, h = 2.
Find its surface area.
SA = 2(8×3 + 8×2 + 3×2)
SA = 2(24 + 16 + 6)
SA = 92 units²
400
A cube’s surface area is 216 cm².
What is the side length?
216 ÷ 6 = 36 → √36 = 6 cm
400
A rectangular prism has volume 240 cm³ and base area 30 cm².
What is its height?
8 cm
400
This shape has a single base and comes to a point.
Pyramid or Cone (context-dependent)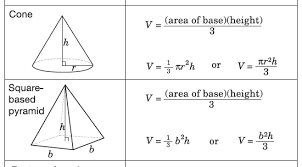
500
What is the formula for the volume of a cylinder?
V = π × r² × h
500
A triangular prism has a triangle base of b = 5, h = 6, and prism height of 10.
Find its volume.
Base area = 15, Volume = 15
15 × 10 = 150 units³
V = 150 units³
500
A cylinder has radius 3 cm and height 7 cm. Find the surface area. (Round to nearest cm²)
SA = 2πr² + 2πrh
SA = 2π(9) + 2π(21)
SA = ~56.5 + 131.9
SA = 188.4 cm²
500
A triangular prism has base triangle with b = 10 cm, h = 4 cm and prism length 12 cm.
Find the volume.
(10×4 ÷ 2) × 12 = 20 × 12 = 240 cm³
500
A prism with no faces or base
Sphere