Clustering?
Outliers
Positive or Negative?
Linear or Nonlinear?
100
Is there a cluster in this scatter plot? If there is, point to it.
Yes, there is a cluster.
100
How many outliers are there in this scatter plot?
There is one outlier.
100
Is there a positive or negative correlation?
There is a positive correlation.
100
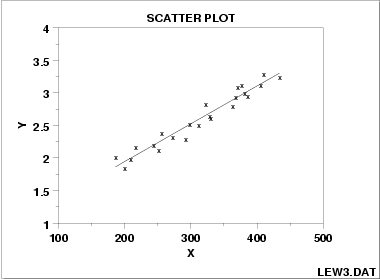
Is there a linear or nonlinear correlation?
There is a linear correlation.
200
How many clusters are in this scatter plot?
There are 2 clusters.
200
What is the point of the outlier in this scatter plot?
The point of the outlier in this scatter plot is (2, 16).
200
Describe this correlation.
A strong positive correlation.
200
True or false: This is a nonlinear correlation.
True.
300
Which cluster is bigger?
The green one.
300
Explain why there's an outlier in this scatter plot.
There's an outlier in this scatter plot because one of the data points is placed far from the rest of the data points.
300
Why is this a positive correlation?
This is a positive correlation because as x is increasing, y is increasing.
300
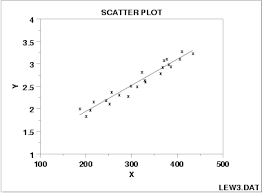
Describe this relationship.
A strong linear relationship.
400
Explain why there are clusters in this scatter plot.
There are clusters in this scatter plot because a group of data points are close together.
400
Which of these points is not an outlier: (140, 40) (175, 40) (145, 80) or (175, 69)?
(140, 40) and (175, 69)
400
Explain why this is a negative correlation.
This is a negative correlation because as x is increasing, y is decreasing.
400
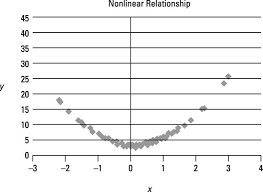
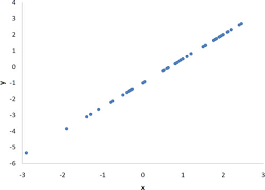
Which of these scatter plots is linear?
The second scatter plot.
500
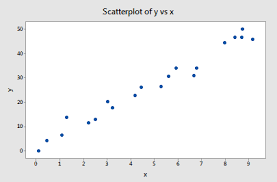
Why isn't there a cluster here?
Because the data points are spread out.
500
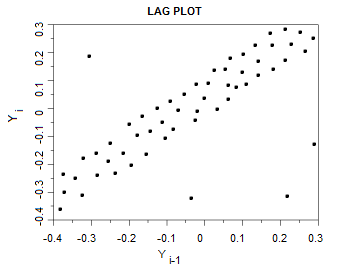
What are the outliers in this scatter plot?
Point (-0.3, 0.18), point (-0.04, -0.34), point (0.22, -0.34), and point (0.29, -0.13)
500
Why is this a strong negative correlation?
This is a strong negative correlation because the data points are close together and as one variable is increasing, the other is decreasing.
500
Explain why this is a nonlinear correlation.
This is a nonlinear correlation because the line is curved.