Segment Addition
Angle Addition
Angle Relationships
Proofs
Double Point Problems
100
Given two points A and C, a third point B lies on the line segment AC, then AB + BC = AC.
What is the definition of Segment Addition Postulate?
100
The postulate describes that putting two angles side by side with their vertices together creates a new angle whose measure equals the sum of the measures of the two original angles.
What is the definition of the Angle Addition Postulate?
100
A, B, and C are collinear. What is the relationship? Find "x".
Supplementary Angles
X = 25
100
Which step is missing here?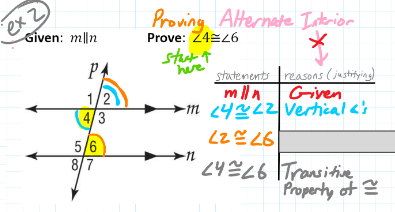
Corresponding Angles
100
I asked you all what you did this past weekend, but what did I do?
Multiple possible answers
200
What is R?
R is the midpoint of the line segment TY.
200
State the angle addition postulate with the following angle.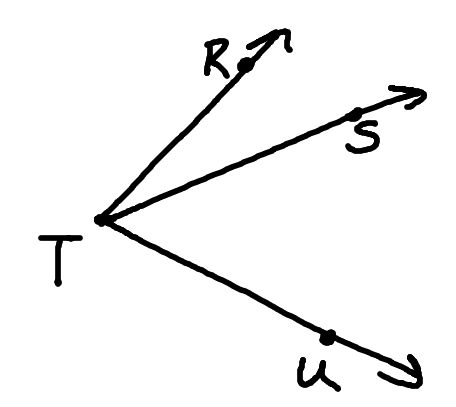
angleRTU~=angleRTS+angleSTU
200
Name all Corresponding Angles:
\angle 1 \cong \angle 3, \angle2 \cong \angle 4
\angle 5 \cong \angle 7, \angle 6 \cong \angle 8
200
What is the hidden phrase in this picture?
Skating on Thin I's (ice)
200
Points G, H, I, and J are collinear IN THAT ORDER.
GH = x +17, HI = x +19, IJ = 8 and GJ = x +34
Find GH.
What is 7?
300
Y is the midpoint of segment TL. Find x and find TL.
x=9
TL=110
300
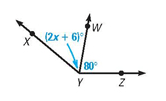
Find "X" if m\angleXYZ = 160
What is X = 37?
300
If the measure of angle 4 is 112, what is the measure of angle 6?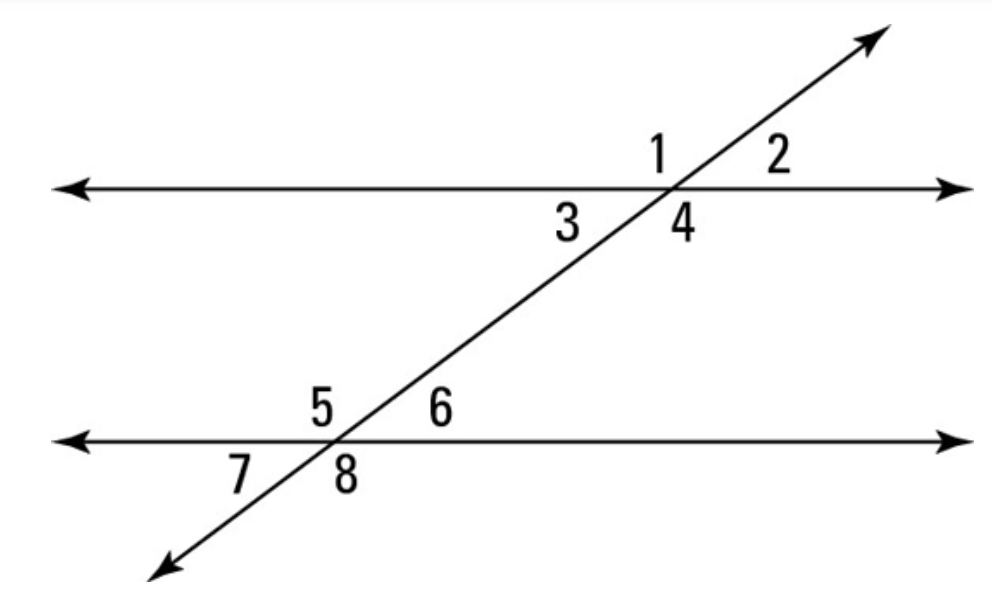
m\angle 6 = 68^\circ
300
Find BC using a proof setup.
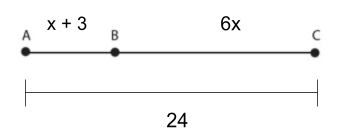
\overline{AB} + \overline{BC} = \overline{AC}, \text{segment addition}
x + 3 + 6x = 24, \text{substitution}
7x + 3 = 24, \text{simplify}
7x = 21, \text{subtraction property}
x = 3, \text{division property},
\overline{BC} = 18
300
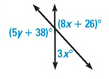
Angles side by side add to be 180. Find "x" and "Y".
What is "X" = 14 and "Y" = 20?
400
Point B is somewhere between A and C.
AC = 3x + 3,
AB = -1 + 2x,
and BC = 11.
Find "x"
What is x = 7?
400
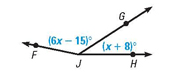
Find "X" if m\angle FJH = 147
X = 22
400
If m\angle 2 = 4x + 42 , and m\angle 7 = 3x + 45 , how much is m\angle 7 ?
X = 3
m\angle7 = 54
400
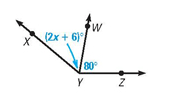
In the diagram, the measure of <XYZ is 140 degrees.
Find the value of X using a two-column proof.
m\angle XYW + m\angle WYZ = m\angle XYZ, \text{Angle Addition Postulate}
2x + 6 + 80 = 140, \text{substitution property}
2x + 86 = 140, \text{simplify}
2x = 54, \text{subtraction property}
x = 27, \text{division property}
400
The measure of angle G is six more than twice the measure of angle H. If angle G and angle H add to be 90, find the measure of angle G.
What is 62 degrees?
500
B is the midpoint of line AC.
AB = x + 6 and
AC = 3x - 31.
Find "x"
x = 43
500
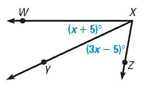
Find "X" if the ray XY was an angle bisector.
X = 5
500
If m\angle 1 = 5x + 3 and
m\angle 7 = 8x -5
then find m\angle 1 .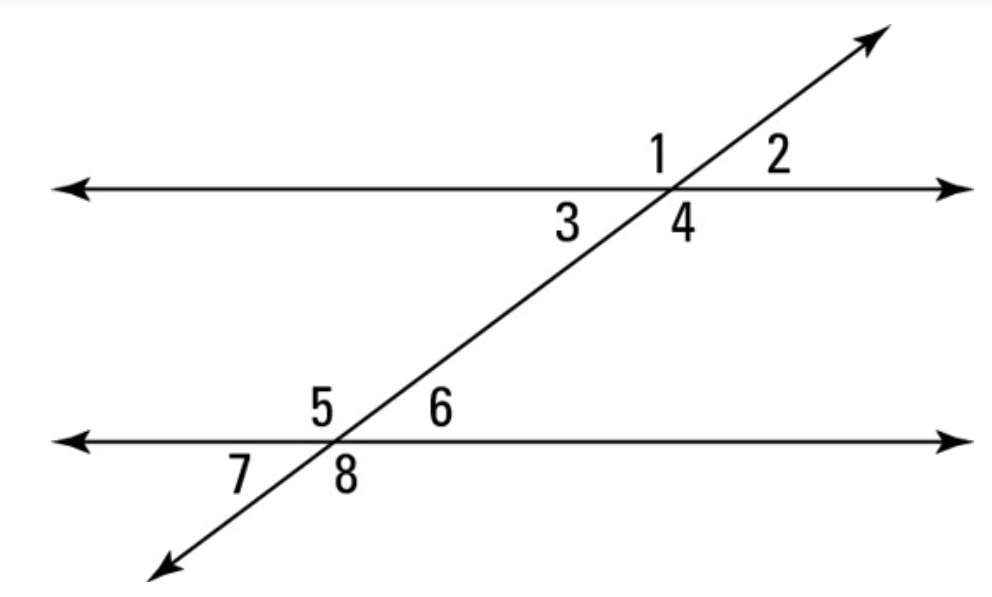
x = 14.
m\angle 1 = 73^\circ
500
Given: x||y
Prove: m\angle 9 \cong m\angle 15
x||y, \text{given}
m\angle 9 \cong m\angle 11, \text{Vertical Angles}
m\angle 11 \cong m\angle 15, \text{Corresponding Angles}
m\angle 9 \cong m\angle 15, \text{Transitive Property}
500
Given: a||b, x||y
Prove: m\angle 12 \cong m\angle 6
There are multiple different ways to prove this.
m\angle 12 \cong m\angle 16
m\angle 16 \cong m\angle 6
m\angle 12 \cong m\angle 6