Polynomial Operations & Compositions
Review: Quadratics
Graphs of Polynomial Functions
Factoring, Zeroes, & Multiplicity
Laws of Exponents & Simplifying Radicals
100
Use the following functions to answer the question.
What (f - g)(x)? Then find (f - g)(1).
f(x) = x^2 + 5x + 1
g(x) = 3x - 7
(f -g)(x) = (x2 + 5x + 1) - (3x - 7)
= x2 + 2x + 8
(f - g)(1) = 11
100
Identify the vertex:
y=5(x-8)^2+2
(8, 2)
100
Identify the Relative Minimum and Relative Maximum.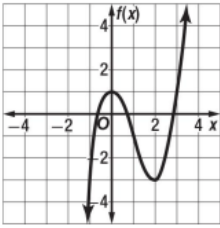
Rel. Min. = (2, -3)
Rel. Max. = (0, 1)
100
Factor to find the zeroes.
y = h2 + 12h - 28
(h + 14)(h - 2)
h = -14, 2
100
Simplify:
\frac{21d^{18}e^3}{7d^{11}e^5}
\frac{3d^{7}}{e^2}
200
Use the following functions to answer the question.
What (g * h)(x)? Then find (f * g)(-1).
g(x) = 5x + 1
h(x) = 3x - 7
(5x + 1)(3x - 7) = 15x2 - 32x - 7
(f * g)(-1) = 40
200
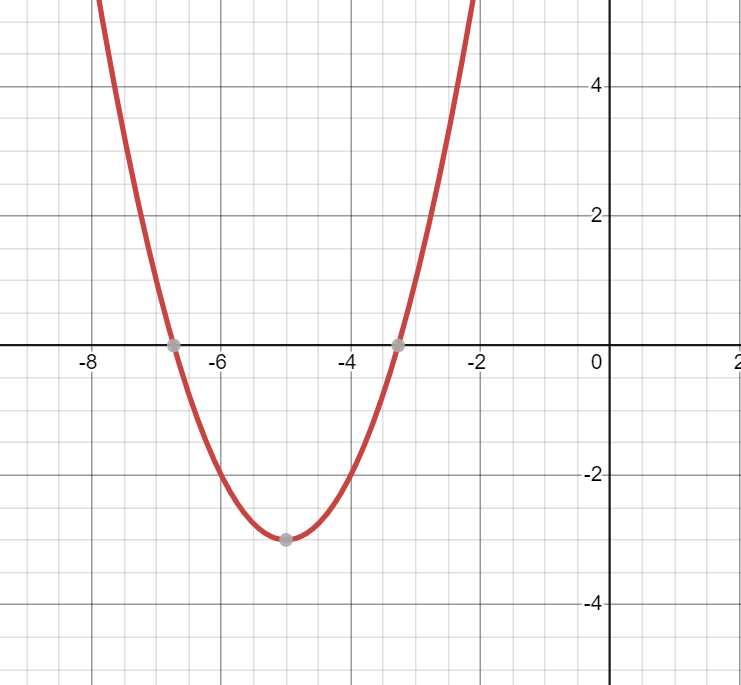
Identify the vertex, axis of symmetry, maximum/minimum, and if the parabola is concave up or down.
Vertex: (-5, -3)
AOS: x = -5
Minimum at y = -3
Concave Up
200
Determine whether the degree of the polynomial is even or odd, and if the leading coefficient is positive or negative.
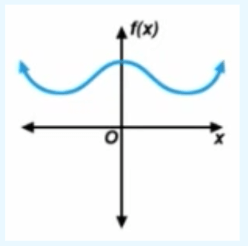
Even, Positive
200
Identify the zeroes, the multiplicity at each zero, and the effect it has on the graph.
The amount of crosses at the zeros for the equation
y = -7x (x+4)5 (x-1)8
x = 0, Mult. 1, Cross
x = -4, Mult. 5, Cross
x = 1, Mult. 8, Bounce
200
Simplify:
\sqrt{64m^3n^3}
8mn\sqrt{mn}
300
Use the following functions to answer the question.
What is f(g(2))?
f(x) = x^2 + 1
g(x) = 3x - 7
h(x) = (x-2)/3
f(g(2))= 2
300
Find the axis of symmetry and vertex of the quadratic.
f(x) = 3x2 - 12x + 7
AOS: x = 2
Vertex: (2, -5)
300
State the end behavior of the polynomial: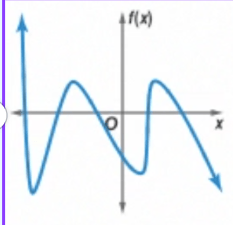 
As x approaches negative infinity, f(x) approaches positive infinity, and as x approaches positive infinity, f(x) approaches negative infinity.
300
Factor, identify the zeroes, and the multiplicity at each zero.
a(x) = 3x3 + 6x2 + 3x
3x(x2 + 2x + 1) = 3x(x + 1)2
x = 0 (mult. 1), -1 (mult. 2)
300
simplify:
root(3)(-250p3q7)
-5pq2root(3)(2q)
400
Divide the following polynomials using long or synthetic division:
(p^3 - 10p^2 + 20p + 26)/(p - 5)
p^2 -5p -5 + 1/(p-5)
400
Solve the following quadratic equation by factoring: 5x2 + 8x - 4 =0
x = 2/5, x = -2
400
State the domain and range of the polynomial:
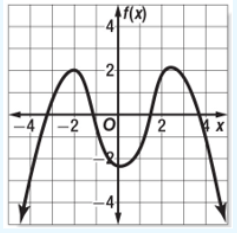
Domain: R
Range: y < 2
400
Factor and identify the zeroes.
f(x) = (a2 - 4a + 4)(a2 - 25)
a = -2, 5, -5
400
Simplify:
4a3b2 (3a-4b-3)
\frac{12}{ab}
500
Use the following functions to answer the question.
What is g(h(x))?
f(x) = x^2 + 1
g(x) = 3x - 7
h(x) = (x-2)/3
g(h(x)) = x - 9
500
Solve the following quadratic equation using the quadratic formula:
3x2 + 23x + 14 = 0
x = -2/3, -7
500
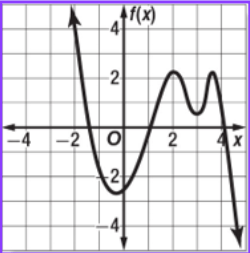
State the increasing and decreasing intervals of the polynomial:
Increasing: (-.5, 2), (3, 3.5)
Decreasing: (-inf, -.5), (2, 3), (3.5, +inf)
500
Factor and identify all the zeroes.
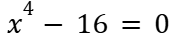
(x2 + 4)(x + 2)(x - 2)
x = 2i, -2i, -2, 2
500
(\frac{36a^5}{4a^4b^5})^{-2}
\frac{b^{10}}{81a^2}