Arithmetic and Geometric Sequences
Sums of an Arithmetic Sequence
Slope-Intercept Form
Point-Slope Form
Standard Form
100
This type of formula is used to find the term in a sequence based on the previous term in the sequence and the common difference/ratio.
Recursive Formula
100
The sum \Sigma_(i=1)^(5) 2i+1 is written in ________________ notation.
Sigma or Summation Notation
100
What is the general equation for a line in slope-intercept form?
y=mx+b
100
What is the general equation for a line in point-slope form?
y - y_1 = m(x - x_1) OR y = y_1 + m(x - x_1)
100
What is the general equation for a line in standard form?
Ax + By = C
200
Is the following sequence arithmetic, geometric, or neither?
15, 10, 6, 3, 1, 0, ...
Neither
200
What is the formula for finding the sum of any finite arithmetic series with n terms?
S_n = (n(a_1 + a_n))/2
200
What is the slope of the line that passes through the points (1, 7) and (10, 1)? Write your answer as a simplified fraction.
-2/3
200
Write the equation of a line in point-slope form that passes through the point (2, 1) and has a slope of m=2.
y-1=2(x-2) OR y=1+2(x-2)
200
Find the x-intercept of the equation 2x+3y=12
x=6 or (6, 0)
300
What is the explicit formula for the nth term of an arithmetic sequence a_n given the first term of the sequence a_1 and the common difference d ?
a_n = a_1 + d(n-1)
300
Can we use the formula S_n = (n(a_1+a_n))/2 to find the sum of the sequence 3, 6, 12, 24, 48? If so, find the sum. If not, explain why not.
No, the formula S_n = (n(a_1 + a_n))/2 can only be used to find the sum of a finite arithmetic sequence. 3, 6, 12, 24, 48 is a geometric sequence.
300
The amount of water in a tub can be modeled by the equation y=-2x+20 . For this problem, y represents the amount of water in the tub (in gallons) and x represents the amount of time that has passed (in minutes). Interpret the slope in the context of this problem.
The amount of water in the tub is decreasing at a rate of 2 gallons per minute.
300
Write an equation in point-slope form for the line shown below.
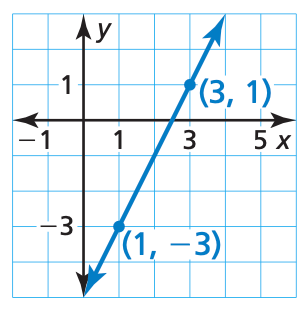
y + 3 = 2(x-1) OR y - 1 = 2(x-3)
300
A hockey team coach tells his players, "We need 20 points to make it to the playoffs. We get 2 points for a win and 1 point for a tie." Write an equation in standard form that represents the possible values of W wins and T ties that will let the team make the playoffs.
2W + 1L=20
400
Write the recursive definition for the following sequence:
11, 14, 17, 20, 23, 26, 29, ...
a_1 = 11
a_n = a_(n-1) + 3
400
Find the following sum:
\Sigma_(i=1)^(4) 3i-1
26
400
The table below shows the height of an elevator above ground level after a certain amount of time. Write an equation in slope-intercept form that gives the height, y, in feet after x seconds have passed.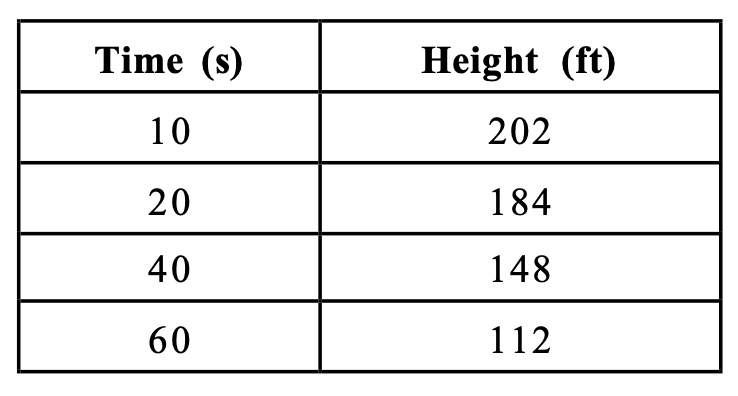
y = -1.8x+220
400
Write an equation in slope-intercept form that goes through the points (7, 2) and (2, 12). Hint: think about writing the equation in point-slope form first, then converting to slope-intercept form.
y=-2x+16
400
You are helping to plan an awards banquet for your school, and you need to rent tables to seat 180 people. Small tables seat 4 people and large tables seat 6 people.
Let x = the number of small tables and y = the number of large tables. Calculate AND interpret the y-intercept.
The y-intercept is 30 or (0, 30). This means that you will need to rent 30 large tables to seat 180 people if you ONLY used the large tables.
500
Find the 26th term of the sequence with a_1 = 23 and d=4
123
500
Find the following sum:
\Sigma_(i=1)^(20) 2i + 3
480
500
Giselle pays $240 in advance on her account at the athletic club. Each time she visits the club, $15 is deducted from the account. After how many visits will she have $0 left on her account?
16 visits
500
You are designing a sticker to advertise your band. A company charges $225 for the first 1,000 stickers and $80 for each additional 1,000 stickers. What is the total cost of 9,000 stickers?
$865
500
At a recent basketball game, adult tickets were sold for $4 and student tickets were sold for $2. The total revenue was $692. How many students attended the game if 78 adults attended the game?
190