Terminology
Venn
Lucky Dip
Random
100
What is a Universal Set?
In set theory, it is generally the largest set or all of the things you are interested in examining.
100
What is a Venn Diagram?
Is a diagram that is used to represent sets. Usually made up of 2 circles and a box
100
Set notation:
U means?
UNION = ELEMENTS IN BOTH SETS. = AND
100
Set theory utilizes Venn diagrams because they are pretty
False,
Set theory utilizes Venn diagrams because it is a very clear way to show the information
200
What is a set?
A set is a collection of things or objects that have at least one variable in common.
200
Why is it a visual representation?
Because it shows the universal set as a rectangle and how the sets are related between each other by showing them as circles.
200
∩ means?
It means the intersection of 2 sets.
A ∩ B , the intersection of A and B
200
Set A is the complement of Set B
A = {1, 3, 5, 7, 9}
B = {2, 3, 5, 7},
False
300
Define empty set
It is a set that contains no elements.
300
What is the intersection of a Venn diagram?
It is the elements that are in more than one set.
For example if you have set A and Set B, the intersection of A and B will contain the same elements of set A and Set B.
300
A = {1, 3, 5, 7, 9} and B = {2, 3, 5, 7},
what is A ∩ B?
{3, 5, 7}
300
If A = {1, 3, 5, 7, 9} and B = {2, 3, 5, 7},
what is A ∪ B?
{1, 2, 3, 5, 7, 9}
400
Define Complement of a Set.
The complement of a set such as set A is the set of all elements in the universal set that are not in set A. It is denoted as A'
400
What is the convention used when writing the elements of a set?
Chain brackets, commas, no duplicate elements
400
E = {0, 2, 4, 6, 8}
L = {0, 1, 2, 3, 4, 5, 6}
Write the intersection of sets E and L
E ∩ L = {0, 2, 4, 6}
400
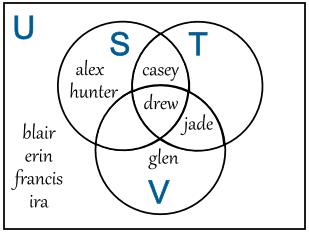
From the above Venn diagram, what is the set (S ∩ T)?
{casey, drew, jade, glen}
S ∩ T = {casey, drew}
500
Define Disjoint Sets
Two sets are said to be disjoint if they have no elements in common
500
How many circles are in the box of a Venn diagram?
Usually 2 but sometimes can be 1 or 3
500
The Universal Set = { The letters of the alphabet} and A = {vowels}.
What is the complement of A?
A'
A' = {the consonants}.
500
If
P = The set of whole numbers less than 5
R = The set of factors of 6
Then what is (P ∩ R)?
Last step (∩ means "intersection", must be in both sets):
(P ∩ R) = {1, 2, 3