Ratios
Proportions
AA/SSS/SAS Similarity
Similarity Statements
Special Segments of Similar Triangles
100
Describe a ratio.
"What is a comparison of two or more quantities set up like: a to b, a/b, a:b?"
100
Describe a proportion.
"What is an equation comparing to ratios."
100
According to SSS Similarity, what do two triangles need to have in order to be similar?
"What is three proportional, corresponding, sides?"
100
True or False?
A similarity statement must match corresponding angles.
"What is TRUE?"
A similarity statement must match both corresponding angles and proportional sides.
100
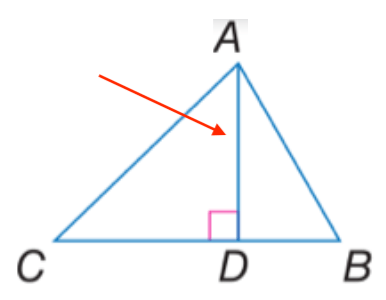
Name the indicated segment.
"What is an altitude?"
200
The ratio of vowels to total letters in the word: SUPERCALIFRAGILISTICEXPIALIDOCIOUS.
"What is 8:17?"
200
Solve for x.
14/84 = x/66
"What is x=11?"
200
State if the triangles are similar or not and then what similarity statement makes it so.
"What is YES, by AA Similarity?"
200
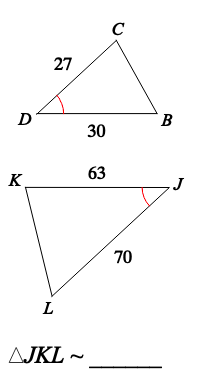
Complete the similarity statement.
"What is Triangle DCB?"
200
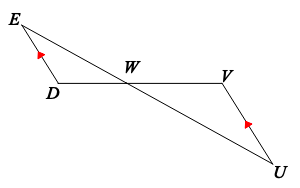
Name the indicated segment.
"What is a median?"
300
In a triangle, the ratio of the measures of the sides is 2:2:3 and the perimeter is 392 inches. Find the length of the longest side of the triangle.
"What is 168 inches?"
300
Given two equilateral triangles with sides 16 and 18, respectively, the scale factor of the larger triangle to the smaller triangle.
"What is 9 to 8?"
300
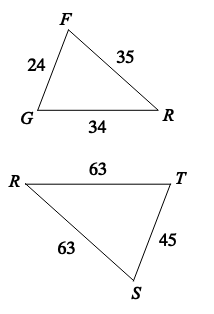
State if the triangles are similar or not and then what similarity statement makes it so.
"What is NO, not similar?"
300
Triangle ABC is similar to Triangle XYZ. Complete this statement: Triangle BCA is similar to..."
"What is Triangle YZX?"
300
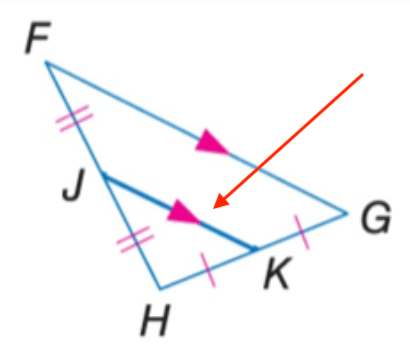
Name the indicated segment.
"What is a midsegment?"
400
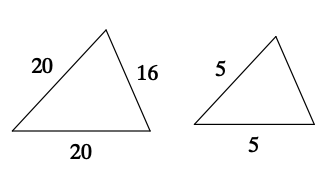The triangles are similar, find the scale factor of the larger triangle to the smaller triangle.
"What is 4:1?"
400
Given the two triangles are similar, find the missing indicated length.
"What is ? = 39?"
400
According to SAS Similarity, what do two triangles need to have in order to be similar?
"What is the lengths of two sides of one triangle proportional to the lengths of two corresponding sides of the other triangle and the included angles are congruent.?"
400
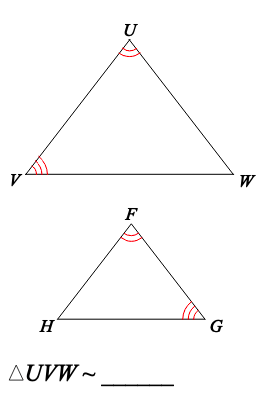
Complete the similarity statement.
"What is Triangle FGH?"
400
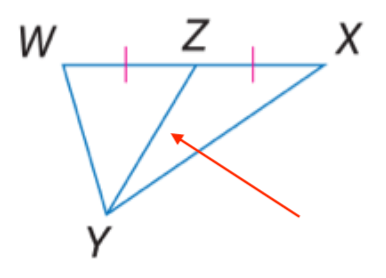
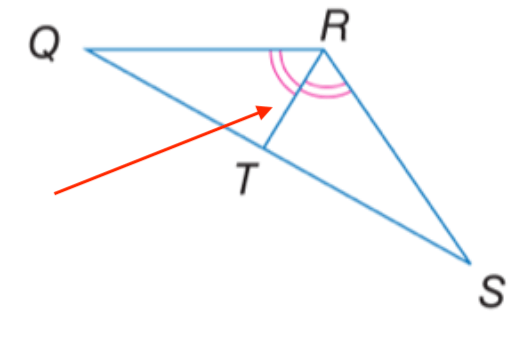Name the indicated segment.
"What is an angle bisector?"
500
The ratio of the measures of the sides of a triangle is 20:18:14. The perimeter of the triangle is 312. Find the lengths.
"What is 120, 108, and 84?"
500
Solve for x.
2/x=x/32
"What is x=8?"
500
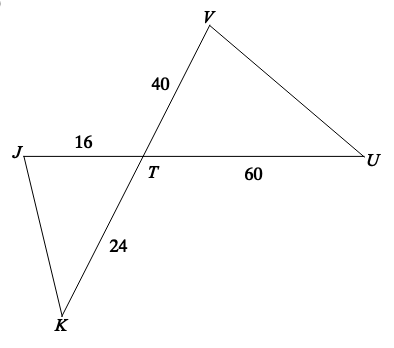
State if the triangles are similar or not and then what similarity statement makes it so.
"What is YES, by SAS Similarity?"
500
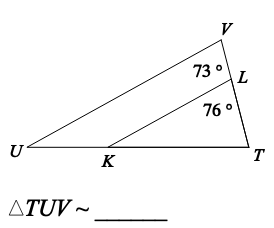
Are the triangles similar? If so, complete the similarity statement.
"What is NOT SIMILAR?"
500
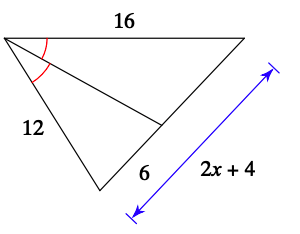
Given the angle bisector, solve for x.
"What is x=5?"