Theorems
Scale Factors
Proportions
Corresponding Parts
Miscellaneous
100
Does AA~ prove:
a) congruence
b) similarity
c) both
d) neither
b) similarity
100
What happens to a shape with a scale factor greater than 1?
It grows or gets bigger.
Enlargement
100
Solve the proportion
2/3=x/9
x = 6
100
Which side corresponds to BA?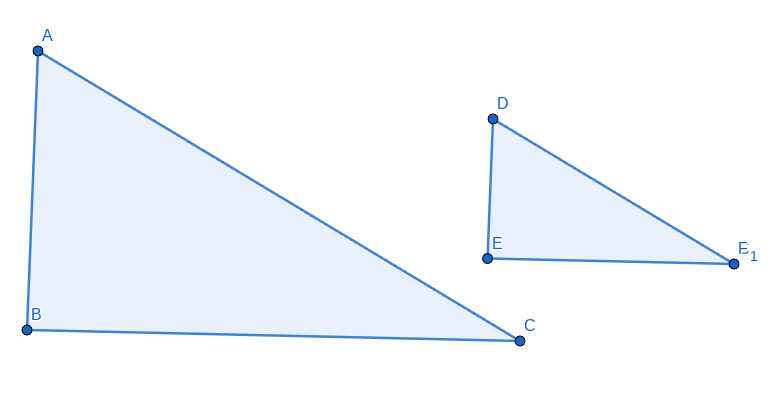
ED
100
If the scale factor is 2 (k = 2), what are the new ordered pairs?
A'(6, -4)
B'(8, 4)
C'(-4, 6)
D'(-8, 0)
200
Name three congruence theorems (last chapter - think triangles)
SSS
ASA
SAS
AAS
HL
200
What do you know about a scale factor that shrinks a shape?
It is less than 1 but greater than zero
(between zero and one)
example: 1/2, 3/4, .25 etc.
200
Solve the proportion
3/4=6/(x+2
x = 6
200
What angle corresponds to M?
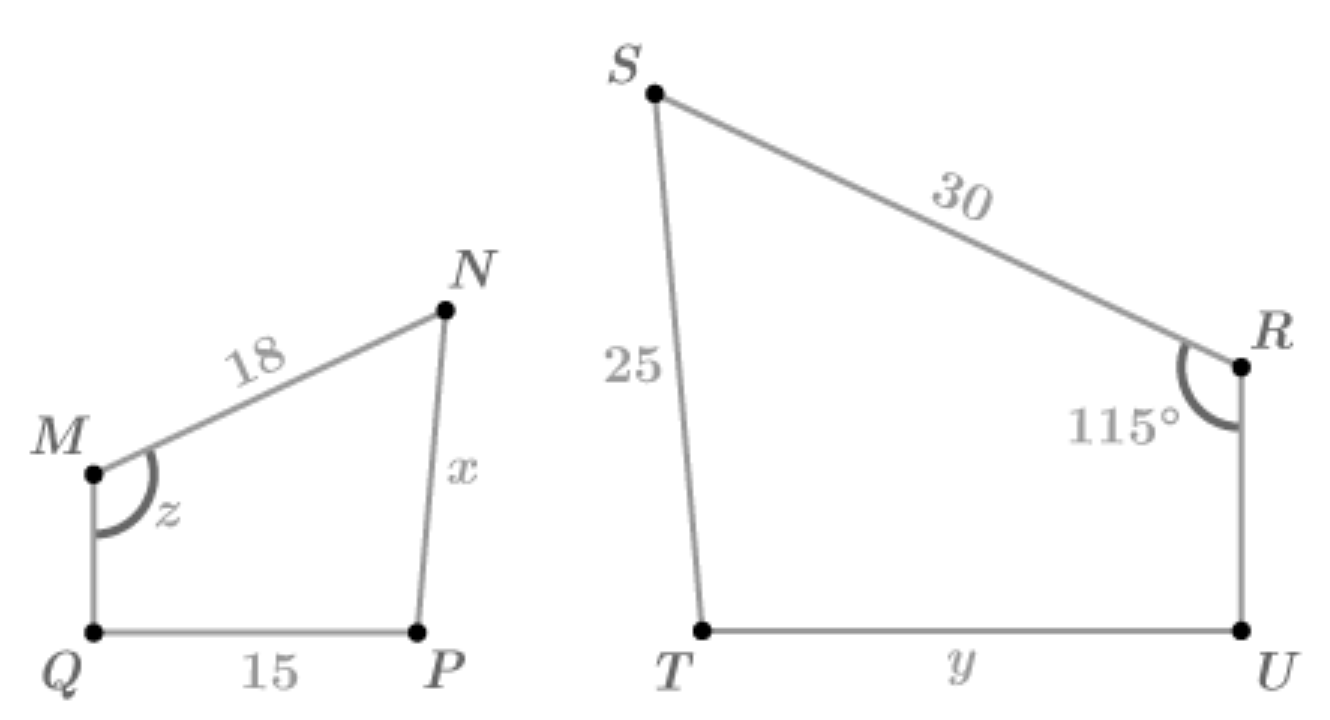
R
200
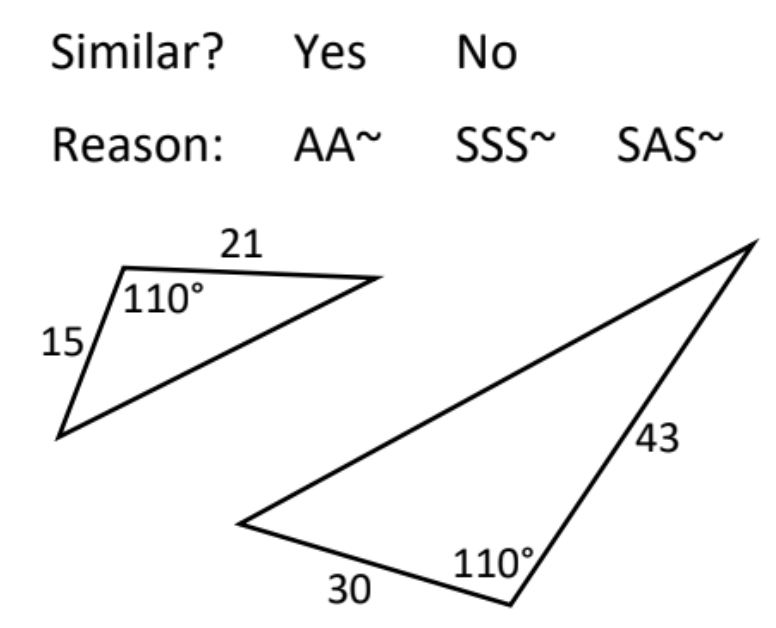
Not similar. Even though they have 1 angle in common, the 2 sides are not the same ratio.
300
Does SAS prove:
a) congruence
b) similarity
c) both
d) neither
c) both
300
What is the scale factor of triangle ABC to triangle ADE?
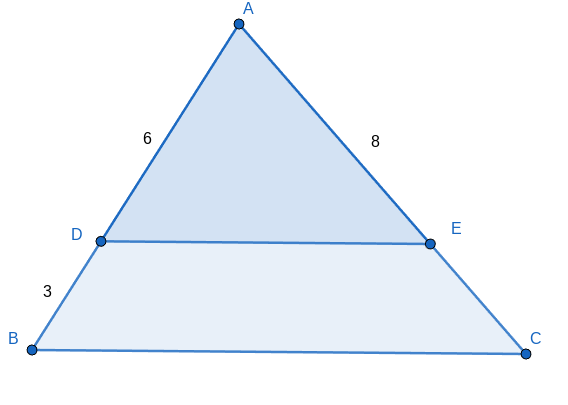
2/3
300
What proportion could you use to solve for x?
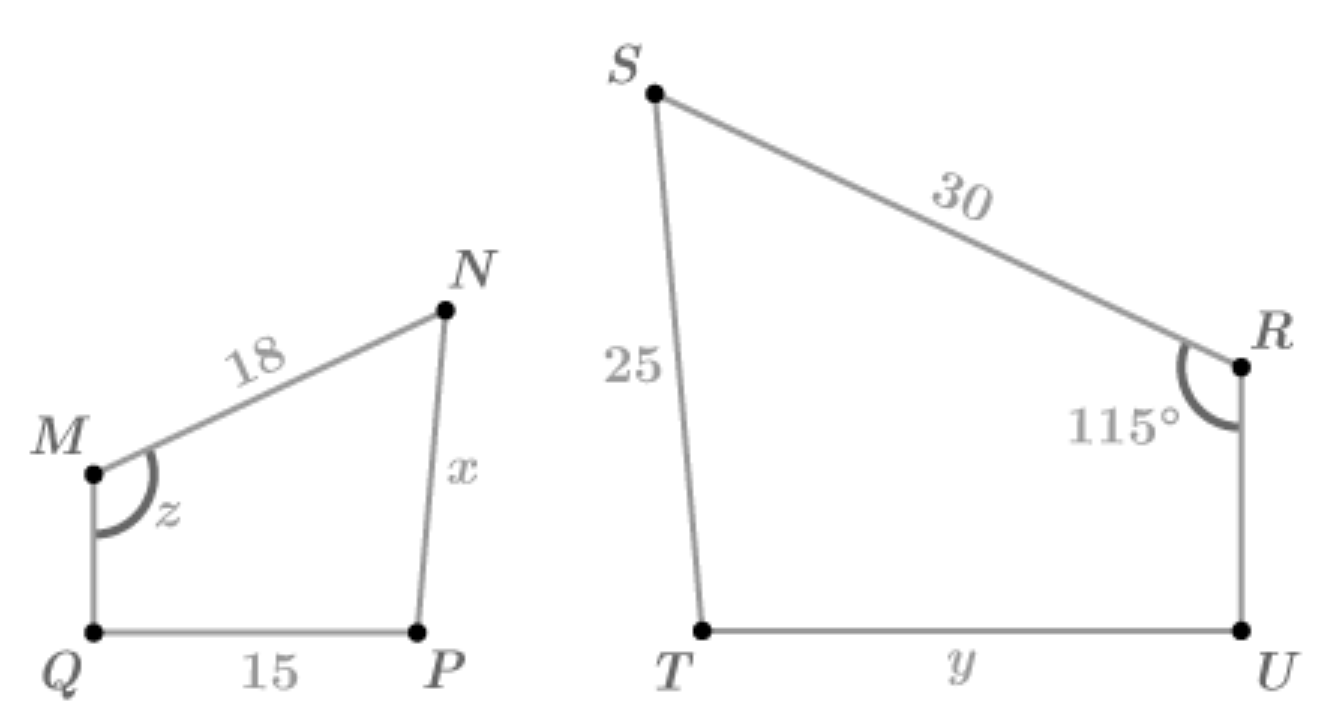
Teacher's discretion.
300
What side corresponds to CB?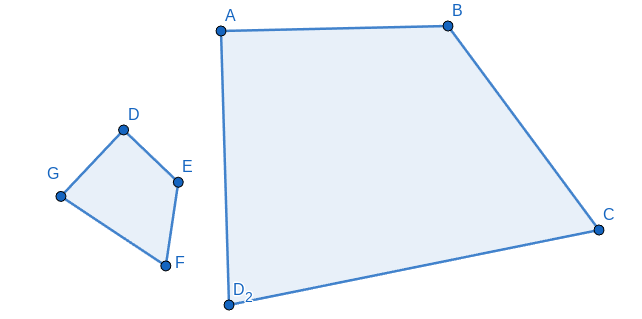
FE
300
What ratio could you use to solve for x?
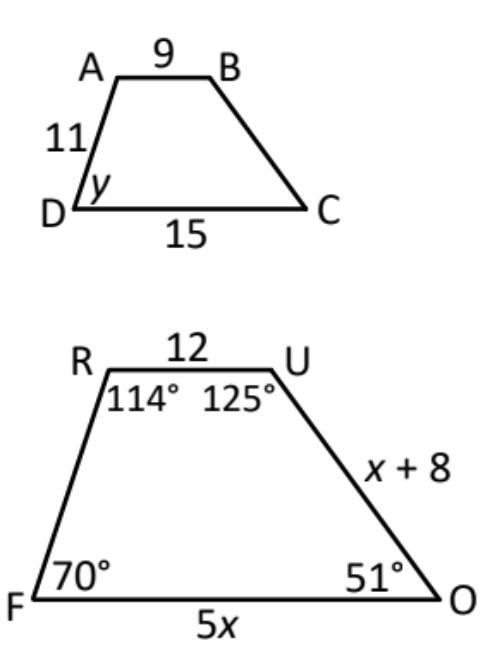
Teacher's Discretion
400
Are these triangles similar? If so, by what reason?
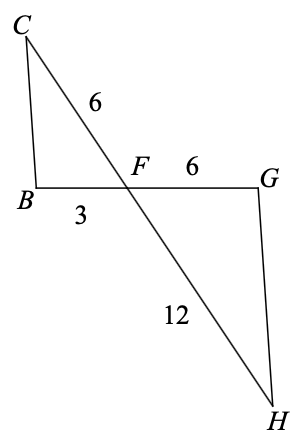
Sides are both in the ratio 1/2 and the vertical angle means they are similar by SAS~
400
A segment is 4 units long. It is dilated by a scale factor of 5/2. How long is the new segment?
10 units
400
Solve for ? in the picture
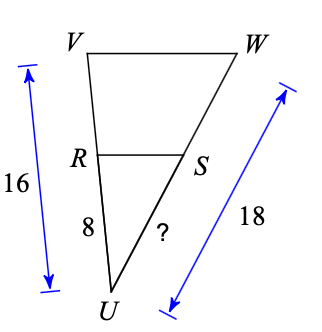
? = 9
400
What side corresponds to MN?
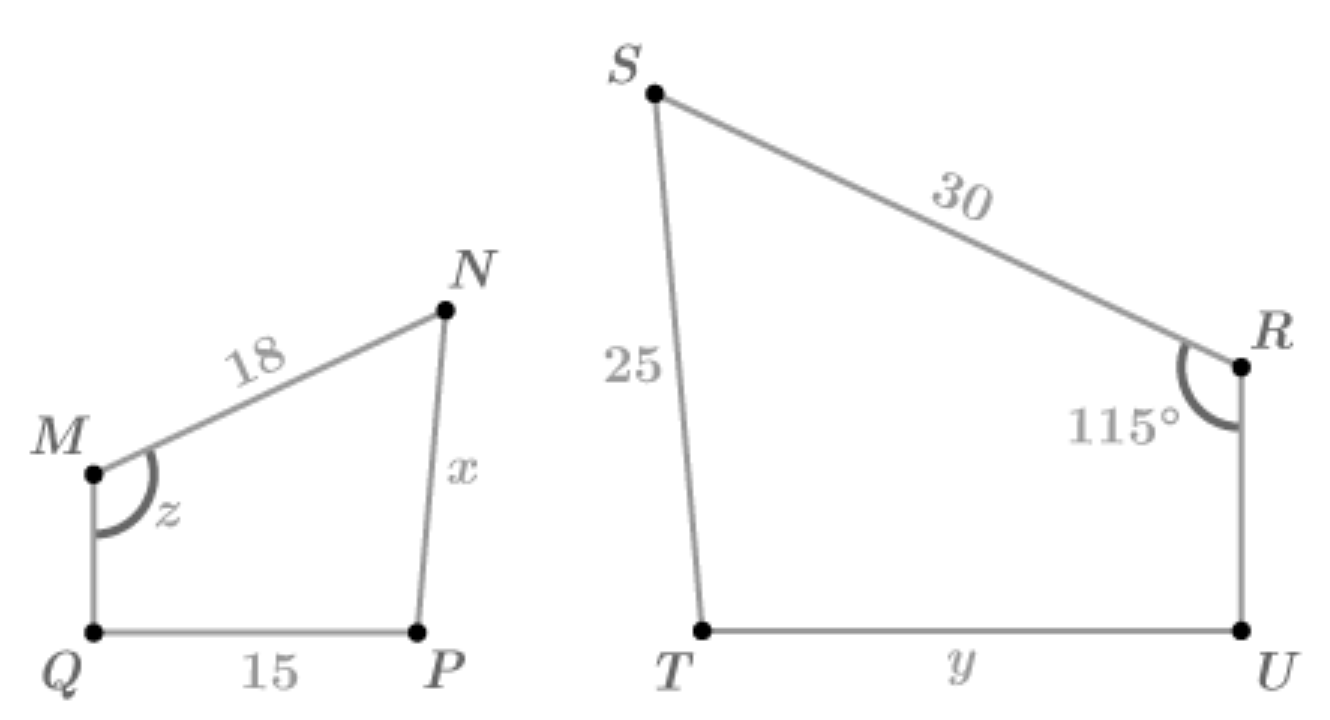
RS
400
Solve for x:
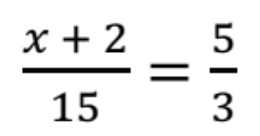
x = 23
500
How can you prove these triangles are similar?
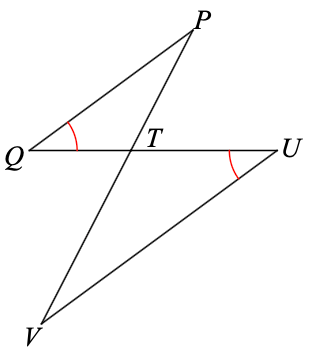
AA~
500
What will a scale factor of 1/4 do to the pre-image?
Made it smaller
Reduction
500
What proportion could be used to solve for x?
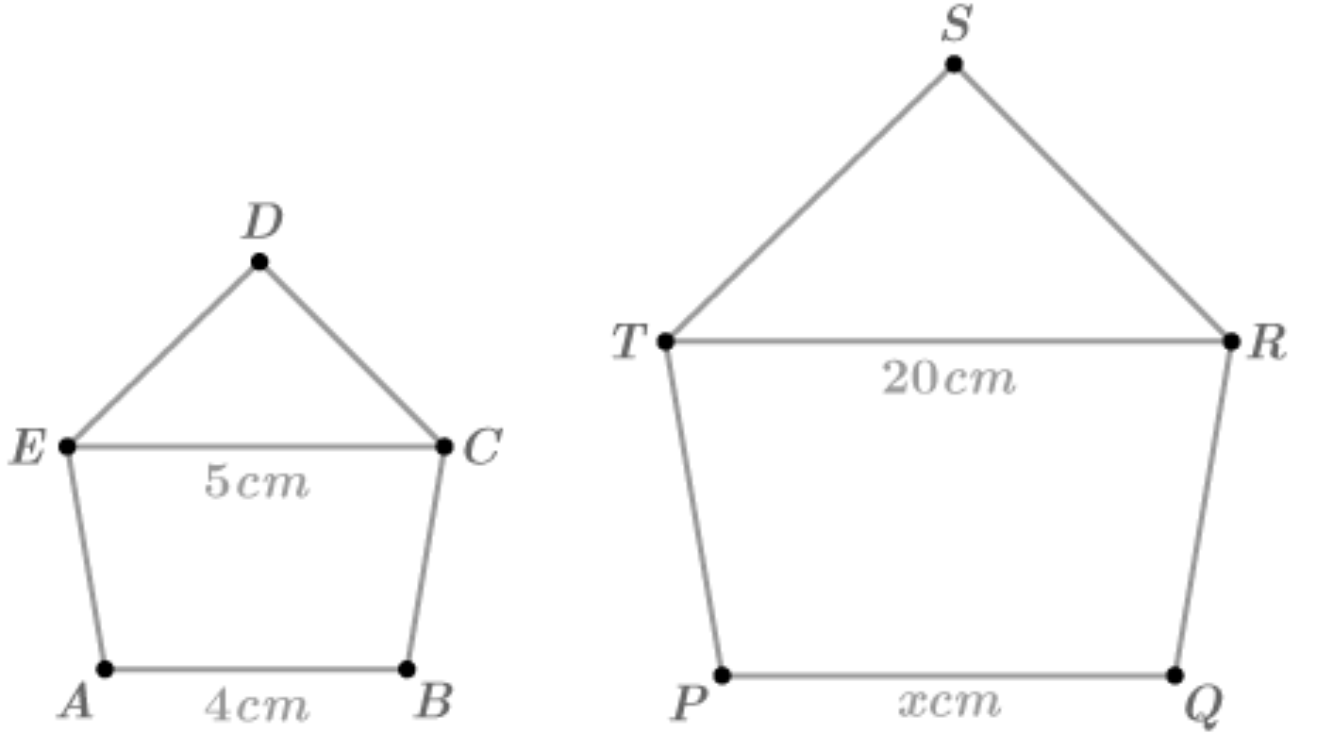
Teacher's Discretion
500
Name 2 sets of angles that are congruent in these similar triangles.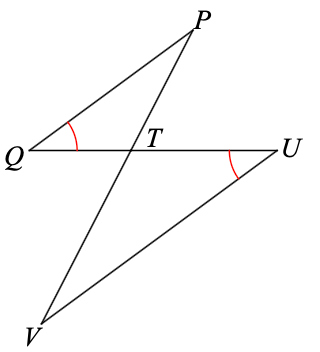
Angle Q and Angle U
Angle QTP and Angle UTV
500
If the scale factor is 1/3 (k = 1/3), what would the new ordered pairs be?
A'(2, -2)
B'(1, 2)
C'(-2, 1)