(Use a proportion)
In the diagram, ABC ~ A'B'C'. Find the value of AC.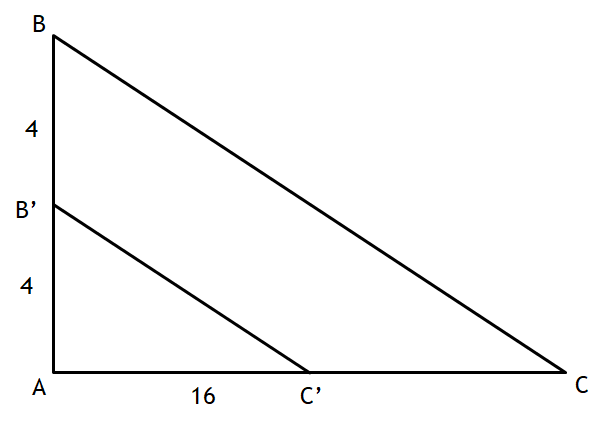
AC = 32
Are the following triangles similar? Justify your answer.
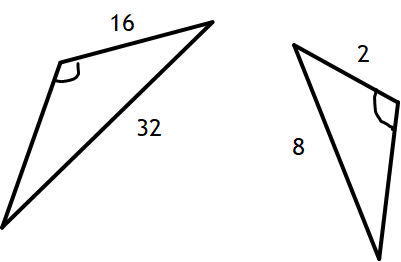
The corresponding side lengths are not in proportion. Therefore, the triangles are Not Similar.
_____________ means to have the same shape.
Similarity
Given:
AD and BC intersect at E
AB|| CD
Prove: ∆ABE ~ ∆DCE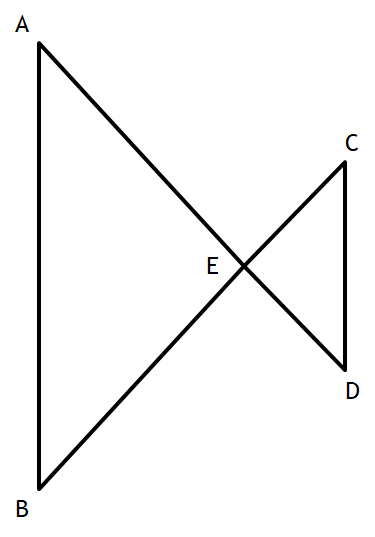
Statement Reason
1)AD and BC intersect 1) Given
at E
AB|| CD
2) <C ≅ <B 2) Alternate Interior
and <A ≅ <D <'s are ≅
3) <AEB ≅ <CED 3) Vertical <'s are ≅
4) ∆ABE ~ ∆DCE 4) AA(A)
If the sides of one triangle are 6, 8, 10 and the longest side of a similar triangle is 20. What is the length of the shortest side?
The shortest side is 12
Examine the figure below. Determine if the two triangles are similar. Justify your answer.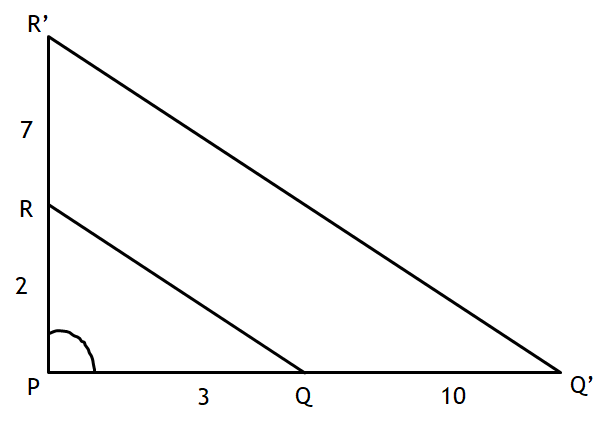
__________ means to have the same shape and size.
Congruent
Given:
AE and NL intersect at G
AN || LE
Prove: ∆AGN ≅ ∆LGE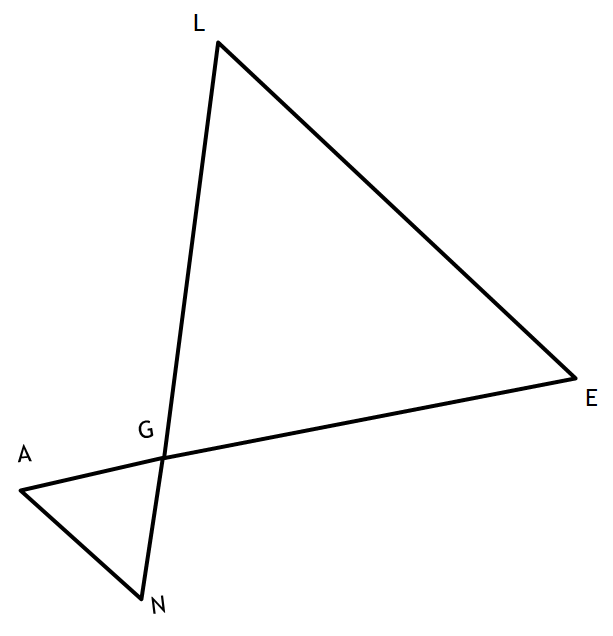
Statement Reasons
1)AE and NL intersect at 1)Given
G and AN || LE
2) <L ≅ <N 2) Alternate
and <E ≅ <A interior <'s are ≅
3) <AGN ≅ EGL 3) Vertical <'s are ≅
4)∆AGN ≅ ∆LGE 4) AA(A)
In the diagram, ∆ABC~∆EFG
<C = 120 degrees, <F = 15 degrees, AB=20, EF=10 and AC =8
a)Determine m<E.
b) Use a proportion to find the length of EG.
a) <E = 45 degrees
b) EG = 4
Find the missing side of these two similar triangles. 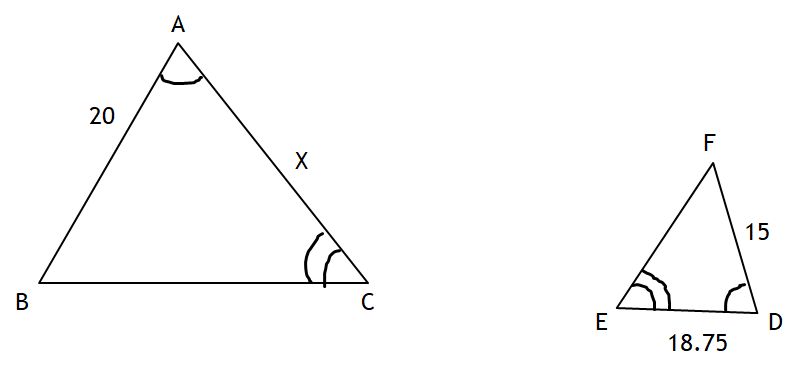
x = 25
AA(A): Two triangles are (1)__________ if two angles of one triangle are (2)____________ to two corresponding angles of the other triangle.
(1) Similar
(2) Equal
Given: ABDE is a trapezoid
AB || ED
Prove: ∆AFB~ ∆DFE
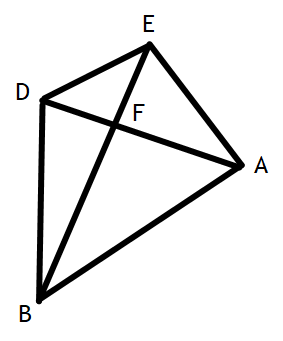
Statement Reason
1) AB|| ED 1) Given
2) <E ≅ <B 2) Alt. Interior <'s are ≅
3) <D ≅ <A 3)Alt. Interior <'s are ≅
4)<EFD ≅ <AFB 4) Vertical <'s are ≅
5)∆AFB~ ∆DFE 5) AA(A)
A flagpole cast a shadow 16.60 meters long. Tim stands at a distance of 12.45 meters from the base of the flagpole, such that the end of Tim's shadow meets the end of the flagpole's shadow. If Tim is 1.65 meters tall, determine and state the height of the flagpole to the nearest 10th of a meter.( Draw your picture first to help you)
The flagpole 6.6 is meters tall.
Triangles RST and XYZ are drawn below. IF RS=6, ST=14, XY=9, YZ=21, and <S ≅ <Y. is ∆RST similar to ∆XYZ? Justify your answer. 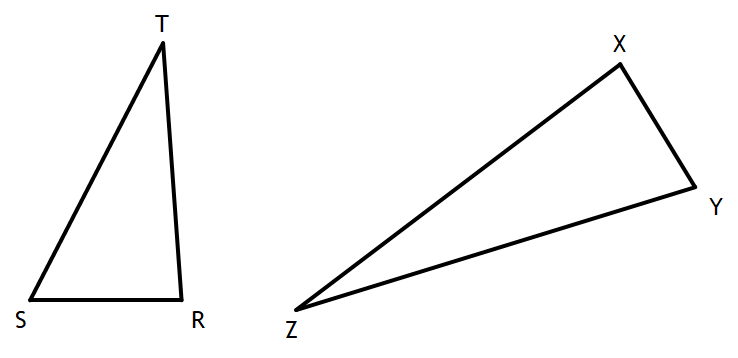
Yes, ∆RST is similar to ∆XYZ since the corresponding sides are in proportion.
SAS: Two triangles are (1)_________ if two pairs of corresponding sides are in (2)___________ and the angles between them are (3)_________.
(1) Similar
(2) Proportion
(3) Equal
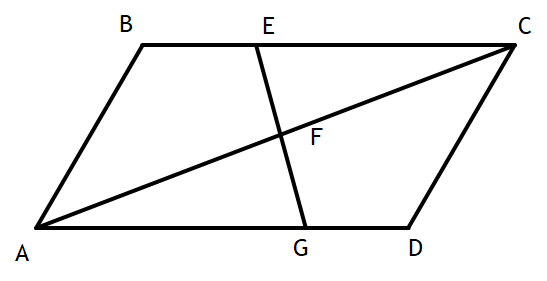
Given: ABCD is a parallelogram and AFC is the diagonal.
Prove ∆AFG ~∆EFC
Statement Reason
1) DFB is the diagonal 1) Given
2) EC || AG 2) ABCD is a
Parallelogram so the
opposite sides
are parallel.
3) < A ≅ <C 3) Alt. interior <'s
and <G ≅ <E are ≅
4) <CFE ≅ <AFG 4) Vertical <'s are ≅
5) ∆AFG ~∆EFC 5)AA(A)
A summer camp counselor wants to find a length, x, in ft. across a lake represented in the picture below. The lengths represented by AB, EB, BD, and CD on the sketch were determined to be 1800 ft, 1400 ft, 700 ft, and 800 ft respectively. Segments AC and DE intersect at B, and <AEB and <CDB have the same measure. Use a proportion to determine the value of x. 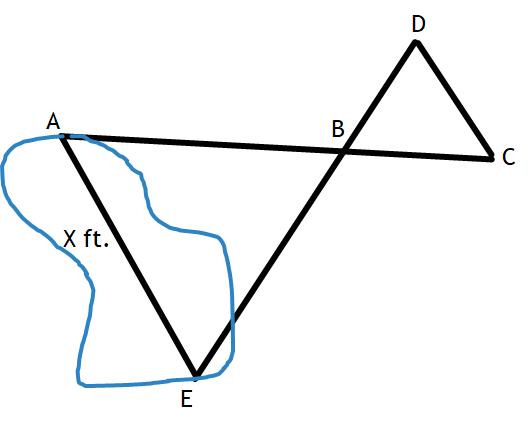
x = 1600 ft
In the diagram below ΔABC~ ΔDEC. If AC = 12, DC =7, DE =5, and the perimeter of ΔABC is 30. What is the perimeter of ΔDEC?
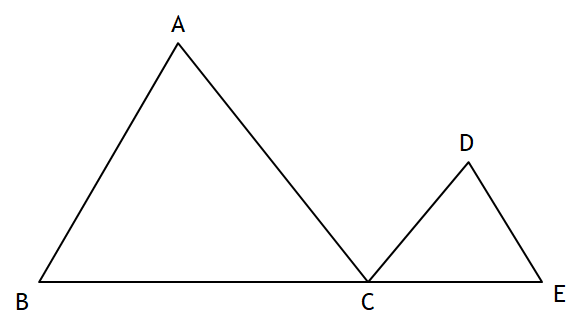
The perimeter is 17.5
(1)Similar
(2) sides
(3) Proportion
Given: GI || NT
IN intersects GT at A
Prove: ∆GIA ~ ∆TNA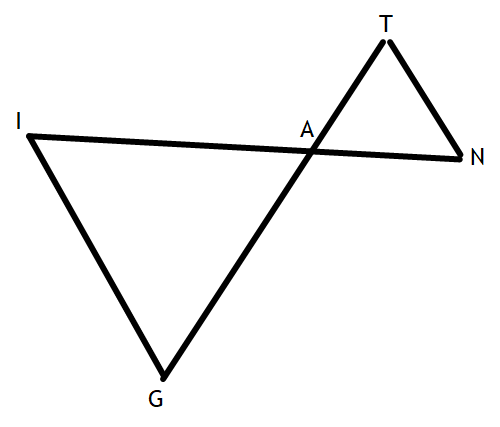
Statements Reasons
1.) GI || NT 1) Given
IN intersects GT at A
2.)<I ≅ <N 2) Alt. Int. <'s are ≅
3.) <G ≅ <T 3) Alt. Int <'s are ≅
4.) <IAG ≅ <TAN 4) Vertical <'s are ≅
5.) ∆GIA ~ ∆TNA 5) AA(A)