SAS, SS, AA
Proportions in Similar Triangles
Similar?
Proportions pt. 2
Surprise
100
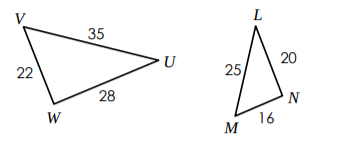
According to SSS Similarity, what do two triangles need to have in order to be similar?
All sides are proportional
100
This is the value of q.
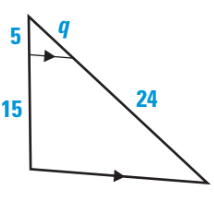
8
100
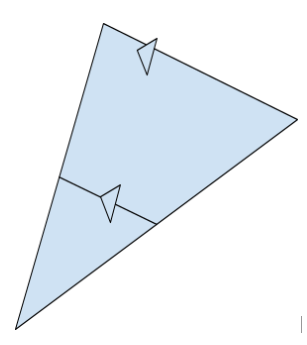
Are these triangles similar?
Yes
100
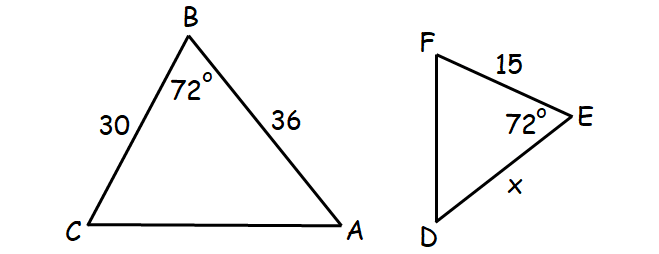
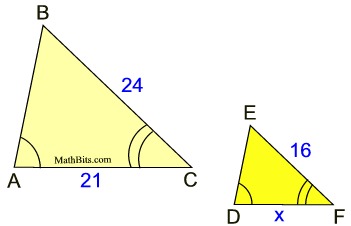
Find DE
18
100
What is congruent in similar triangles?
Angles
200
This similarity theorem allows us to conclude that the two triangles are similar.
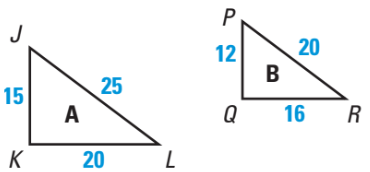
SSS
200
This is the value of p.
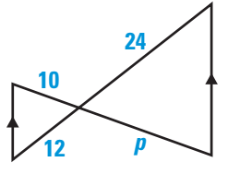
20
200
Are these similar?
No
200
12
200
The following triangles are similar. Find the missing side.
14
300
This is the similarity theorem that allows us to conclude that the triangles are similar.
SAS
300
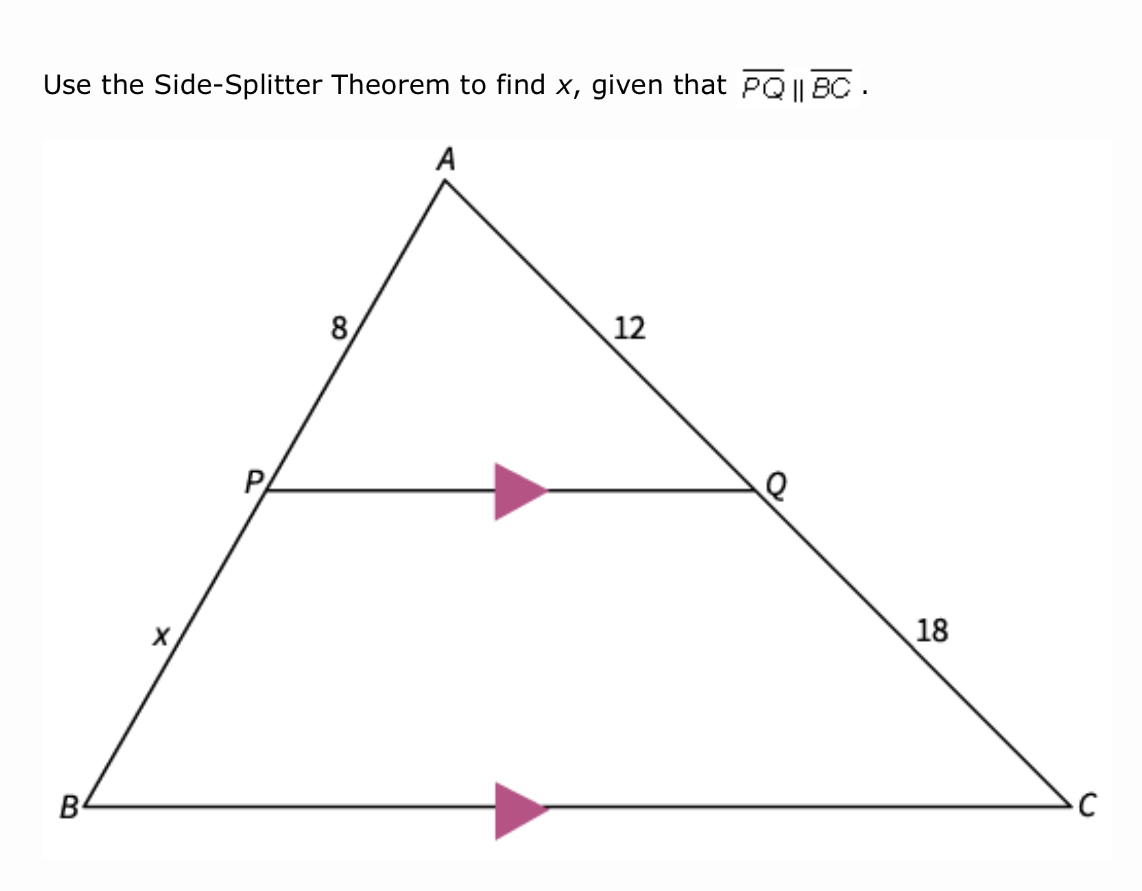
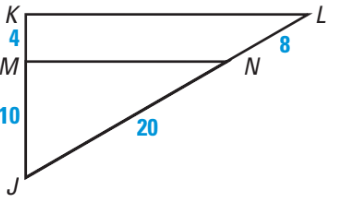
Solve for x.
6
300
What is the reasoning for #3?
AA
300
Find AB
x=16
AB=40
300
Solve for x. The triangles are similar.
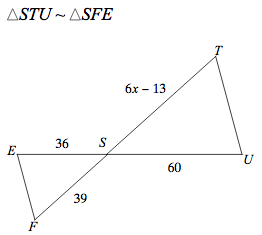
13
400
State if the triangles are similar or not and then what similarity statement makes it so.
AA
400
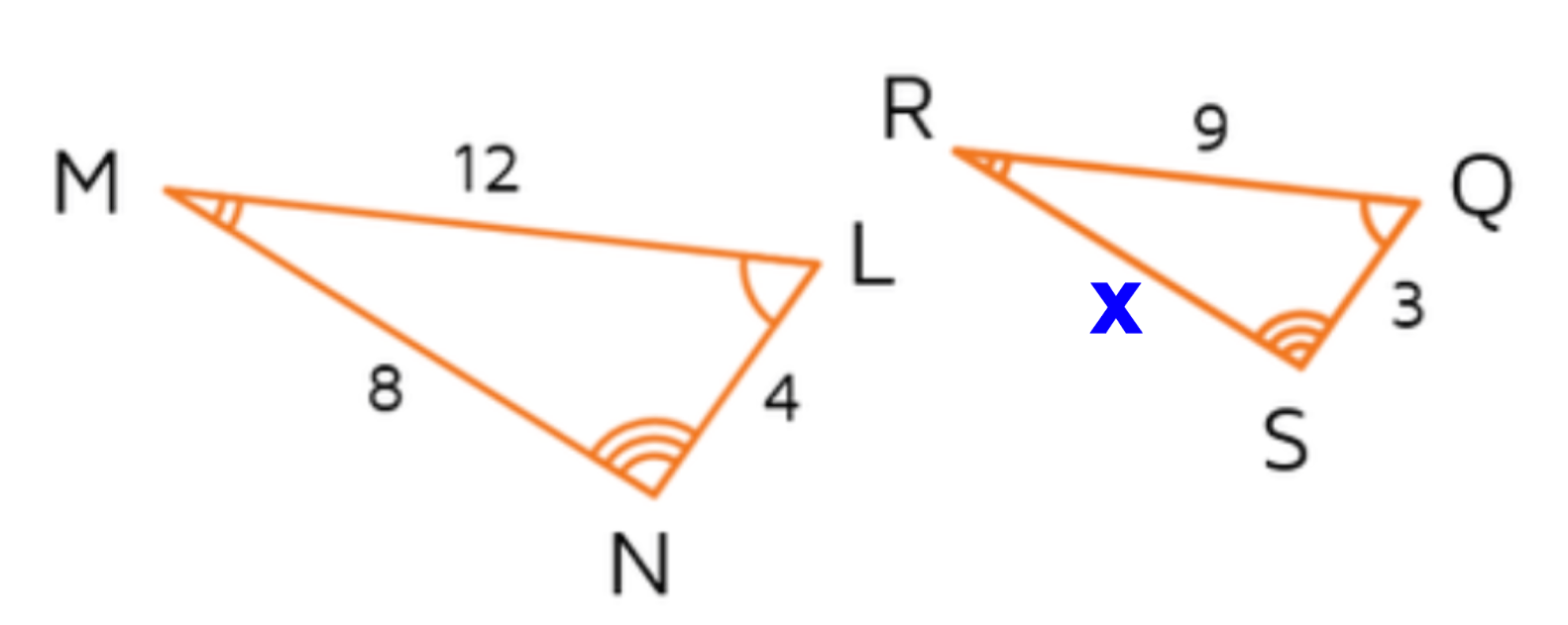
Solve for x.
11
400
This is a correct similarity statement for these two triangles.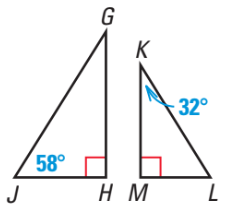
Triangle JGH is similar to triangle LKM
400
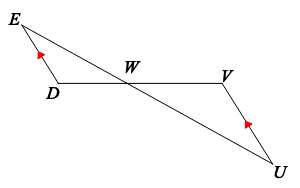
Solve for x.
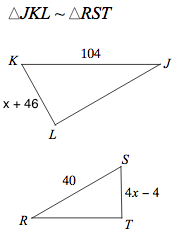
6
400
If triangle ABC ~ triangle XYZ by a scale factor of 1/3 YZ=?
4
500
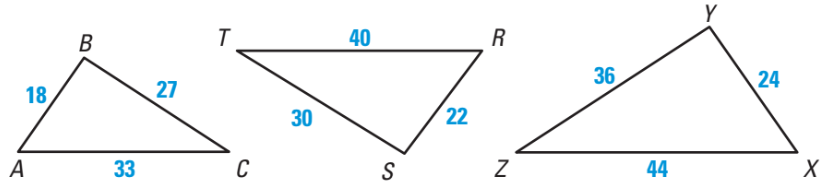This is the triangle that is similar to
△ABC.
XYZ
500
Solve for y.
9
500
In triangles ABC and XYZ, angle A = angle X, AB =10, XY = 24, AC = 5 and XZ = 12. Are the triangles similar, Write the similarity statement and reason.
ABC is similar to XYZ by SAS
500
How tall is the person? (feet, inches)
4 ft 4 inches
500
DE || AB
x=?
9