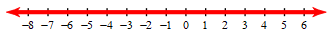Solve \frac{|x-2|}{6}=4 .
x= 26,-22
Solve and graph 9+|-m+4|\geq14
(-\infty,-1] \cup [9,\infty)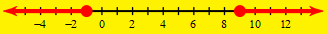
What is the formula when writing an absolute value equation from a scenario?
|x-mean|=distance
What is the formula for writing an absolute value inequality from a scenario?
|x-mean|\leq deviation
Graph the following interval and write it in interval notation.
-4<a<6
(-4,6)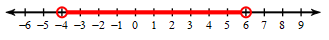
Solve |\frac{n}{4}|-2=-5
No solution.
Solve and graph \frac{|4m-9|}{-7}<5
All real numbers
(-\infty, \infty)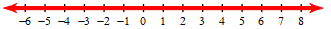
The minimum height requirement for the military is 55 inches while the maximum height for the military 80 inches. Write an absolute value equation to represent this scenario.
|x-67.5|=12.5
A cereal box has an average weight of 20 grams with an absolute deviation of 0.75 grams. Write and solve an absolute value inequality to represent the possible ranges for this scenario.
|x-20|\leq0.75
[19.25,20.75]
Graph the following interval and write it in interval notation.
-5\leqn\leq\frac{1}{3}
[-5,\frac{1}{3}]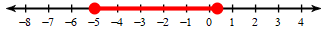
Solve 2|5-x|+1=5 .
x=3, 7
Solve and graph 8|-9+6n|-4<20
(1,2)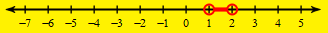
The minimum number of points scored on a test was 54 and the maximum number of points scored a test was 100. Write an absolute value equation to model this scenario.
|x-77|=23
You are able to go 9mph within the speed limit of 65mph without getting a ticket. Write and solve an absolute value inequality to represent the range of value for this scenario.
|x-65|\leq9
[56,74]
Graph the following interval and write it in interval notation.
m>4 or m<-2
(-\infty,-2)\cup(4,\infty)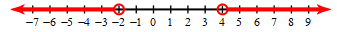
Solve 6-6|6-2x|=30 .
No solution
Solve and graph 2-6|-5k-8|\geq80
No solution
The minimum height for a dog is 10 inches while the maximum height is 15 inches. Write an absolute value equation to model this scenario.
|x-12.5|=2.5
Pumpkins at a pumpkin patch weighed 20, 23, 24, 26, 22 pounds. Mr. Yohn only wants to keep pumpkins that are within 2 pounds of the average weight. Write and solve an absolute value inequality to determine the range of values.
|x-23|\leq2
[21,25]
Graph the following interval and write it in interval notation.
n\leq-1 or n\geq0
(-\infty, -1) \cup (0,\infty)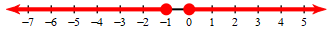
Solve |p+8|=3p+8
p= 0
Solve and graph -4-3|-8v-4|<-88
(-\infty,-4)\cup(3,\infty)
The minimum number of days off for Winter Break could be 5 days while the maximum number of days off for Winter Break could be 12 days. Write an absolute value equation to represent this scenario.
|x-8.5|=3.5
The temperatures for the past seven days are 65, 70, 75, 68, 62, 71, 73 degrees Fahrenheit. The gym classes can only go outside if it is within 3 degrees of the average temperature. Write and solve an absolute value inequality to represent the range of values for this scenario.
|x-69|\leq3
[66,72]
Write the following solution in interval notation and graph the solution.
All real numbers
(-\infty, \infty)