Factoring
Taking the Square Root
Completing the Square
Quadratic Formula
Complex Numbers
100
Solve for the zeros
4x(2x + 1) – 3(2x + 1) = 0
x = -1/2 & x = 3/4
100
Solve for the zeros by taking the square root
x2 = 100
x = –10 & x = 10
100
Find the value of c that completes the square
x2 – 10x + c
25
100
If the discriminant is 0, describe the number and type of solutions.
One real solution
100
Simplify
(–6 – 8i) + (4 + 6i)
–2 – 2i
200
Write the following in factored form
x2 – 6x – 7 = 0
(x + 1)(x – 7)
200
Solve for the zeros by taking the square root
x2 = –81
x = 9i & x = –9i
200
Write as a binomial squared
x2 + 8x + ___
(x + 4)2
200
Find the discriminant and the number/type of solutions. *must be set = to 0*
–4x2 + 6x – 14 = –4
-124, two imaginary
200
Simplify
(–3 – 3i) – (6 – 8i)
–9 + 5i
300
Solve for the zeros by factoring
x2 – 3x + 2 = 0
x = 1 & x = 2
300
Solve for the zeros by taking the square root
36x2 – 3 = 33
x = 1 & x = –1
300
Solve for the zeros by completing the square
x2 + 8x – 15 = –6
x = 1 & x = –9
300
Solve for the zeros by quadratic formula
6x2 - x - 100 = 0
x = –4 & x =
25/6
or 4.2
300
(8i) – 4 – (–5 – i)
1 + 9i
400
Write the following in factored form
4x2 – 18x + 8 = 0
2(2x – 1)(x – 4)
400
Solve for the zeros by taking the square root
6(2x + 3)2 = 216
x = 3/2 & x = -9/2
or x = 1.5 & -4.5
400
Solve for the zeros by completing the square
x2 – 18x + 91 = 0
400
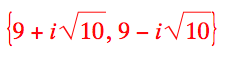
Solve for the zeros by quadratic formula
7x2 + 9x + 6 = 0
400
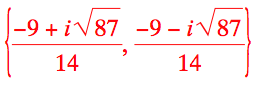
(–1 – i)(–7 – 4i)
3 + 11i
500
Solve for the zeros by factoring
x2 +10x +24 = 8
x = -2, -8
500
Solve for the zeros by taking the square root
2(5x – 1)2 + 7 = –25
(1+4i)/5 and (1-4i)/5
500
Solve for the zeros by completing the square
7x2 + 14x – 24 = –3
x = 1 & x = –3
500
Solve for the zeros by quadratic formula
3x2 – 72 = 6x
x = 6 & x = –4
500
(-3-9i)/(3+i)
(-9-12i)/(5)