Solutions
Solving Systems: Graphing
Solving Systems: Substitution
Solving Systems:
Elimination
Elimination
Word problems
100
3) after solving a system of linear equations you end with 5 = 8, how many solutions did the system of linear equations have?
zero
100
9)
What is the solution to the system of linear equations?
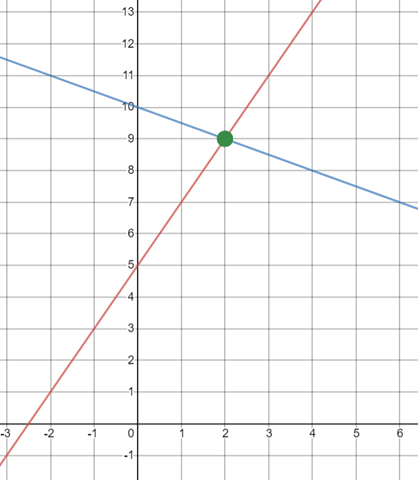
(2,9)
100
11) When should you use the substitution method to solve a system of linear equations?
when you know the value of one of the variables but not both variables. Example:
x = 4 + y
3y + x = 6
100
16) What is the first step when using the elimination method?
Create a zero pair
100
21) A collection of 20 coins consisting of 5-cent and 10-cent pieces and has a total value of $4.25.
What are your let statements?
Let x = number of 5-cent pieces
let y = number of 10-cent pieces
200
2) How many solutions does a graph have that intersects once?
one
200
10)
What is the solution to the system of linear equations?
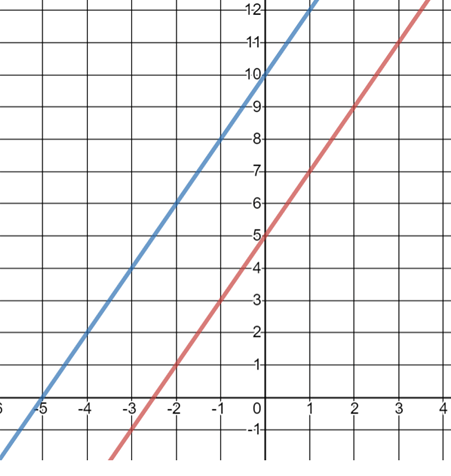
No solutions
200
12)
What is the solution to the system of linear equations?
5x+2=y
x=2
(2,12)
200
17)Solve the system of linear equations using the elimination method
4x+3y=12
2x-3y=24
(6,-4)
200
You attend an Eagles game. At the first food stall, the price of nachos is $4 and a beverage is $2 and you spent $12. At another food stall the price of nachos is $2 and a beverage is $1 and you spent $8. Write a system to represent both food stalls.
4n+2b=12
2n+b=8
300
4) How many solutions can a system of linear equations have?
0, 1 or infinitely many
300
Find the solution to the following system
y= x - 2
y=-2x +1
(1,-1)
300
13) What is the solution to the system of linear equations?
y = 2x
x + y = 24
(8,16)
300
18)
Solve the System of Linear Equations using the Elimination Method:
4x+3y=12
2x-3y=24
(6, -4)
300
At a basketball game, all tickets are the same price and all souvenirs are the same price. Bobby bought 2 tickets to this basketball game and 1 souvenir for a total of $17.25. Emily bought 5 tickets to the same game and 2 souvenirs for a total of $42.00. Set up a system of linear equations for this situation.
2t + s = 17.25
5t + 2s = 42
400
How many solutions does the following system of linear equations have?
x + 2y = 10
2x + 4y = 20
infinite
400
What is the solution to the following system of linear equations?
y = x - 7
y + x = 3
(5,-2)
400
14)
What is the solution to the system of linear equations?
5x+4y= 32
y=-9+3x
(4, 3)
400
19)
What is the solution to the system of linear equations?
6x+5y=4
-6x+7y=20
(-1,2)
400
The cost of three notebooks and four pencils is $8.50.
The cost of five notebooks and eight pencils is $14.50.
Determine the cost of one notebook and the cost of one pencil.
One notebook costs $2.50 and one pencil costs $0.25.
500
Determine how many solutions the following system has.
y=-x+3
y=-x+5
NO solutions
500
What is the solution to the following system of linear equations?
y=(1/2)x - 2
y=4x+5
(-2,-3)
500
15)
What is the solution to the system of linear equations?
2x – 3y = –2
y = –4x + 24
(5, 4)
500
20)
What is the solution to the system of linear equations?
2x+2y=-2
3x-2y=12
(2, -3)
500
A farmhouse shelters 10 animals. Some are pigs and some are ducks. Altogether there are 36 legs.
How many of each animal are there?
8 pigs and 2 ducks