Translating
Reflecting
Rotating
Dilating
100
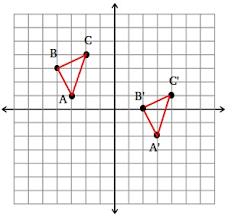
What is the transformation that maps ABC to A'B'C'?
The transformation that maps ABC to A'B'C' is a translation of 6 units to the right and 3 units down.
(x, y) ----> (x + 6, y - 3)
100
Reflect across the x -axis. Where would the coordinates of D' be?
The coordinates of D' would be (1, -2).
100
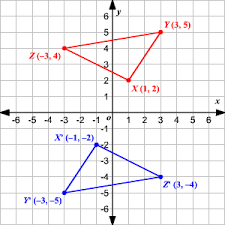
How was the triangle transformed?
The triangle was transformed by a rotation of 1800 about the origin.
100
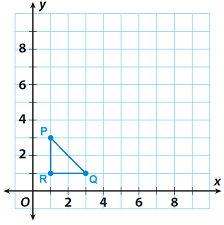
What would the coordinates of R' be if the triangle is dilated by a scale factor of 5.
The coordinates of R' would be (5,5) if the triangle were dilated by a scale factor of 5.
200
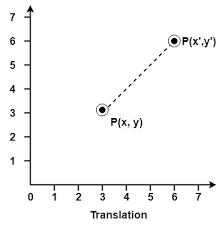
How can the transformation that maps point P to P' be best described?
The transformation that maps point P to P' is can be best described as a translation of 3 units to the right and 3 units up.
(x, y) ----> (x + 3, y + 3)
200
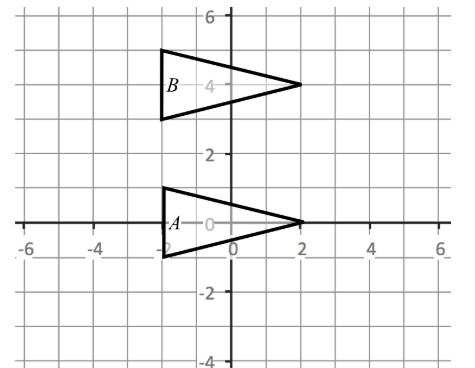
What is the line of reflection that maps A onto B?
The line of reflection that maps A onto B is the line y = 2.
200
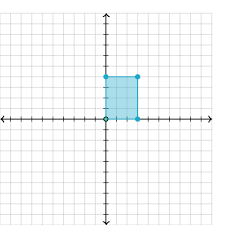
If we perform a rotation of 900 CCW about the origin, in which quadrant will the quadrilateral be?
If we perform a rotation of 900 CCW about the origin, the quadrilateral will be in quadrant II.
200
What's the scale factor that maps the original to the copy?
The scale factor that maps the original to the copy is 3.
300
How should the yellow triangle be moved to be mapped to the blue triangle?
The yellow triangle should be translated 12 units to the left and 12 units down to be mapped to the blue triangle.
(x, y) ---> (x - 12, y - 12)
300
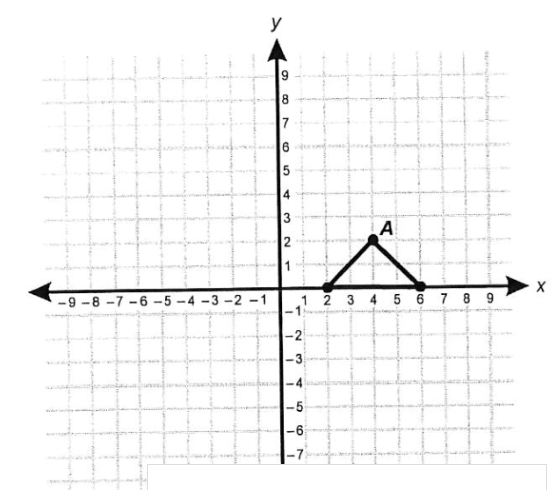
If the triangle were reflected across the line x = -2, in which quadrant would the triangle be?
If the triangle were reflected across the line x = -2, the triangle would be in quadrant II.
300
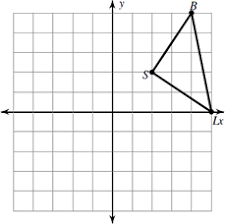
If you rotate triangle BLS 900 CW about the origin, what would the coordinates of B' be? (axes are scaled by 1)
If you rotate triangle BLS 900 CW about the origin, the coordinates of B' would be (5,-4).
300
What's the scale factor that maps the pre-image to the image?
The scale factor that maps the pre-image to the image is 1/2.
400
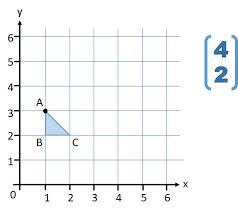
If we would perform a translation of the following rule, (x, y) ---> (x + 4, y + 2), what would be the coordinates of A'?
If we would perform a translation of the following rule, (x, y) ---> (x + 4, y + 2), the coordinates of A' would be (5, 5).
400
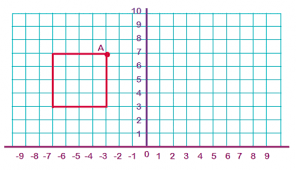
If we perform a reflection across the y-axis, where would the coordinates of A' be?
If we perform a reflection across the y-axis, the coordinates of A' would be at (3, 7).
400
How can the transformation be described?
The transformation can be described as a rotation of 900 CCW or 2700 CW about the origin.
400
If you dilate ABC by a scale factor of 1/3, what would the coordinates of C' be?
If you dilate ABC by a scale factor of 1/3, the coordinates of C' would be (1, 1).