What is the name of this symbol?
√
Radical or Square Root
Find the value of the hypotenuse of a right triangle when one leg is 3, and the other leg is 4.
5
Classify the triangle as acute, obtuse, or right if the length of the sides are 3, 4 and 5.
Right Triangle
What do we multiply the legs by to find the hypotenuse?
√2
What do you multiply the SL of the triangle by to get the hypotenuse?
2
You cannot leave a radical in the _________ of a fraction?
Denomenator
Find the value of the missing leg of a right triangle when the hypotenuse is 13 and one leg is 5.
12
Classify the triangle as acute, obtuse, or right if the length of the sides are 10, 11, and 20.
Obtuse Triangle
Find the value of the hypotenuse?
Legs=2
Hypotenuse=2√2
What do you multiply the SL by to get the measure of the LL?
√3
What is the name of this?
a2+b2=c2
Pythagorean Theorem
The value of c.
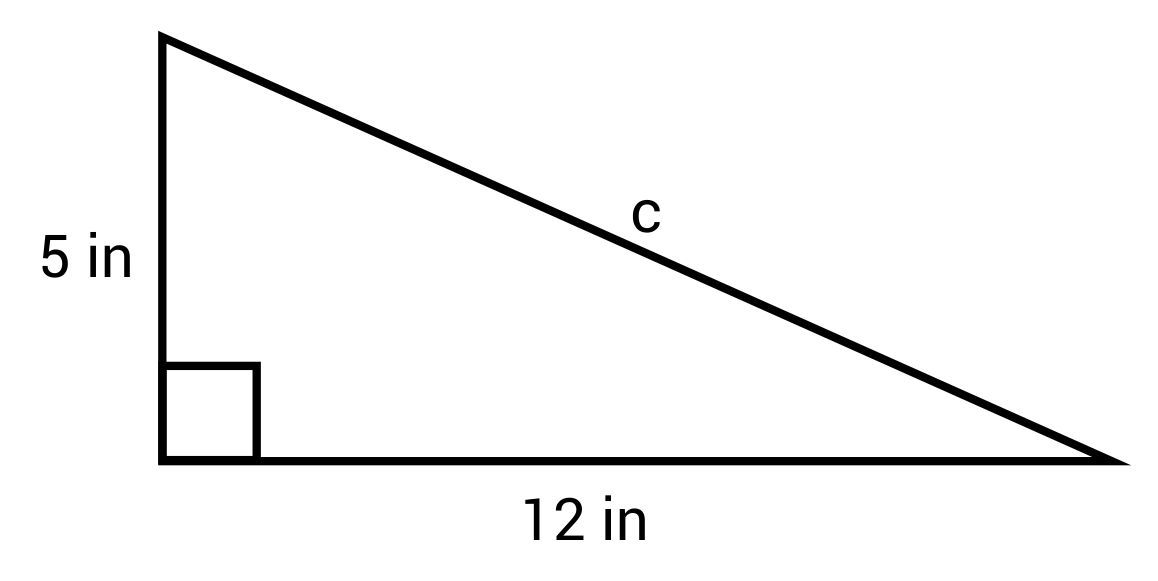
13 in
Classify the triangle as acute, obtuse, or right if the length of the sides are 73, 97 and 65.
Acute Triangle
The value of c.
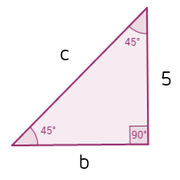
c=5√2
Find the value of g.
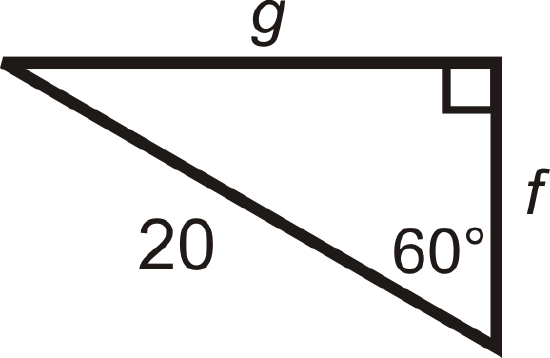
g=10√3
On a 45-45-90 triangle, what are the labels we use to label the legs and the hypotenuse?
Legs: a
Hypotenuse: a√2
The value of x to the nearest tenth.
14.7
Classify the triangle as acute, obtuse, or right if the length of the sides are 7, 2 Radical 15, 11.
Obtuse Triangle
Determine the length of the leg of 45°–45°–90° triangle with a hypotenuse length of 19.
a=(19√2)/2
Find the length of the hypotenuse of a 30°–60°–90° triangle with a long leg length of 15.
Hypotenuse= 10√3
On a 30-60-90 triangle, what are the labels we use to label the Short Leg, Long Leg, and Hypotenuse?
SL: a
LL: a√3
Hyp: 2a
The bottom end of an 11-foot ramp at a warehouse is 10 feet from the base of the main dock. Find the height of the dock? Round your answer to the nearest tenth.
4.6 ft
If the numbers represent the lengths of the sides of a triangle. Classify the triangle as acute, obtuse, or right.
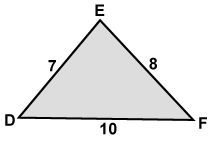
Acute Triangle
What is the value of a?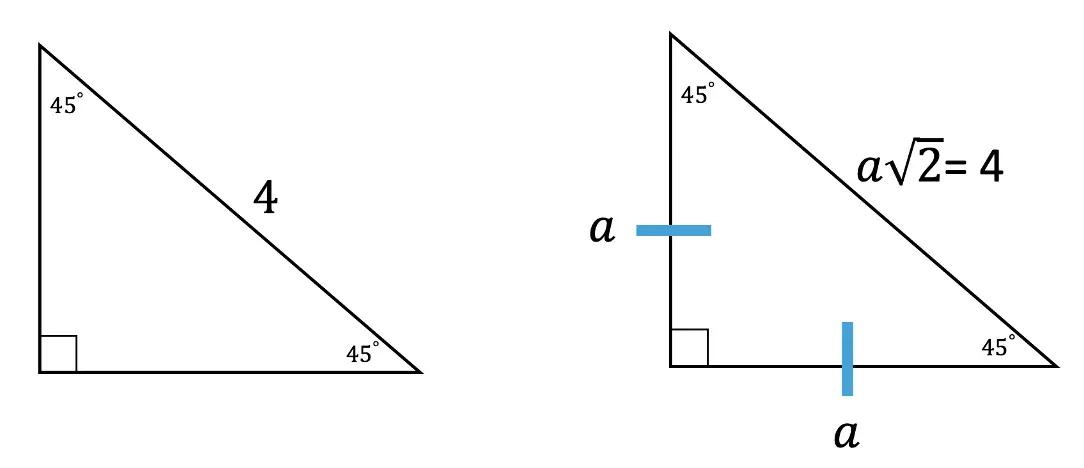
a=2√2
An equilateral triangle has an altitude of 15 feet. Determine the length of both the SL and the Hypotenuse.
SL=5√3
Hypotenuse: 10√3
