Derivatives
Marginal Analysis
Linear Approximation
Critical points
Graphing Characteristics
100
Given the following information and
h(x)=f(g(x))
, compute h'(3).
g(3)=2, f'(2)=6, g'(3)=5
h'(3)=30
100
What is marginal analysis? What does it show us?
A way of approximating the change associated with increasing production by ONE unit.
C(x+1) - C(x) = Cost to produce one more item
R(x+1) - R(x) = Revenue from selling one more item
P(x+1) - P(x) = Profit from selling one more item
100
If the second derivative is POSITIVE, the linear approximation is... (overestimate/underestimate) - Draw a graph to show your thinking
Underestimate
100
Define critical point
A critical point is a point where f'(x) is either 0 or undefined.
100
In this graph is f' (increasing or decreasing) and is f'' (positive or negative)?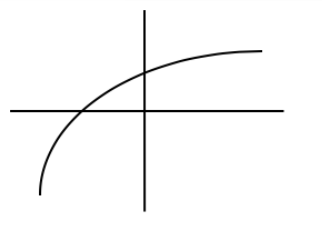
decreasing and negative
200
d/dx[(3x-2x^5)(7x^3+4x^2)]
(3-10x^4)(7x^3+4x^2)+(3x-2x^5)(21x^2+8x)
200
If revenue is given by the function R(p)=1700p-10p2, what price would tickets have to be sold at to maximize revenue?
85
200
If the second derivative is NEGATIVE, the linear approximation is... (overestimate/underestimate) - Draw a graph to show your thinking
Overestimate
200
Find the critical value(s) of the following function:
f(x) = x^3+6x^2+12x
x = -2
200
Estimate where f(x) is concave up given this graph of f(x)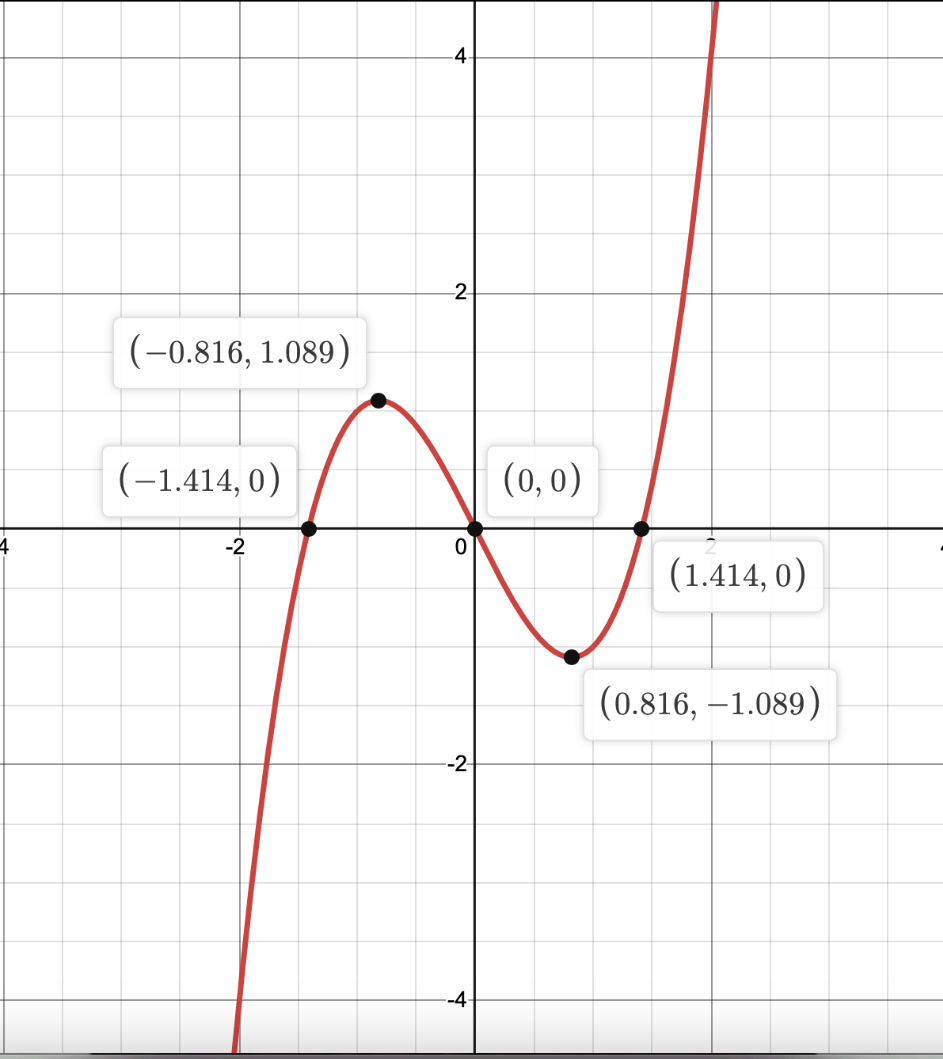
(0, infty)
300
Find the derivative of
f(x)=\frac{x^6-3}{(2x+5)^2}
\frac{6x^5(2x+5)^3-(x^6)(6(2x+5)^2)}{(2x+5)^6}
300
What is the estimated total profit in selling 101 items if P(100) = 10,150 and P'(100) = 89?
otal profit in producing 100 items = 10,150
Approx cost to produce the 101st item = 89
Total cost to produce 101 items = 10,239
300
Ethan's math t-shirt store sells shirts has an initial average cost of $25. Due to the major increase in the love for mathematics, his average cost is increasing by $5 per day. But, because the midterm is coming up, the growth rate of his cost is decreasing.
Express these 3 claims regarding the average cost of Ethan's t-shirts as a function of time!
R(t) = Average t-shirt cost t days from now
R(0) = $25
R'(0) = $5 per day
R' is decreasing, so R''(0) < 0
300
What is an absolute max/min?
This is the max/min of a function on an interval and where the function reaches its maximum/minimum possible value (not just relative)
300
Estimate where f(x) is concave up given this graph of f'(x)
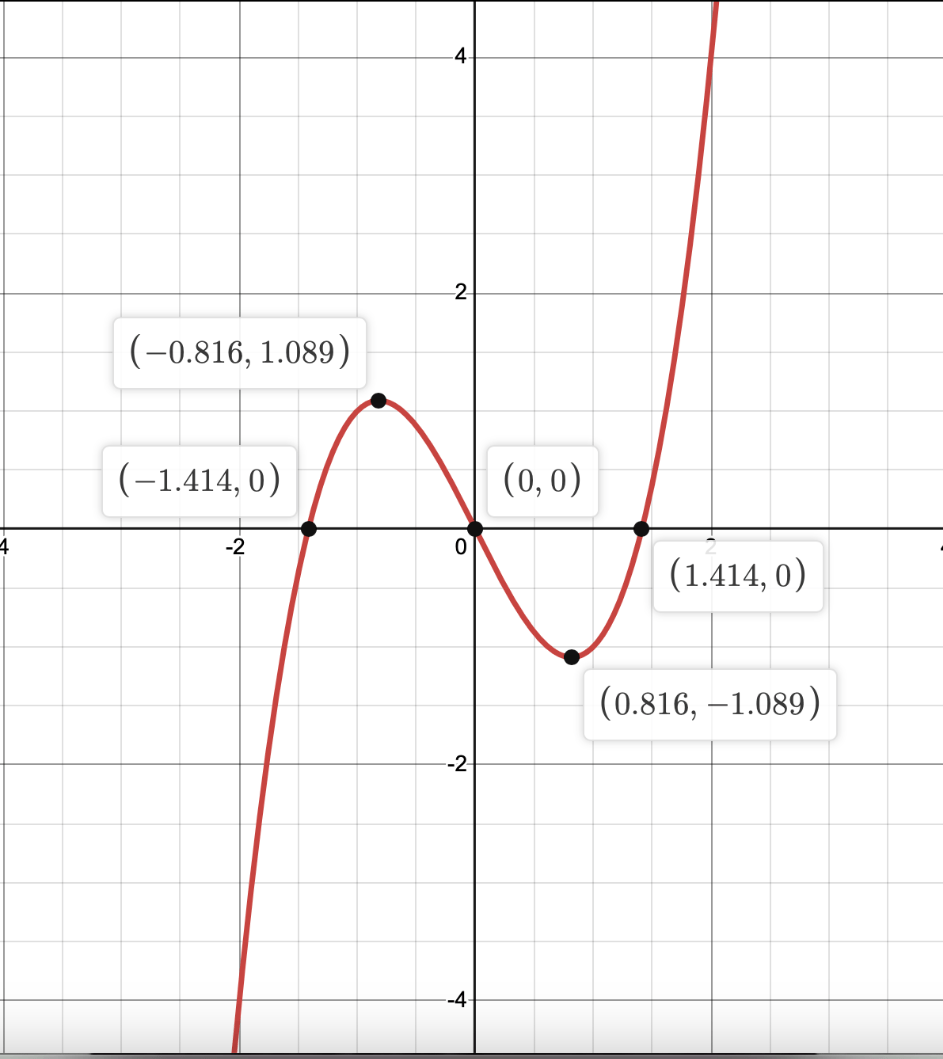
(-infty,-0.816) U(0.816,infty)
400
Find the first and second derivative of
f(x)=(x^2-3)^3
f'(x) = 6x(x^2-3)^2
f''(x)=6(x^2-3)^2+(24x^2(x^2-3))
400
Daily Profit from Ethan's T-shirt shop is $5,000 and is increasing by $20 for each additional t-shirt (unit) sold. Use approximation by increments to estimate the profit when the number of units sold DECREASES by 20
LAF: F(x1) = F(x0) + F'(x0) * (Change in x)
F(x-20) = f(x0) + f'(x0)*(Change in x)
F(x-20) = $5,000 + $20(-20)
F(x-20) = 4600
400
Ethan's math t-shirt store sells shirts has an initial average cost of $25. Due to the major increase in the love for mathematics, his average cost is increasing by $5 per day. But, because the midterm is coming up, the growth rate of his cost is decreasing.
Use Linear Approximation to estimate the the price per t-shirt after 2 weeks
LAF: F(x1) = F(x0) + F'(x0) * (Change in x)
R(14) = R(0) + R'(0) * 14
R(14) = 25 + 5 * 14
R(14) = 95
Remember these are approximates!
400
The first derivative goes from "what" to "what" at a maximum? (Choose from: positive, negative, or zero)
Positive to Negative
400
If they exist, find the critical values, intervals of increasing/decreasing, inflection values, and interval of concavity for the following function
f(x) = x^2-4x
Critical Value: x=2
Inc: (2,inf) Dec: (-inf, 2)
No inflection values. F''(x) is always positive so f(x) is always concave up (-inf,inf)
500
d/dx[(2x^2-8x)^7/(5x^2)]
Jeopardy Labs doesn't like when I try to type long things. Let's do it on the board!
500
At Ethan's T-shirt company, x t-shirts are produced at a price of 1,050 - 5x
Estimate how much additional revenue is earned from increasing the number of units sold from 105 to 106 (Determine the marginal revenue)
R'(105)
R = p * x = (1,050 - 5x) x
R(x) = 1,050x - 5x2
R'(x) = 1,050 - 10x
R'(105) = 0