Adding and Subtract Polynomials
Multiply Polynomials
Factor the polynomials
Applications
Literal Equations
Linear or Quadratic
System of Equations
100
Add the Polynomials
(4x + 9) + (x - 14)
5x - 5
100
3xy*8x
24x^2y
100
x2 - 9
(x+3)(x-3)
100
Find the area of a room that is (3x - 5)ft. by (2x + 1) ft.
6x2 - 7x - 5 ft2
100
Solve the following for x.
- 4y + x = 10
x = 10 + 4y or
x = 4y + 10
100
Which of the following is not considered a linear function?
A. 3x + 2 = y
B. y = 2x + 1
C. y = 3x
D. y = 4x2 - 4
D. It is raised to the second power so it is quadratic.
100
If two lines have the same slope and the same y-intercept, how many solutions does the system have?
A. One solution
B. 2 Solutions
C. No solutions
D. Infinite solutions
Infinite Solutions
200
Add the polynomials and write the answer in standard form.
(-3a - 2) + (7a2 + 5a - 9)
7a2 + 2a - 11
200
Multiply the Polynomials:
9x^2(3x-4)
27x^3-36x^2
200
What is the GCF of the following:
- 3x2 - 3x - 60
-3 or 3
200
What is the perimeter of a rectangle whose side length is (x+2) units and width is (3x-5) units
x+2 + x +2 + 3x - 5 + 3x - 5
8x-6 units
200
Solve the following for x
2x - 3y = 12
(12 + 3y)/2 or 6 + 3/2y
200
What direction does the parabola move?
f(x) = (x-3)^2-5
The parabola moved to the right 3 and down 5.
200
Solve the system of equations.
2x + 3y =16
4x - y = 4
2x + 3y =16
3(4x - y = 4)
14x=28 so x=2
2(2)+3y = 16 so y=4
(2,4)
300
Subtract the polynomials:
(-x2 - 5) - (-3x2 -x -8)
2x2 + x +3
300
Multiply the Polynomials:
3x2 (2x4 + 4)
6x6 + 12x2
300
Factor completely.
2x2 - 11x + 12
(2x - 3)(x - 4)
300
A pumpkin is launched in the air. The equation used to represent the flight is h = -5t2 + 20t + 10, where h is the height of the pumpkin in feet and t is the time in seconds. What is the maximum height the pumpkin will reach during its flight? You may use Desmos.
30 feet
300
Solve the following for r.
C = pir^2
r =sqrt(c/pi)
300
What are the x-intercepts for the following equation.
f(x) = (3x+2)(x-4)
{-2/3, 4}
300
Solve the system of equations.
x + 2y = 4
3x + 6y = 18
No solution. If you graph them they will be parallel.
3(x+2y=4)
3x+6y = 12
3x+6y = 18
400
Subtract the Polynomials:
(k2 + 6k3 -4) - (5k3 + 7k -3k2)
k3 + 4k2 -7k -4
400
(y + 9) (y + 9)
y2 + 18y + 81
400
Find the length and width of a square with an area of
9x2+48x+64
(3x+8)(3x+8)
400
Paul kicks a soccer ball off the ground. The height, h, in feet, of the ball above the ground after t seconds is given by h(t) = -8t2 +32t. How many seconds after the ball is kicked does it hit the ground for the first time? Show how you solved the problem without Desmos.
7 seconds
400
Solve the following for L.
P = 2L + 2W
(P - 2W)/2 = P/2-W
400
Is the following table a linear or quadratic function?
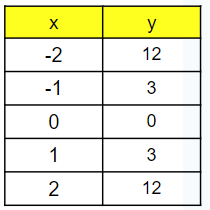Explain how you know.
The second differences are all 6. This means that it is a quadratic equation.
400
Solve the system of equations.
-3x-4y=-2
y=2x-5
-3x-4(2x-5) = -2
-3x-8x+20 = -2
-11x = -22
x =2 y= 2(2)-5 = -1 so (2,-1)
500
Subtract the Polynomials:
(2x2 - 3x) - (x2 -2x + 4)
x2 - x - 4
500
(x - 12)(x + 12)
x2 - 144
500
Factor completely.
32x2+24x-80
8(x + 2)(4x - 5)
500
What are the dimensions of a rectangular prism with a height of 4, a width of (x+3) and a height of (x-2)?
4(x+3)(x-2)
(4x+12)(x-2)
4x2+4x-24
500
Solve for x.
2(4x-3y)=16
x = (8 + 3y)/4 = 2+3/4y
500
Write an equation for the line.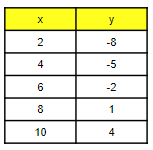
y= 3/2x - 11
500
During a concert, a total of 350 tickets were sold. The tickets were priced at $15 each for general admission and $25 each for VIP seats. If the total revenue from ticket sales was $7600, how many of each type of ticket was sold?
g+v = 350
15g + 25v = 7600
general = 115 tickets
VIP= 235 tickets