Challenge
Given the following information, the lowest 25% of the data is below what value?

7
Given 20 data points, which entry would represent the 20th percentile?
The 5th position
Mean=25
Standard Deviation= 4
Data value=13
Find the z-score for this data value.
-3
If a data point had a z-score of -2.5, would that be considered an unusual value? Why or why not?
Yes, z-scores that are more than 2 standard deviations away from the mean are unusual.
Describe what values are considered outliers using IQR, and what values are considered outliers when using z-scores?
Outliers with IQR: Anything less than Q1-1.5(IQR) or more than Q3+1.5(IQR)
Outliers with z-scores: Anything less than -2 or more than 2.
What is the name of the important parts of a box and whisker plot?
What is 5 number summary
What must be true about data in order for us to find percentiles?
The data must be ordered from low to high.
Which of the following Z-scores would be considered an unusual value:
0, 0.4, -1.3, 2.5, -3.1, 1.7, -3.4, 2.8, 1.2, 1.45
2.5, -3.1, -3.4, and 2.8
The following chart shows goals scored by players in a football season. How many goals would a player have needed to score to be in the top 25% of goal scorers?
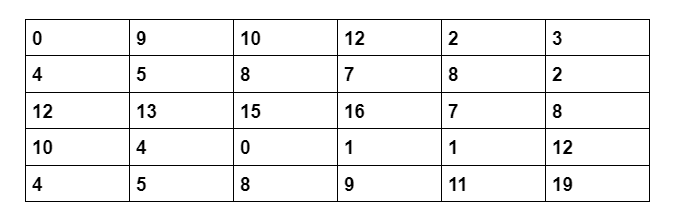
11
Where does Mrs. Beigel's youngest child go to college?
Bentley
Given the following information, what is the high cutoff for an outlier?

32
Using the following data, identify which point would be at the 18th percentile.
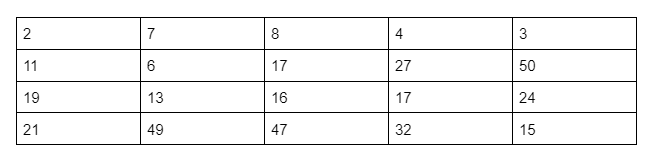
6
The average income of a city was calculated to be $55,000 per person with a standard deviation of $7,500. Find the z-scores for a person making $60,000 and another person making $36,000.
$60K z-score: 0.67
$36K z-score: -2.53
On a physics test, the mean was 50 with a standard deviation of 11.
On a biology test, the mean was 70 with a standard devation of 4.
A student scored a 67 on the physics test and a 73 on the biology test. Which of these scores is better relative to the classes? Explain why.
The score on the physics test is better. Z-score for physics:1.55, z-score for biology: 0.75. The student scored better on physics relative to the class.
The z-scores for 10 students class averages are below (names have no relation to people in class). List which students have a class average that is within 68% of the class.
David: 0.57 Mohammed: -1.2
Ahmed: 2.3 Joe: 0.75
Gabriel: -0.8 Sara: 3.12
Daniel: 1.15 Charles: 0.12
Carl: 0 Stacy: -3.05
David, Joe, Gabriel, Charles, and Carl
Identify any outliers in the following data set.
You must show the IQR, the outlier cutoff boundaries, and the outliers.
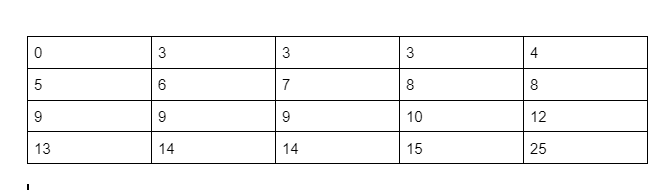
IQR=8
Low Boundary=-7.5
High Boundary=24.5
Outlier= 25
What percentile is the entry 27 at in the following table.

75th percentile
On a statistics test, the mean was 85 with a standard deviation of 3.25. A student has a z-score of 3.1 based on his test result. What was the score this student received on the test?
95.075
What z-scores would be considered outside 99.7% of a data set, regardless of what the data is describing.
Any z-score greater than 3 or less than -3
How many days until Thanksgiving, including today?
23