Stats: Chapter 5 Review

Probability Basics

Probability Rules (5.2)

More Probability Rules (5.2)

Conditional Probability (5.3)

Independence and Tree Diagrams (5.3)

100

Sometimes police use a lie detector test to help determine whether a suspect is telling the truth. It's not foolproof; sometimes it suggests a person is lying when they're not (false positive), and other times it suggests a person is telling the truth when they're not (false negative). For one brand of lie detector, the probability of a false positive is 0.08. Explain what this probability means.

If you take a very large random sample of truthful people and give them a lie detector test, about 8% of the time the test will indicate that the truthful person is lying.

100

Imagine tossing a fair coin 3 times. Give a probability model for this chance process.

The sample space is {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}. Each of the 8 outcomes will be equally likely and have probability

1/8

100

Abigail, Bobby, Carlos, Deanna, and Emily go to the bagel shop for lunch every Thursday. Each time, they randomly pick 2 of the group members to pay for lunch by drawing names from a hat. Find the probability that Carlos or Deanna (or both) ends up paying for lunch on a given Thursday.

7/10 = 0.70 = 70%

100

A random sample of 415 children from England and the U.S. were surveyed to find out which superpower they would most like to have. The data are summarized in the two-way table below.

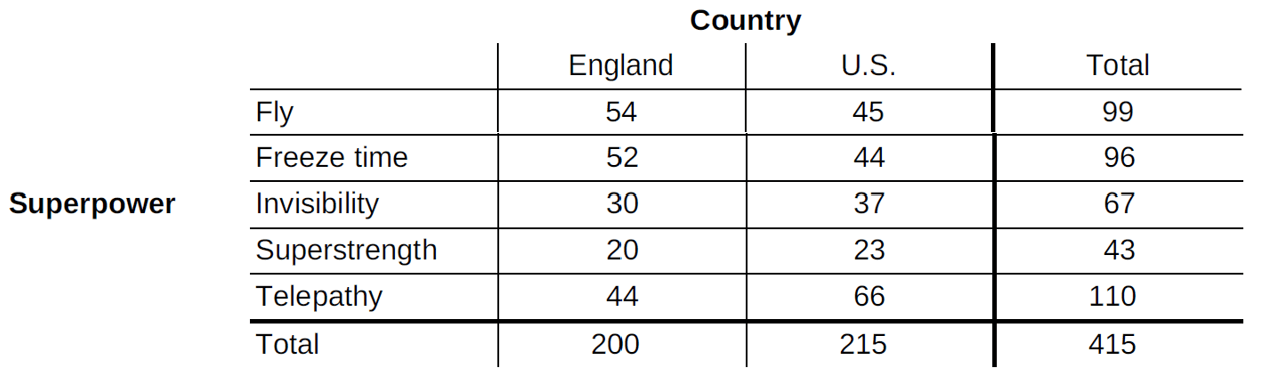
Suppose we select one of these children at random. Define events E: England, T: telepathy, and S: superstrength. Find P(T|E).

P(T|E) = (P(T and E))/(P(E)) = 44/200=0.22

100

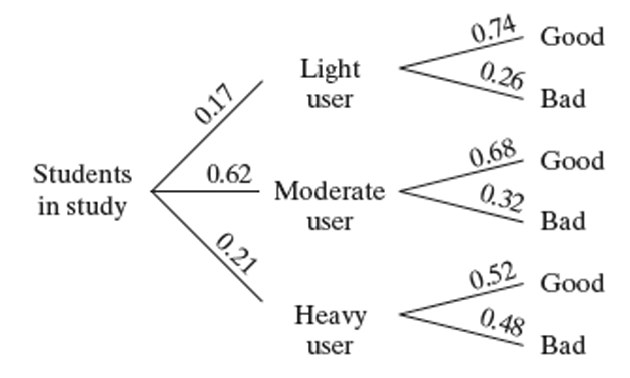
The Kaiser Family Foundation released a study about the influence of social media on young people aged 8-18. In the study, 17% of youth were classified as light social media users, 62% as moderate users, and 21% as heavy users. Of the light users who responded, 74% reported described their grades as good (As and Bs), while only 68% of the moderate users and 52% of the heavy users described their grades as good. Suppose that we select one young person from this study at random. Draw a tree diagram to model this chance process.

200

A very good professional baseball player gets a hit about 35% of the time over an entire season. After the player failed to hit safely in six straight at-bats, a TV commentator said, "He is due for a hit." Explain why the commentator's statement is wrong.

The TV commentator is incorrectly applying the law of large numbers to a small number of at-bats for the player. Chance behavior is unpredictable in the short run, but has a regular and predictable pattern in the long run. The value 35% describes the percent of the time that the player gets a hit in a very long series of trials.

200

Canada has two official languages: English and French. Choose a Canadian at random and ask, "What is your mother tongue?" Here is the distribution of responses, combining many separate languages from the broad Asia/Pacific region:

What is the probability that the chosen Canadian's mother tongue is not English?

P(not English) = 1 - 0.63 = 0.37

200

Choose a young adult (aged 25 to 29) at random. The probability the chosen person did not complete high school is 0.13, they have a high school diploma but no further education is 0.29, and they have at least a bachelor's degree is 0.30. What must be the probability that a randomly selected young adult has some education beyond high school but does not have a bachelor's degree? Explain.

The given probabilities have a sum of 0.72 and the sum of all probabilities should be 1. Thus, the probability that a randomly chosen young adult has some education beyond high school but does not have a bachelor’s degree is 1 – 0.72 = 0.28. There is a 0.28 probability that a young adult has some education beyond high school but does not have a bachelor’s degree.

200

Illegal music downloading is considered by some to be a big problem: 29% of internet users download music files, and 67% of downloaders say they don't care if the music is copyrighted. Find the probability that a randomly selected internet user downloads music and doesn't care if it's copyrighted.

P(downloads music ∩ doesn't care) = (0.29)(0.67) = 0.1943 = 19.43%

200

The figure below shows probabilities for a charity calling potential donors by phone. Each person called is either a recent donor, a past donor, or a prospective donor. At the next stage, the person called either does or does not pledge to donate. Finally, those who make a pledge either do or do not actually make a contribution.

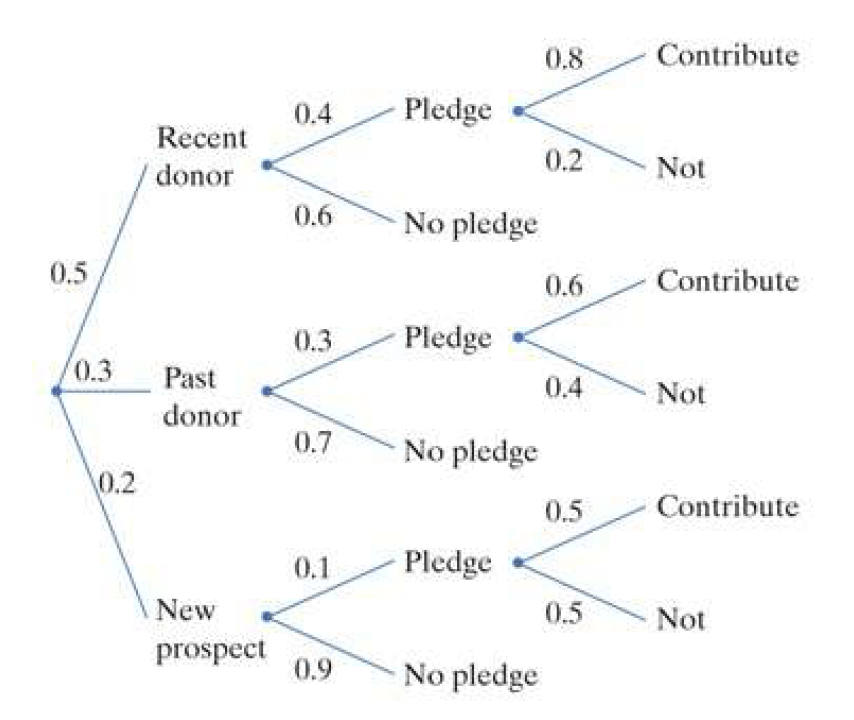
Suppose we randomly select a person who is called. What is the probability that the person contributed to the charity?

P(contributed) = (0.5)(0.4)(0.8)+(0.3)(0.3)(0.6)+(0.2)(0.1)(0.5) = 0.16 + 0.054 + 0.01 = 0.224

300

The figure below shows the results of two different sets of 5,000 fair coin tosses.

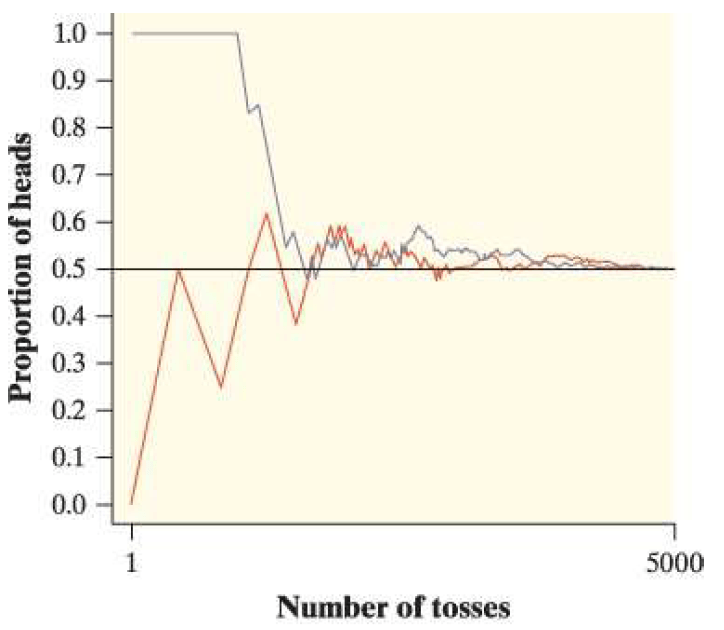
Explain what this graph tells you about chance behavior in the short run and the long run.

In the short run, there was lots of variability in the proportion of heads. In the long run, this proportion became less variable and settled down around 0.50 for both sets of 5,000 tosses.

300

A standard deck of playing cards (no jokers) consists of 52 cards in four suits: clubs, diamonds, hearts, and spades. Each suit has 13 cards, with denominations: ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen, and king. Imagine we shuffle the deck thoroughly and deal one card. Define events F: getting a face card (jack, queen, king) and H: getting a heart. The two-way table summarizes the sample space for this chance process:

Find

P(H^C and F)

P(H^C and F) = 9/52

300

Find

P(H^C or F)

P(H^C or F) = (39+12-9)/52 = 42/52

300

Here is the distribution of the adjusted gross income (in thousands of dollars) reported on individual federal income tax returns in a recent year:

Given that a return shows an income of at least $50,000, what is the conditional probability that the income is at least $100,000?

P(at least $100k|at least $50k)

= (0.100+0.006)/(0.100+0.006+0.215) = (0.106/0.321)~~0.3302

300

The Pew Research Center asked a random sample of over 2,000 adult cell phone users from the U.S. their age and the type of cell phone they own. The two-way table summarizes the data:

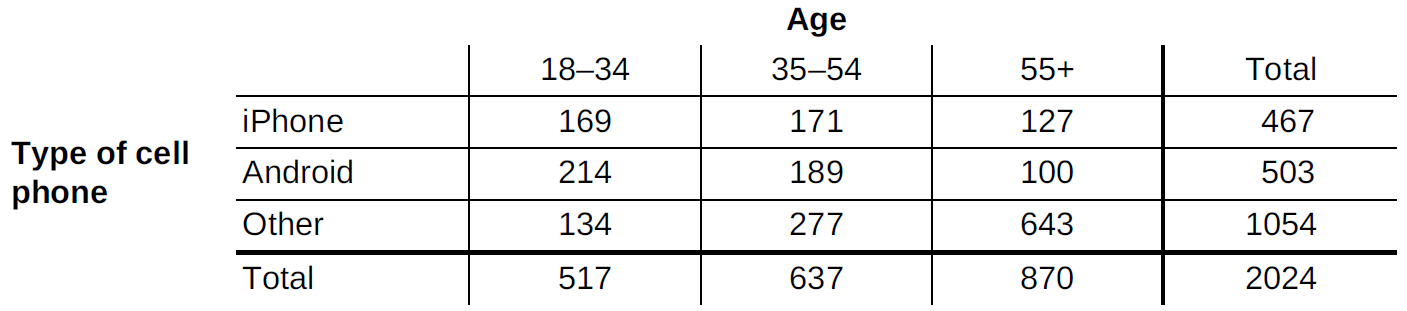
Are the events "iPhone" and "18-34" independent?

If they are independent, then P(iPhone|18-34) = P(iPhone)

169/517 ne 467/2024

0.327 ne 0.231

These events are not independent.

400

A basketball player claims to make 47% of their shots from the field. A simulation of 25 trials where the player took 10 shots were performed. The number of makes in each set of 10 simulated shots was recorded on the dotplot below. What is the approximate probability that the player makes 5 or more shots in 10 attempts?

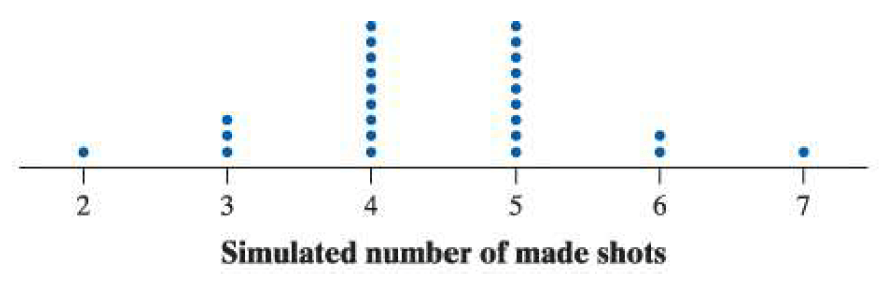
12/25

400

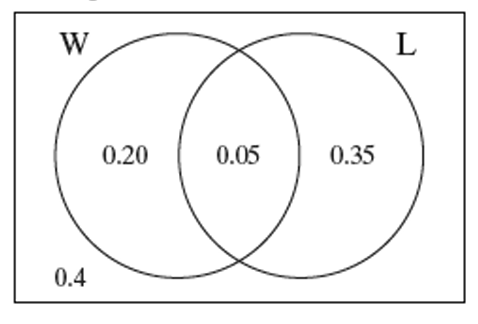
In a large business hotel, 40% of the guests read the Los Angeles Times, 25% of guests read the Wall Street Journal, and 5% of guests read both. Define events L: reads Los Angeles Times, W: reads Wall Street Journal. Make a Venn diagram to display the outcomes of choosing a guest at random.

400

Suppose A and B are two events such that P(A) = 0.3, P(B) = 0.4, and P(A U B) = 0.58. Find

P(A ∩ B)

P(A U B) = P(A) + P(B) - P(A ∩ B)

0.58 = 0.3 + 0.4 - P(A ∩ B)

P(A ∩ B) = 0.12

400

Select an adult at random. Define events D: person has earned a college degree, and T: person's career is teaching. Rank the following probabilities from smallest to largest:

P(D), P(T), P(D|T), P(T|D)

P(T) < P(T|D) < P(D) < P(D|T)

400

Suppose you roll two fair six-sided dice, one red and one green. Are the events "sum is 7" and "green die shows a 4" independent?

Let’s assume that the second die is the green die; there are then six ways for the green die to show a 4: (1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4). Of those, only one adds to 7, so P(sum is 7|green die shows a 4) = 1/6. The events are independent if P(sum is 7) = 1/6. P(sum of 7) = 6/36 = 1/6. These events are independent.

500

Students in a Stats class surveyed an SRS of 100 students at their school to see if they recycled regularly. In the sample, 55 students said they recycle regularly. The dotplot below shows the results of taking 200 SRSs of 100 students from a population in which the true proportion who recycle is 0.50.

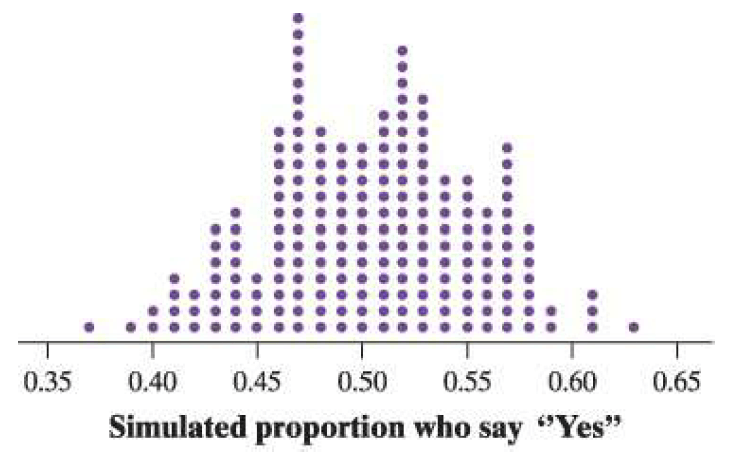
Explain why the sample result (55 out of 100 who said "yes") does not give convincing evidence that more than half of the school's students regularly recycle.

In the simulation, 43 of the 200 samples yielded a sample proportion of at least 0.55. Obtaining a sample proportion of 0.55 or higher is not particularly unusual when 50% of all students recycle.

500

Suppose a student is randomly selected from a large high school. The probability that the student is a senior is 0.22. The probability that the student has a driver's license is 0.30. If the probability that the student is a senior or has a driver's license is 0.36, what is the probability that the student is a senior and has a driver's license?

(0.22+0.30)-0.36=0.16

500

The security system in a house has two units that set off an alarm when motion is detected. Neither one is entirely reliable, but one or both always go off when there is motion anywhere in the house. Suppose that for motion in a certain location, the probability that detector A goes off and detector B does not go off is 0.25, and the probability that detector A does not go off is 0.35. What is the probability that detector B goes off?

P(B goes off) = P(A and B) + P(not A) = (0.65 - 0.25) + 0.35 = 0.40 + 0.35 = 0.75

500

According to Forrest Gump, "Life is like a box of chocolates. You never know what you're gonna get." Suppose a candymaker offers a special "Gump box" with 20 chocolate candies that look alike. In fact, 14 of the candies have soft centers and 6 have hard centers. Suppose you choose 3 candies at random from a Gump box. Find the probability that all three candies have soft centers.

P(all 3 soft) = P(1st soft)*P(2nd soft|1st soft)*P(3rd soft|1st & 2nd soft)

= (14/20)*(13/19)*(12/18)=(2184/6840)~~0.319

500

Suppose you roll two fair six-sided dice, one red and one green. Are the events "sum is 8" and "green die shows a 4" independent?

Let’s assume that the second die is the green die; there are then six ways for the green die to show a 4: (1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4). Of those, only one adds to 8, so P(sum is 8|green die shows a 4) = 1/6. The events are independent if P(sum is 8) = 1/6. P(sum of 8) = 5/36 =/= 1/6. These events are not independent.