Graphing
Substitution
Elimination 1-2
Elimination 3-4
Elimination 5-6
Things to Remember
100
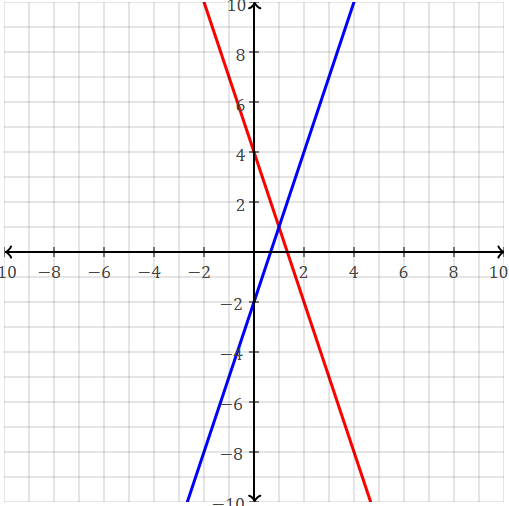
Solve by graphing.
y=3x-2
y=-3x+4
(1,1)
100
Solve by substitution.
y=6x
y=x-5
(-1,-6)
100
Solve using elimination.
-4x-2y=-12
4x+8y=-24
(6, -6)
100
Solve using elimination.
-2x-y=-6
4x+8y=-24
(6, -6)
100
Solve using elimination.
5x+4y=-30
3x-9y=-18
(-6, 0)
100
What does one solution look like?
Intersecting Lines
x = ___
y = ___
200
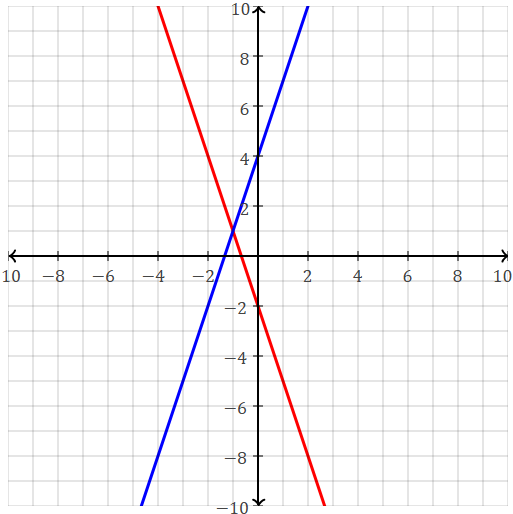
Solve by graphing.
y=3x+4
y=-3x-2
(-1,1)
200
Solve by substitution.
y=7x+17
y=-3x-3
(-2,3)
200
Solve using elimination.
x-y=11
2x+y=19
(10, -1)
200
Solve using elimination.
16x-10y=10
-8x-6y=6
(0, -1)
200
Solve using elimination.
3x-2y=2
-5x+5y=-10
(-2, -4)
200
What does no solutions look like?
Paralell Lines - Not Intersecting
3 = 7
10 = 9
FALSE STATEMENT
300
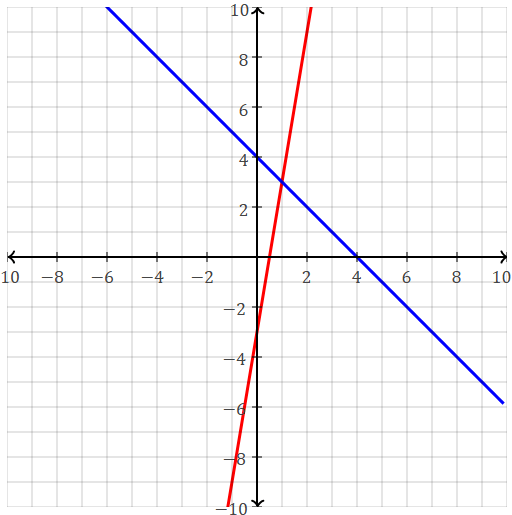
Solve by graphing.
y=-x+4
-6x+y=-3
(1,3)
300
Solve by substitution.
y=0
-x+2y=-7
(7,0)
300
Solve using elimination.
6x-5y=-1
6x+4y=-10
(-1, -1)
300
Solve using elimination.
8x+14y=4
-6x-7y=-10
(4, -2)
300
Solve using elimination.
2x+8y=6
-5x-20y=-15
Infinitely Many Solutions
300
What does infinitely many solutions look like?
Same Line! Always intersecting!
4 = 4
9 = 9
x = x
TRUE STATEMENT
400
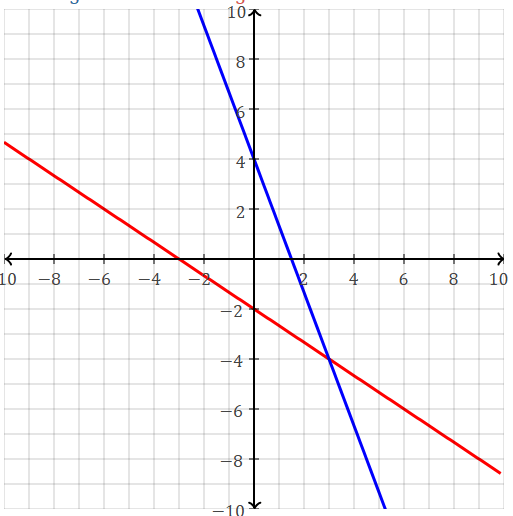
Solve by graphing.
8x+3y=12
2x+3y=-6
(3,-4)
400
Solve by substitution.
y=8x+4
3x-2y=5
(-1,-4)
400
Solve using elimination.
-2x-9y=-25
-4x-9y=-23
(-1, 3)
400
Solve using elimination.
-7x+y=-19
-2x+3y=-19
(2, -5)
400
Solve using elimination.
5x+4y=-14
3x+6y=6
(-6, 4)
400
When writing your answer to a system of equations... what should your answer look like?
An ordered pair!
(x, y)
500
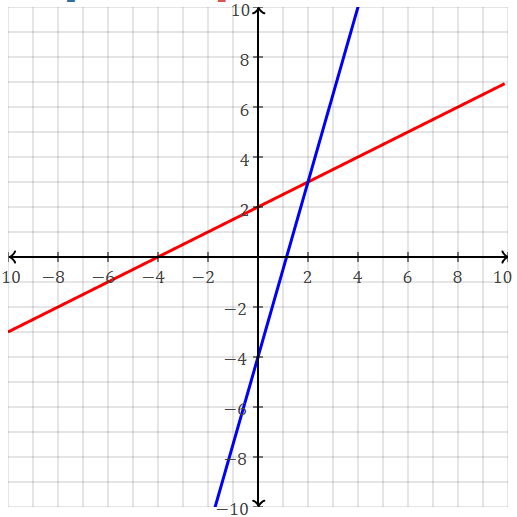
Solve by graphing.
-2y=-7x+8
-4+2y=x
(2,3)
500
Solve by substitution.
5x+y=1
6x-4y=22
(1,-4)
500
Solve using elimination.
8x+14y=4
-12x-14y=-20
(4, -2)
500
Solve using elmination.
-3x+7y=-16
-9x+5y=16
(-4, -4)
500
Solve using elimination.
2x+3y=12
-4x-6y=23
No Solutions
500
You need to have what kind of signs to be able to eliminate variables?
Opposite Signs
One Positive - One Negative