GiRaph
Sub Me IN
Elimination Station
100
What do 2 parallel lines tell you when you graph a system of equations? How does that change if it is a system of inequalities?
In a system of equations, 2 parallel lines means they will have no solutions, whereas with inequalities there is a possibility of solutions depending on the shading.
100
if a=6, use substitution to determine the value of b in the following equation
2a-3b=-15
b=9
100
5x + 2y = 18
–5x + 3y = 2
Use elimination to solve
(2,4)
200
y = 3x + 4
y = –3x + 4
When you graph this system, is it consistent or inconsistent? if consistent, how many solutions does it have? Finally, if it has one solution, label it as a coordinate pair.
consistent
1 solution
(0,4)
200
When should you use substitution to solve a system as opposed to using elimination?
Use your chosen method to solve the following system
x – 3y = 5
2x + y = –18
Substitution can be used most easily when a variable is by itself already and an expression can sub in, but is more adaptable to any situation. Elimination is used when variables are lined up with one another in a system.
(-7,-4)
200
6x + y = 22
2x + 2y = 4
Multiply correctly in order to use elimination to solve.
(4,-2)
300
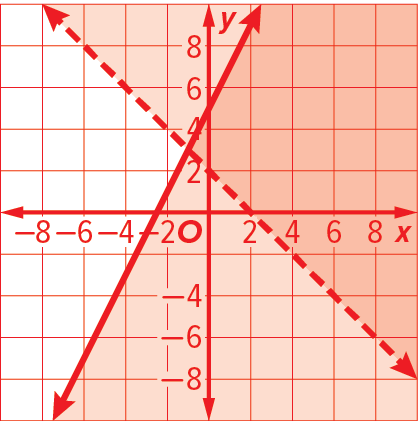
y > –x + 2
y ≤ 2x + 5
Show your solutions to this system in the form of a graph
300
y = 4x – 1
3x + 2y = 20
Find the solution to this system using substitution. Write answer as a coordinate pair.
(2, 7)
300
Antwan is playing a video game where he collects coins and stars worth points. On the first level, he collects 14 coins and 6 stars and earns 4400 points. On the second level, he collects 7 coins and 12 stars and earns 6700 points. Write and solve a system of equations to find how many points a coin and a star are each worth.
14c + 6s = 4400 and 7c + 12s = 6700, where c is the number of points that a coin is worth and s is the number of points that a star is worth
c= 100
s=500