Vocabulary
Graphing
Substitution
Elimination
Random
100
Parallel lines result in what type of solution?
No Solution.
100
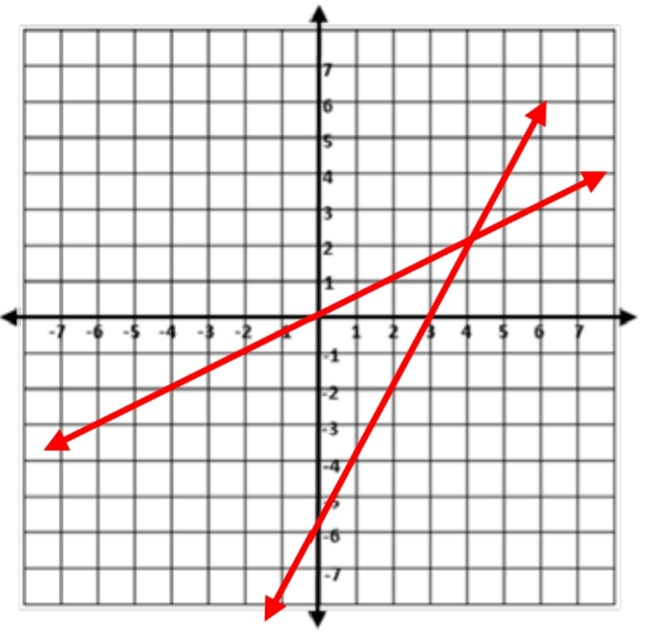
State the solution to the following graph.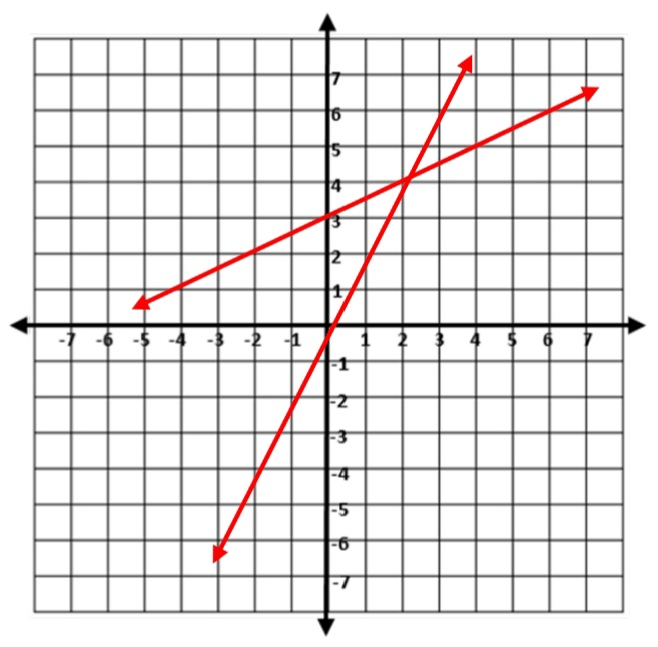
(2,4)
100
Solve the following system by substitution.
y=3x
x+y=-32
(-8,-24)
100
Using elimination solve the following system
-2x+4y=4
3x-4y=2
(6,4)
100
How many solutions does the following system have?
y=1.5x+2
y=3x-1
One.
200
The point of intersection for a system of equations.
Solution to a system of equations.
200
True or False: The solution to this system of equations is (-3,2).
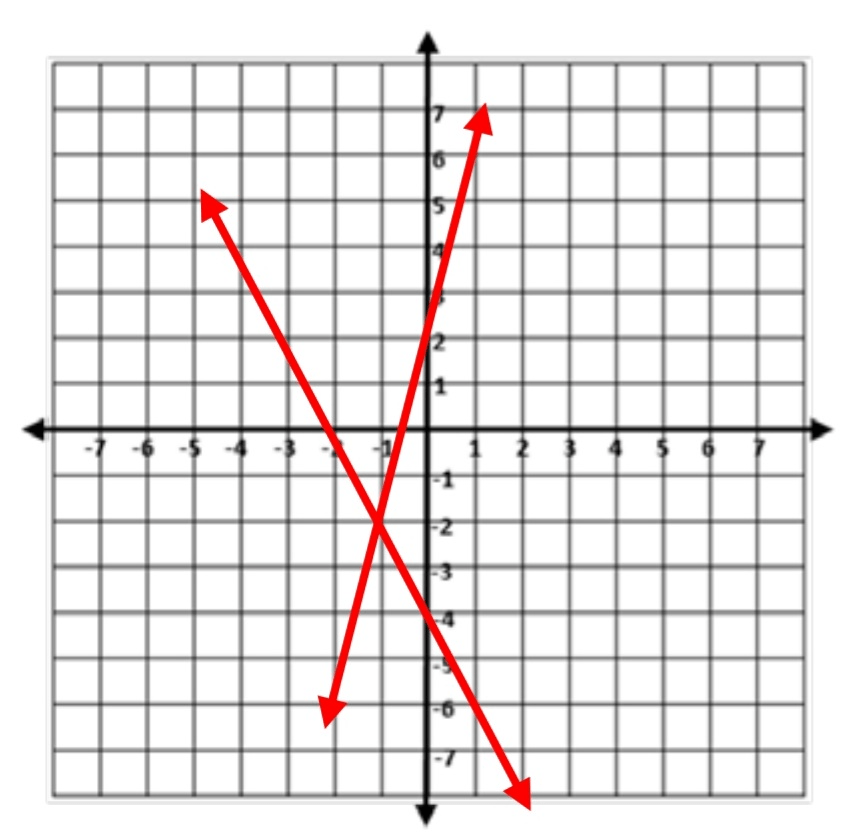
False.
200
Is (2,16) a solution to the following system
y=9x-2
y=3x+10
Yes.
200
Describe what the first step would be in order to solve the following equation by elimination?
-x+2y=-13
2x+3y=12
In situations where neither of the variables in the two equations has opposite coefficients, it may be necessary to multiply one equation by a constant in order to create opposite terms.
200
Identify m and b from the given equation.
y=-3x+6
m= -3
b=6
300
Two or more linear equations that use the same variables.
system of equations
300
State the equations to the following system of equations in slope-intercept form from the given graph.
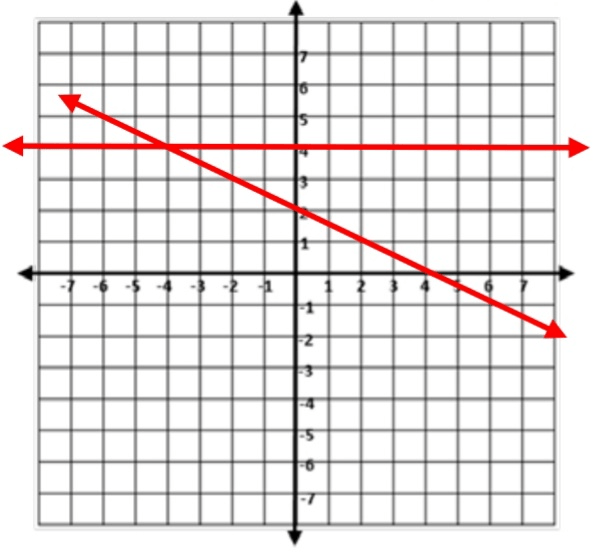
y= -1/2x+3
y=5
300
Solve the following system by substitution.
y=-x+4
5x+6y=13
(11,-7)
300
Is 8x=16 the result of the two equations below added together?
5x-2y=42
-3x+2y=-26
False.
300
Write a second equation that would make this equation a system with "no solution".
y=-8x+15
Any equation with the same slope but diff y-int.
400
When graphing this system of equations the slopes and y-intercepts of the two lines will be the same. What type of solution is this?
Infinitely many solutions.
400
Solve the following system by graphing.
y=x-3
y=2
400
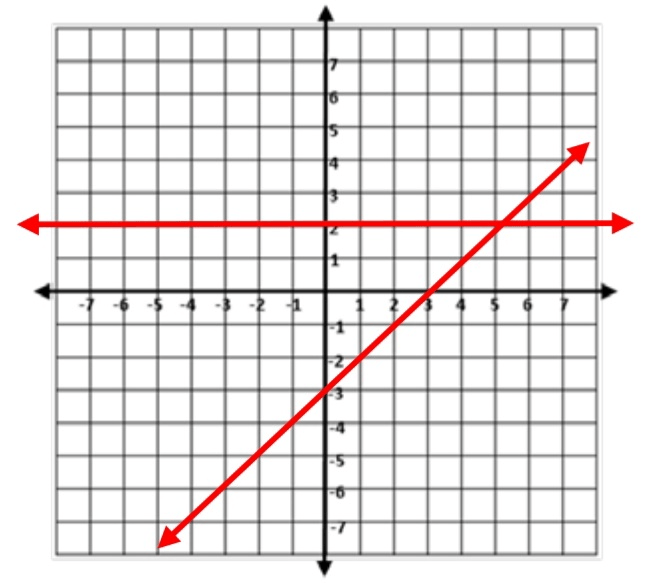
Solve the following system by substitution.
-10x+2y=4
-9x+3y=18
(2,12)
400
Solve the following system by elimination.
-3x+y=-8
4x+3y=28
(4,4)
400
At a bakery, the cost of one cupcake and two slices of pie is $12.40. The cost of two cupcakes and three slices of pie is $20.20. What is the cost of one cupcake?
x+2y=12.40
2x+3y=20.20
$3.20
500
Name the method in which you must first set both equations in slope-intercept form before solving.
Graphing method.
500
Solve the following system of equations by graphing.
y=1/2x
-6x+3y=-18
500
Is (2,1) a solution to the following system?
y=x+2
5x-4y=-3
No.
500
Explain when you think the method of elimination would be most helpful to solve a system of equations rather than one of the previous methods used?
When neither equations are written in slope-intercept form.
500
Create your own real-world system of equations word problem.
Varies.