Systems with Graphs
Solving by Substitution
Solving by Elimination
Mixed
Random
100
What is the solution?
(-1,1)
100
Solve the systems of equations:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations:
14x + 2y = 26
14x + 6y = 50
(1, 6)
100
What strategy would you use?
14x + 2y = 26
-14x - 6y = -50
elimination
100
Determine which method you would use to solve the following system of equations. Explain your reasoning.
6x - 4y = -42
6x + 13y = 9
Elimination - the equations are already in standard form.
200
How many solutions are there?
No Solutions
200
Solve the systems of equations:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve the systems of equations:
-3x - 5y = 2
3x + 5y = 7
No Solution
200
What Strategy would you use?
-5x - 5y = 10
y = -4x -17
Substitution
(-5,3)
200
Is the given point a solution to the system of equations?
Point: (1/2, -2)
6x + 5y = -7
2x - 4y = -8
No
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
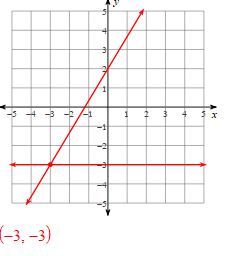
Solve the systems of equations:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations:
6x + 10y = 1
6x + 10y = 1
Infinite Solutions
300
Is there 1 solution, No solution, or Infinite solutions for the following question?
3x - y = 19
-3x + y = 10
No Solutions
300
What is this form called?
y = mx + b
Slope Intercept Form
400
How many solutions are there?
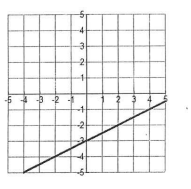
Infinitely Many Solutions
400
Solve the systems of equations:
-8x - 5y = -24
y = 10 + x
(-2, 8)
400
Solve the systems of equations:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
400
How many solutions does the system have?
3y + 4x = 6
12y + 16x = 24
These are the same exact line, therefore they have
Infinite Solutions
400
Is the given point a solution to the system of equations?
Point: (2,6)
x + y = 8
3x - y = 0
Yes
500
Solve the systems of linear equations by graphing:
500
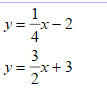
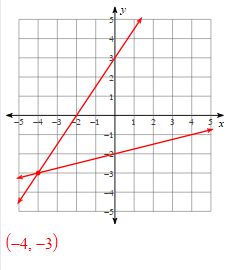
Solve the systems of equations:
y = -7 + 8x
16x - 2y = 14
Infinitely Many Solutions
500
Solve the systems of equations:
-15x + 6y = -36
-8x + 6y = -22
(2, -1)
500
How you tell if the following equations have one, no, or infinite solutions without solving the system?
6x - 14y = 31
6x - 87y = 56
One Solution
If we have different slope (-A/B), then the lines intersect. Therefore, one Solutions
500
What is this form called?
Ax + By = C
Standard Form