Solving by Graphing
Substitution
Solving Equations with Variables on Both Sides
How Many Solutions?
Random
100
What is the solution?
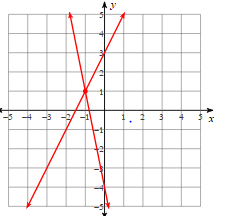
(-1,1)
100
Solve the systems of equations:
-3x + 4y = -2
y = -5
(-6, -5)
100
What should you do with the variables when you have an equation where they're on both sides?
Move all of them to one side.
100
What strategy would be best?
14x + 2y = 26
-14x - 6y = -50
Elimination because the coefficients on x are the same number with opposite signs
100
What is the formula for slope-intercept form?
y = _______
y = mx + b
200
Solve by Graphing
y= 2x + 1
y= -x + 7
(2, 5)
200
Solve the systems of equations:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve for w: 2w + 3 = 4w - 5
w = 4
200
What strategy would be best?
y = 4x + 3
y = -2x + 1
Substitution because both equations are in slope-intercept form
200
In the formula for slope intercept form, what does b represent?
the y-intercept
300
Solve by Graphing:
y = 5/3x + 2
y = -3
300
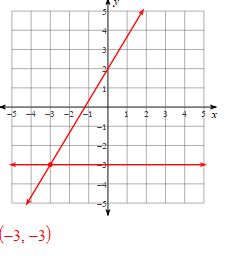
Solve the systems of equations:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve for y: 5(2y + 3) = 6y - (7 - 2y)
y= -11
300
How many solutions?
-6x - 10y = 4
6x + 10y = 0
None
300
What would a system of equations with one solution look like on a graph?
Two lines that intersect at one point.
400
How many solutions are there? (the lines are drawn on top of each other)
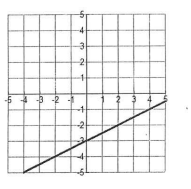
Infinitely Many Solutions
400
Solve the systems of equations:
-8x - 5y = -24
-x + y = 10
(-2, 8)
400
-g + 2(3 + g) = -4(g + 1)
g= -2
400
What strategy would be best?
3x - 4y = 12
2x + 2y = 6
Elimination Method
400
Rise over Run = what?
Slope
500
Solve the systems of linear equations by graphing:
500
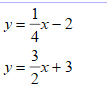
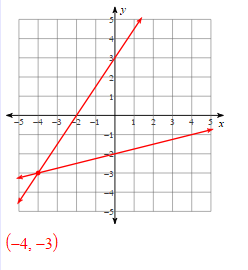
Solve the systems of equations:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
500
1/5(5x - 5) + 3x = -9(1/3x + 4)
x= -5
500
What method would be the best?
3y = 6 - 4x
4y = 3x + 8
Substitution put one of the equations into slope intercept form
500
What would a systems of equations with no solution look like on a graph?
Parallel Lines