x + 3y = 7
8x - 3y = 2
(1,2)
y = 2
x + 2y = 6
(2,2)
y = 2x + 2
y = x - 1
(-3,-4)
What are 3 methods of solving systems of equations?
Graphing, Elimination, and Substitution
When graphing linear inequalities what kind of line does < and > represent?
Dashed/Dotted Line
4x - 3y = 16
5x + 3y = 20
(4,0)
y = 3x
2x + y = 10
(2,6)
y = 2x + 5
y = x + 3
(-2,1)
y = 2x + 3
y = 2x - 5
Lines with the same slope have how many solutions?
No solution
When graphing linear inequalities what does ≤ and ≥ mean in terms of the lines?
Use a Solid Line
-2x - 9y = -25
-4x - 9y= 23
(-1,3)
-5x+y = - 1
2y = 3x + 12
(2,9)
3x - 2y = 8
x + y = 6
(4,2)
2x - 3x = 10
6x + 4x = -20
Would the grouping, substitution, or elimination method be the most efficient and why?
Elimination Method, because the equations are already in standard form.
y>3x+2
y<x-2
Would the point (-4,-8) be a solution? Why?
Yes, because -8>3(-4)+2 and -8<-4-2.
4x - 9y = 2
12x - 5y = -38
(-4,-2)
2x - 3y = -2
4x+y= 24
(5,4)
y = 1/2x + 2
y = 1/4x + 4
(8,6)
y = -5x + 3
2y + 10x = 6
Would the grouping, substitution, or elimination method be the most efficient and why?
Substitution Method, because the y variable is already isolated.
y>-2x
y<1/2x-4
Is the point (2,-6) a solution? Why?
No, because -6 is not > -2(2).
At a school concert, Alison collected $48 for 5 adult tickets and 2 student tickets. Jared collected $32 for 3 adult tickets and 2 student tickets. If x represents the cost for each adult ticket and y represents the cost for each student ticket, what is the cost for each adult and student ticket?
Adult: $8/ticket
Student: $4/ticket
x + y = 10
-y = 5 + x
No solution
4x - 5y = 15
8x + 5y = 45
(5,1)
The method of solving equations is where you add or subtract equations to end up with one variable.
Elimination Method
What is the system of inequalities that would represent this graph?
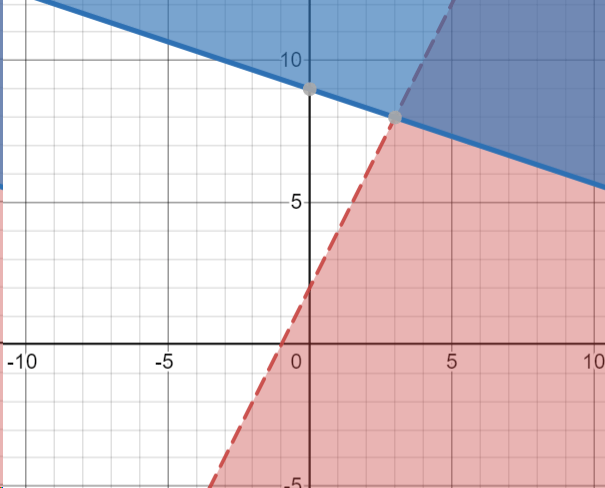
y>=-1/3x+9
y<2x+2