Elimination
Substitution
Graphing
Vocabulary
Systems of Inequalities
100
x + 3y = 7
8x - 3y = 2
(1,2)
100
y = 2
x + 2y = 6
(2,2)
100
y = 2x + 2
y = x - 1
(3,-4)
100
what are 3 methods of solving systems of equations?
elimination
graphing
substitution
100
What kind of line do you use when graphing linear inequalities with these symbols: < and >
dashed
200
4x - 3y = 16
5x + 3y = 20
(4,0)
200
y = 3x
2x + y = 10
(2,6)
200
y = 2x + 5
y = x + 3
(-2,1)
200
y = 2x + 3
y = 2x - 5
Lines with the same slope have:
A) one solution
B) no solution
C) infinite solutions
B
200
What kind of line do you use when graphing linear inequalities with these symbols: ≤ and ≥
solid line
300
-2x - 9y = -25
-4x - 9y= 23
(-1,3)
300
y = 5x - 1
2y = 3x + 12
(2,9)
300
3x - 2y = 8
x + y = 6
(4,2)
300
How can you tell if a linear system has infinitely many solutions?
The equations are the same, and the lines lie on top of each other
300
Systems of inequalities can only be solved ______.
Graphically
400
4x - 9y = 2
12x - 5y = -38
(-4,-2)
400
2x - 3y = -2
y= -4x + 24
(5,4)
400
y = 1/2x + 2
y = 1/4x + 4
(8,6)
400
How many solutions does this system have:
y = -5x + 3
2y + 10x = 6
A) one solution
B) no solution
C) infinite solutions
C
400
How is graphing systems of inequalities different than graphing systems of equations?
They use dashed lines sometimes, and you have to shade to find the solution
500
The equations 5x + 2y = 48 and 3x + 2y = 32 represent the money collected from school concert tickets sales during two class periods. If x represents the cost for each adult ticket and y represents the cost for each student ticket, what is the cost for each adult ticket?
x=8
500
x + y = 10
-y = 5 + x
no solution
500
4x - 5y = 15
8x + 5y = 45
(5,1)
500
The method of solving equations where you add or subtract equations to end up with one variable.
Elimination
500
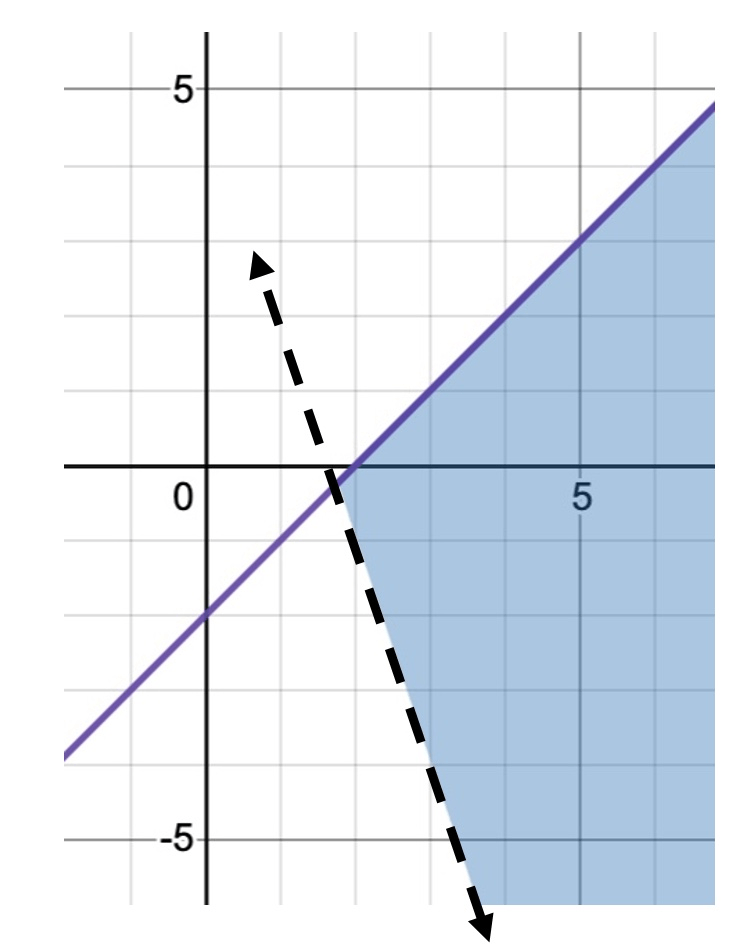
Graph the system of linear inequalities. ONLY SHADE THE SOLUTION!
y ≤ x − 2
y > −3x + 5
