elimination
substitution
graphing
vocabulary
systems of inequalities
100
x + 3 y = 5
2x - 3y = -8
(-1,2)
100
y = 2
3x + 2y = 10
(2,2)
100
y = 2x + 2
y = x - 1
(3,-4)
100
what are the 3 methods of solving systems of equations
elimination
graphing
substitution
100
when graphing linear inequalities what does < and > mean
Use a Dotted Line
200
4x - 3y = 16
5x + 3y = 20
(4,0)
200
y = x + 1
2x + y =10
(3,4)
200
y = 2x + 5
y = x + 3
(-2,1)
200
there are two graphs on the same coordinate plane
systems of equations
200
what does ≤ and ≥ mean when graphing linear inequalities
solid line
300
-2x - 9y = -25
-4x - 9y= 23
(-1,3)
300
y = 5x - 1
2y = 3x + 12
(2,9)
300
3x - 2y = 8
x + y = 6
(4,2)
300
How can you tell if a linear system has infinitely many solutions?
the equations are the same and the lines lie on top of each other
300
systems of inequalities can only be solved ______
graphically
400
4x - 9y = 2
12x - 5y = -38
(-4,-2)
400
2x - 3y = -2
y= -4x + 24
(5,4)
400
y = 1/2x + 2
y = 1/4x + 4
(8,6)
400
what does it mean when the lines are parallel or they have the same slope and different y-intercepts or when you solve the equations and get a false statement with no variables remaining.
no solution
400
How is graphing systems of inequalities different than graphing systems of equations?
they use dotted lines sometimes and you have to shade to find the solution
500
The equations 5x + 2y = 48 and 3x + 2y = 32 represent the money collected from school concert tickets sales during two class periods. If x represents the cost for each adult ticket and y represents the cost for each student ticket, what is the cost for each adult ticket?
x=8
500
x + y = 10
-y = 5 + x
no solution
500
4x - 5y = 15
8x + 5y = 45
(5,1)
500
The method of solving equations where you add or subtract equations to end up with one variable.
elimination
500
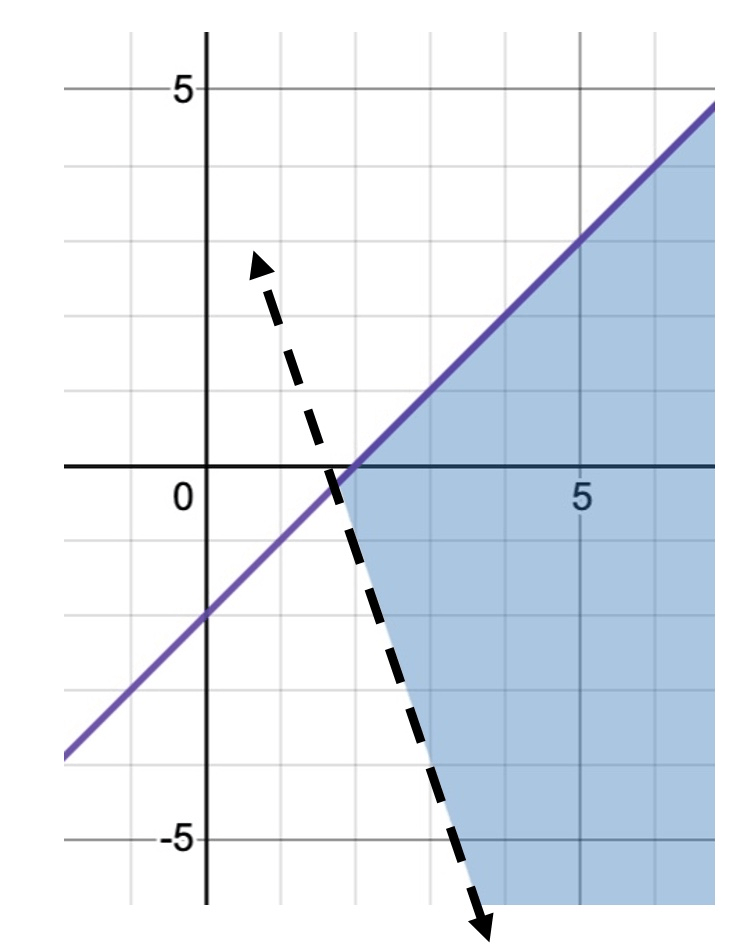
y ≤ x − 2
y > −3x + 5
