Systems of Equations Test Review

Elimination

400

Solve the systems of equations using Elimination:

4x + 8y = 20

4x - 2y = 30

4x + 8y = 20               Substitute y into an equation

-4x + 2y = -30  +            4x + 8(-1) = 20            

      10y = -10                     4x - 8 = 20                  

        y = -1                              4x = 28                 

Solution:  (7 , -1)                     x = 7                   

500

Solve the systems of equations using Elimination:

6x - 5y = -1

-3x - 2y = 5

6x - 5y = -1                Substitute y into an equation

-6x - 4y = 10  +              6x - 5(-1) = -1             

      -9y = 9                        6x + 5 = -1                 

        y = -1                               6x = -6                

Solution:  (-1 , -1)                       x = -1               

Substitution

400

Solve the systems of equations using substitution:

x = 2y - 11

x + 2y = 13

2y - 11 + 2y = 13      Substitute y into an equation

         4y - 11 = 13              x = 2(6) - 11           

                4y = 24                 x = 12 - 11             

                 y = 6                    x = 1                     

                                   Solution:  (1 , 6)  

500

Solve the systems of equations using substitution:

x = -3y + 1

x = 5 - y

-3y + 1 = 5 - y          Substitute y into an equation

 -2y + 1 = 5                         x = -3(-2) + 1           

       -2y = 4                           x = 6 + 1                

          y =  -2                         x = 7                     

                                  Solution:  (7 , -2)          

Graphing

400

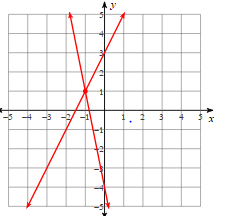
Solve the system of equations graphically.

y = 2x + 3

2y = -10x - 8

(-1,1)

500

Solve the system of equations graphically.

y - 2x = 4

x = y - 1

Solution:  (-3,-2)

One/No/Infinite Solutions

400

State and prove whether the following system of equations has one solution, no solutions, or infinite solutions.

14x - 6y = 10

-7x + 3y = -5

14x - 6y = 10

-14x + 6y = -10  +

0 = 0

Infinite Solutions!

500

State and prove whether the following system of equations has one solution, no solutions, or infinite solutions.

-3x + 3y = 4

-x + y = 3

-3x + 3y = 4

3x - 3y = -9  +

0 = -5

No Solutions!

950

State and prove whether the following system of equations has one solution, no solutions, or infinite solutions.

y = 2x - 4

y = -x + 5

2x - 4 = -x + 5                                                     

3x - 4 = 5              Substitute x into an equation     

3x = 9                                y = 2(3) - 4                

x = 3                                  y = 6 - 4                     

One Solution:  (3 , 2)         y = 2                         

Word Problems

400

Write let statements, set up a system of equations, and solve:

The sum of two numbers is 33.  The difference of the two numbers is 11.  Find the numbers.

Let x = a number

y = another number

x + y = 33                  Substitute x into an equation

x - y = 11   +                     22 + y = 33                

2x = 44                                   y = 11                   

x = 22                     Solution: (22 , 11)                

500

Write let statements, set up a system of equations, and solve:

At a restaurant, the total price for 6 wings and 1 pizza is $16.  The total for 18 wings and 2 pizzas is $39.50.  What is the price of a pizza?

Let x = $ for wings

y = $ for pizza

6x + 1y = 16   <-- * by (-3)                                  

18x + 2y = 39.50                                                  

-18x - 3y = -48  +                                                

-1y = -8.5                                                             

y = 8.5                It costs $8.50 per pizza