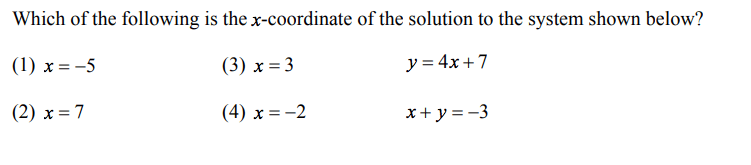
x = -2
Determine the values of x that satisfies the quadratic-linear system shown below:
x = {1, 4}
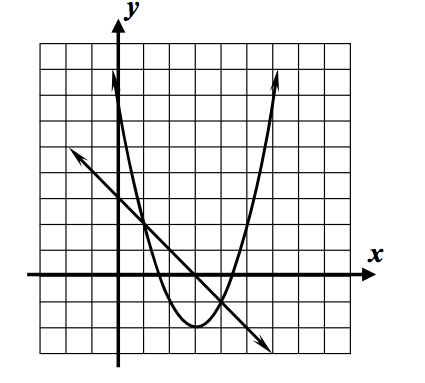
List one point that lies in the solution set of the system of inequalities graphed below?
Answers will vary
Cedric and Zelda went shopping at Price Buster.
Cedric bought 2 jumbo rolls of aluminum foil and 3 packages of AA batteries for a total cost of $21.
Zelda bought 5 identical jumbo rolls of aluminum foil and 2 identical packages of AA batteries for a total cost of $25.
Write a system of equations representing the scenario.
Let a= aluminum foil
Let b= batteries
2a + 3b = 21
5a + 2b = 25
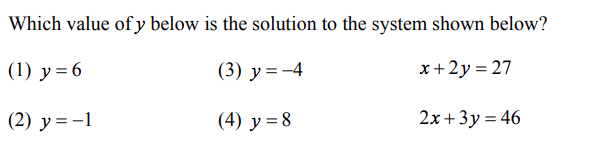
y = 8
On your graphing board.
Graph: y = x +7
y= 11- x
to determine the solution of this linear system.
(2, 9)
Determine if the point (0,4) is a solution to the
system of inequalities graphed below. Justify your
answer.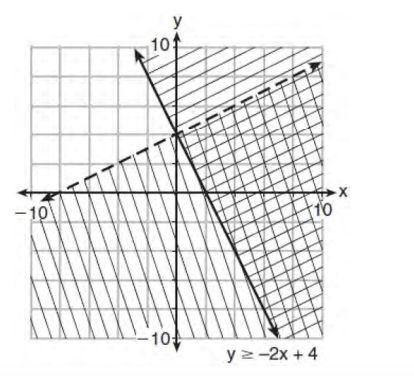
No because it falls on a dashed line so it does not satisfy both inequalities.
Franco and Caryl went to a bakery to buy desserts. Franco bought 3 packages of cupcakes and 2 packages of brownies for $19. Caryl bought 2 packages of cupcakes and 4 packages of brownies for $24. Let x equal the price of one package of cupcakes and y equal the price of one package of brownies.
a) Write a system of equations that describes the given situation.
b) Determine the exact cost of one package of cupcakes.
a) 3x + 2y = 19
2x + 4y = 24
b) $3.50
Use the substitution method to determine the solution to the system shown below. (You need to find both a and b)
2a + 3b = 12
a = 0.5b − 6
a = -3, b = 6
Let f(x) = −2x2 and g(x) = 2x − 4.
Graph f(x) and g(x) on your whiteboard.
Determine the values of x that satisfy f(x) = g(x).
x = {-2, 1}
On the graphing side of your whiteboard,
Graph:
y ≥ 4x + 2
2x + 3y < -3
Label the solution set S.
on graph
A drama club is selling tickets to the spring musical. The auditorium holds 200 people. Tickets cost $12 at the door and $8.50 if purchased in advance. The drama club has a goal of selling at least $1000 worth of tickets to Saturday’s show.
a)Write a system of inequalities that can be used to model this scenario.
b) If 50 tickets are sold in advance, what is the minimum number of tickets that must be sold at the door so that the club meets its goal? Justify your answer.
a) x + y is less than or equal to 200
12x + 8.50y is greater than or equal to 1000.
b) At least 48