Methods
Graphing
Substitution
Elimination
Parallel and Perpendicular
100
What are the three practiced methods used for solving systems of equations?
Graphing Method, Substitution Method, and Elimination Method.
100
What does a system of linear equations, with no solution, look like?
Two Parallel Lines
100
To use the substitution method, what is the first step that needs to happen?
Solve one of the equations for a single variable (either variable will work)
100
What is the goal when using the Elimination Method?
To "eliminate" at least one of the variables when adding the equations together.
100
Find the slope of a line parallel to:
y=-5/2x-3
-5/2
200
Which method would be the fastest when solving this system of linear equations?
4x-3y=-2
2x-3y=6
The Elimination Method
200
What does a system of linear equations, with one solution, look like?
Two different lines with one intersection (aka two lines touching once)
200
Once one of the equations is solved for a single variable, what do you do with that solved equation?
Plug it in to the unsolved equation for the variable we solved for.
200
What would you do first to set up for elimination:
3x+8y=14
-6x+4y=-8
Multiply the top equation by 2
OR
Multiply the bottom equation by -2
200
Find the slope of a line perpendicular to:
y=-5/4x
4/5
300
Which method would be fastest to solve this system of linear equations?
y=-2x+3
y=-x
The Substitution Method
300
What does a system of linear equations, with infinitely many solutions, look like when graphed?
The same line twice (one on top of the other)
300
The solution of the following system of equations:
y=7x-11
y=6x-9
(2,3)
Show your work.
300
The solution of the following system of equations:
9x+8y=-25
-9x-8y=27
No Solution.
Show your work.
300
How do you know two equations are parallel?
They have the same slope and different y-intercepts.
400
In what method do you replace a variable with something of equal value?
The Substitution Method
400
What is the solution to this system of equations?
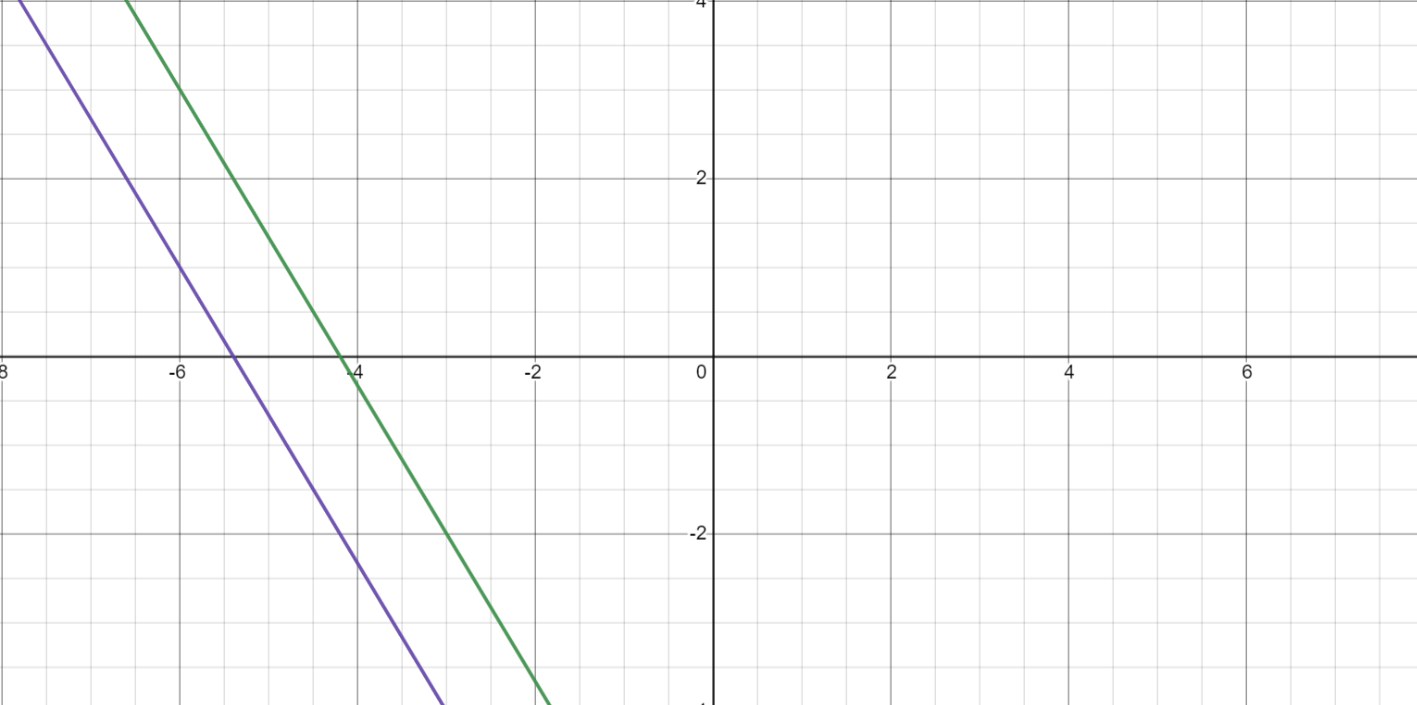
No Solution.
400
The solution of the following system of equations:
y=x+5
-3x+3y=-3
No Solution
Show your work.
400
The solution of the following system of equations:
-8x-3y=14
16x+5y=-26
(-1, -2)
Show your work.
400
How can you tell that two equations are perpendicular?
They have slopes that are opposites and reciprocals of each other.
500
What method are you using when you attempt to have one variable with the same number but opposite signs in a system?
The Elimination Method
500
What is the solution to this system of equations?
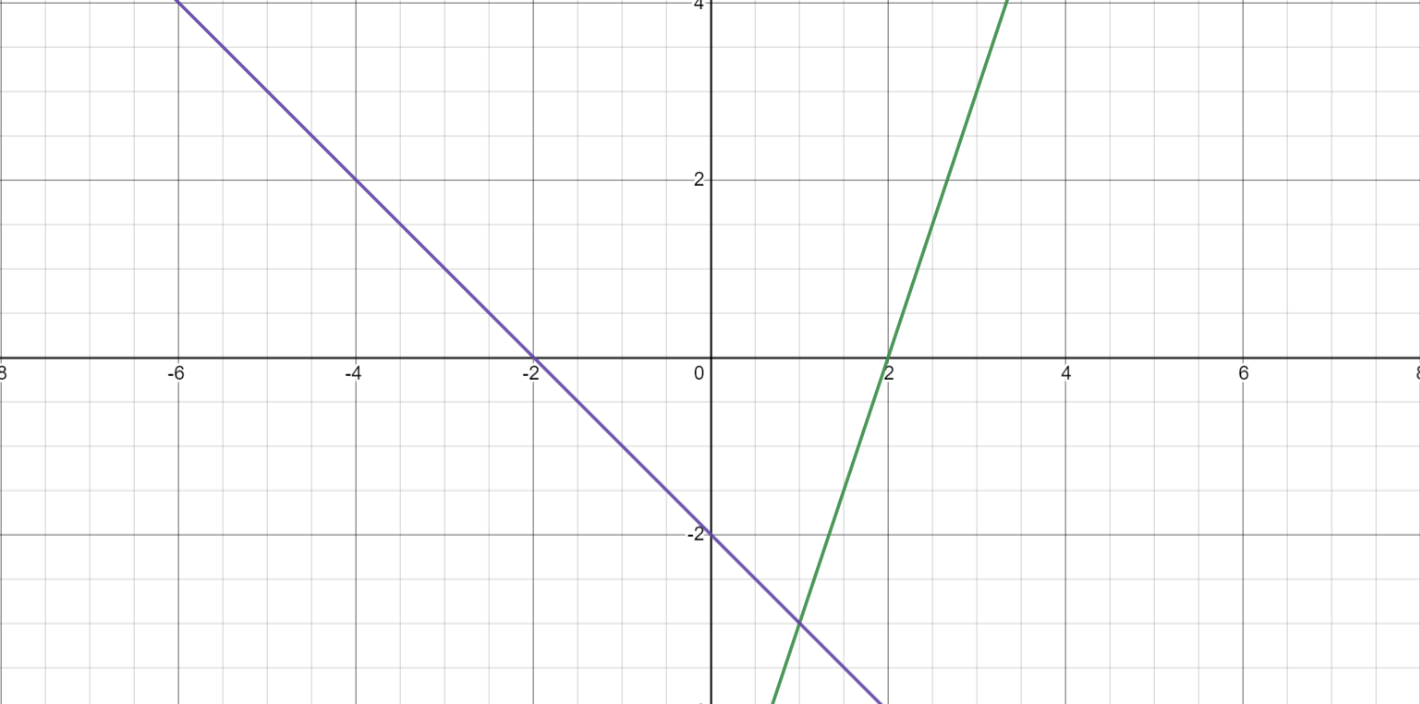
(1, -3)
500
The solution of the following system of equations:
x-7y=-3
2x-2y=6
(4, 1)
Show your work.
500
The solution of the following system of equations:
4x+6y=14
-3x+4y=15
(-1, 3)
Show your work.
500
How can you tell if two lines are perpendicular on a graph? (What is the definition of perpendicular?)
They meet at a 90 degree angle.