Solve by Graphing
Call for Subs
ELIMINATE!
Systems Trivia
Words, Words, Words
100
What is the solution?
(-1,1)
100
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
100
Is the given point a solution to the system of equations?
Point: (2,6)
x + y = 8
3x - y = 0
Yes
100
The difference of two numbers is 12. Their sum is 54. Find the smaller of the two numbers
21
(Other number is 33)
200
How many solutions are there?
No Solutions
200
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve the systems of equations using Elimination:
-3x - 5y = 2
3x + 5y = 7
No Solution
200
Is the given point a solution to the system of equations?
Point: (1/2, -2)
6x + 5y = -7
2x - 4y = -8
No
200
There are two numbers, the sum is 22. The larger number is one more than twice the smaller number. What are the two numbers?
7 and 15
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
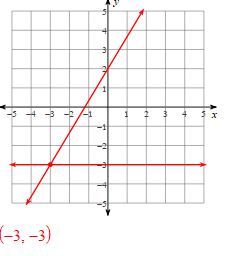
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations using Elimination:
-6x - 10y = 4
-3x - 5y = 7
No Solution
300
What is true of lines with no solution?
They are parallel
-or-
They have the same slope, but different intercepts
300
There are 13 animals in the barn. Some are chickens and some are pigs. There are 40 legs in all. How many of each animal are there?
chickens: 7
pigs: 6
400
How many solutions are there?
Infinitely Many Solutions
400
Solve the systems of equations using substitution:
-8x - 5y = -24
-x + y = 10
(-2, 8)
400
Solve the systems of equations using Elimination:
x + 8y = 22
3x + 4y = -14
(-10, 4)
400
What would you multiply the top equation by if you wanted to eliminate the "x" terms:
0.3x - 0.2y = -2.1
0.6x + 1.3y = 0.9
-2
400
A jar contains nickel and dimes valued at $1.70. There are 21 coins in the jar. How many of each coin is there?
13 dimes and 8 nickels
500
Solve the systems of linear equations by graphing:
500
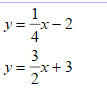
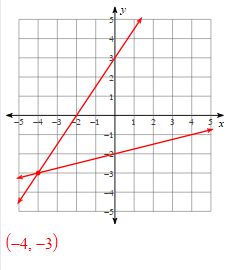
Solve the systems of equations using substitution:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
500
Solve the systems of equations using Elimination:
-5x + 2y = -12
4x - 3y = 11
(2, -1)
500
What does it mean if a system of equations was "dependent"?
The lines are equal.
500
The high school marching band and a Spanish club are planning trips to Europe. In the marching band, 35 students and 4 adults cost a total of $135,400. In the Spanish club, 11 students and 2 adults cost $45,600. If the students and adults cost the same, how much does a student cost?
student cost: $3,400