Solve by Graphing
Solve by Substitution
Solve by Elimination
Suprise
100
What is the solution?
(-1,1)
100
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
100
What strategy would you use?
14x + 2y = 26
-14x - 6y = -50
elimination
200
How many solutions are there?
No Solutions
200
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve the systems of equations using Elimination:
-4x - y = 6
-x + 2y = -12
(0, -6)
200
What strategy would you use?
-5x - 5y = 10
y = -4x -17
substitution
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
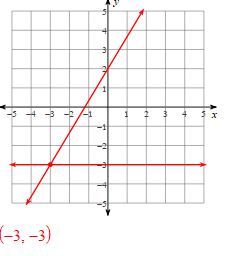
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations using Elimination:
-2x + 10y = 6
-x - y = -9
(7,2)
300
Is there 1 solution, No solution, or Infinite solutions for the system of linear equations below?
3x - y = 19
-3x + y = 10
No Solutions
400
How many solutions are there?
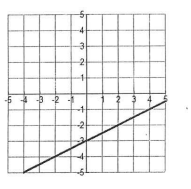
Infinitely Many Solutions
400
Solve the systems of equations using substitution:
-8x - 5y = -24
-x + y = 10
(-2, 8)
400
Solve the systems of equations using Elimination:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
400
The senior classes at High School A and High School B planned separate trips to New York City. The senior class at High School A rented and filled 1 van and 6 buses with 372 students. High School B rented and filled 4 vans and 12 buses with 780 students. Each van and each bus carried the same number of students. How many students can a van carry? How many students can a bus carry?
Van: 18, Bus: 59
500
Solve the systems of linear equations by graphing:
500
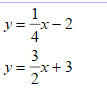
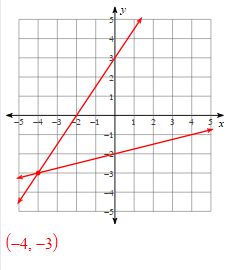
Solve the systems of equations using substitution:
y = 8x + 13
-5x + 4y = -2
(-2, -3)
500
Solve the systems of equations using Elimination:
-15x + 6y = -36
8x - 6y = 22
(2, -1)