Solve by Graphing
Solve by Substitution
Solve by Elimination
Linear Inequalities
Miscellaneous
100
What is the solution?
(-1,1)
100
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
100
< and > indicate that you should draw what kind of line?
Dotted
100
Is the given point a solution to the system of equations?
Point: (2,6)
x + y = 8
3x - y = 0
Yes
200
How many solutions are there?
No Solutions
200
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve the systems of equations using Elimination:
-3x - 5y = 2
3x + 5y = 7
No Solution
200
Greater than and greater than or equal to symbol mean you shade _______ your inequality
above
200
Is the given point a solution to the system of equations?
Point: (1/2, -2)
6x + 5y = -7
2x - 4y = -8
No
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
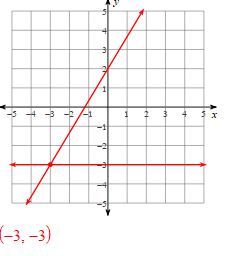
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = 0
No Solution
300
What is the rule that we have to remember when multiplying or dividing by a negative number with inequalities?
You have to flip the sign
300
What would you multiply the top equation by if you wanted to eliminate the "x" terms:
0.3x - 0.2y = -2.1
0.6x + 1.3y = 0.9
-2
400
How many solutions are there?
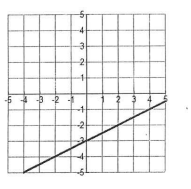
Infinitely Many Solutions
400
Solve the systems of equations using substitution:
-8x - 5y = -24
-x + y = 10
(-2, 8)
400
Solve the systems of equations using Elimination:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
400
Is the graph of the systems of equations correct?
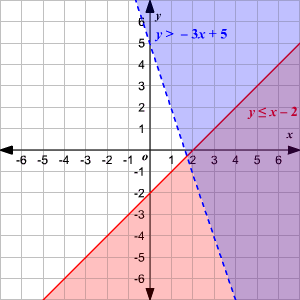
Yes
400
True/False: A matrix that has a 1 0 # on the top of the matrix and 0 1 # on the bottom results in a coordinate answer (x,y)
True
500
Solve the systems of linear equations by graphing:
500
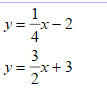
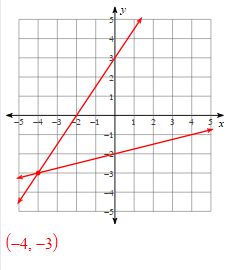
Solve the systems of equations using substitution:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
500
Solve the systems of equations using Elimination:
-15x + 6y = -36
8x - 6y = 22
(2, -1)
500
Give a solution to the system of inequalities graphed below: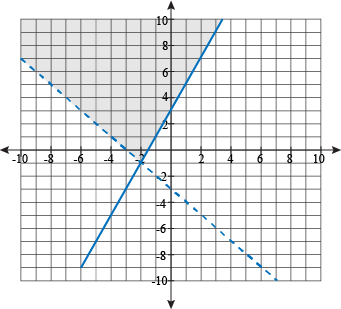
Answers vary
500
If a matrix has 3 0's on the top or bottom the answer will be....
Infinitely many