Solve the following system by graphing:
y = 3x - 3
y = -x +1
(1,0)
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
Is the given point a solution to the system of equations?
Point: (2,6)
3x + 2y =18
8x - 4y = 8
Two racers are competing. Racer A travels 4 meters every second and racer B travels 12 meters every second. Racer A recieved a head start of 40 meters. When will the two meet?
Racer A: y = 4x + 40
Racer B: y = 12x
Solution: (5, 60) so they meet 5 seconds into the race at the 60 meter mark.
1.How many solutions are there and why?
2. What can you say about the slopes of both lines?

1.No Solutions since the two lines are parallel and so they never cross
2. Slopes must be the same since they are parallel
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
Solve the systems of equations using Elimination:
-2x + y =3
6y + 2x = 4
Hint: Re-arrange your equations to line up your variables first!
(-1,1)
1. Which method(s) for solving systems of equations should be used to get the most accurate results?
2. Which method(s) only provide an estimated solution?
1. Elimination and substitution provide exact answers
2. Graphing is at best an estimate
The difference of two numbers is 12. Their sum is 54. Find the smaller of the two numbers
x + y = 54
x - y = 12
(33, 21)
the smaller number is 21
Solve Using Graphing:
y = 5/3x + 2
y = -3
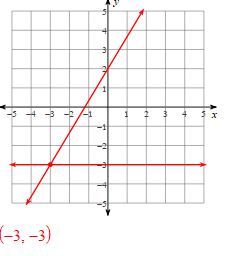
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
Solve the systems of equations using Elimination:
-6x - 10y = 4
-3x - 5y = 7
No Solution
Which method would be most efficient to solve the following systems AND WHY:
1. y = 3x +4
x+2y = 11
2. 3x-4y=11
6x-8y = 22
3. y = 1/2x +4
y = 3x -4
1. Substitution since 1 variable is isolated
2. Elimination since both equations are in standard form
3. Graphing since both equations are in slope-intrcept form and there is a fraction slope.
There are two numbers, the sum is 22. The larger number is one more than twice the smaller number. What are the two numbers?
x + y = 22
y = 2x +1
(7, 15)
Draw an example of each of the 3 types of solutions that systems can have.
Infinitely Many Solutions - lines overlap
No solutions - lines are parallel
One solution - lines cross at 1 point.
Solve the systems of equations using substitution:
-8x - 5y = -24
y - 10 = x
(-2, 8)
Draw an alligator at a barber shop
answers may vary
Diego was solving 3 systems of equations and this is the final line of his work for each:
1. 0 = 0
2. 0 = -4
3. y = 5 , x = -3
How many solutions do each of the systems have?
2. No solutions (false statement)
3. 1 solution
Diego decides to buy some walnuts and raisins, where walnuts cost 6$ a pound and raisins cost 9$ a pound. Diego spends a total of 21$ and buys a total of 3 pounds of nuts and raisins combined. How many pounds of walnuts and how many pounds of raisins did Diego buy?
Hint: set-up two equations in standard form (Ax+By=C)
6x + 9y = 21
x + y = 3
(2,1) - 2 pounds of walnuts and 1 pound of raisins
1.Solve the systems of linear equations by graphing
2. Why would we use graphing here as opposed to substitution, even though both equations have y isolated?
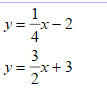
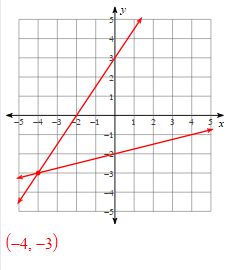 2. fraction slopes are easy to graph but annoying to work with algebraically
2. fraction slopes are easy to graph but annoying to work with algebraically
Solve the systems of equations using substitution:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
Solve the systems of equations using Elimination:
-5x + 2y = -12
4x - 3y = 11
(2, -1)
DRAW HARRY POTTER GETTING DUNKED ON
answers may vary
A cycle shop has a total of 36 bicycles and tricycles in stock.
Collectively there are 80 wheels.
How many bikes and how many tricycles are there? Solve in any way you wish
Let x = number of bicycles
Let y = number of tricycles
Hint: Both equations should be in standard form and the equation relating to the wheels should have the numbers 2 and 3 in there somewhere.
x + y = 36
2x + 3y = 80
(28, 8) - 28 bicycles and 8 tricycles