What is the solution?

(-1,1)
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
Is the given point a solution to the system of equations?
Point: (2,6)
x + y = 8
3x - y = 0
Yes
Which way would you shade the line?
x < -7
Left
How many solutions are there?

No Solutions
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
Solve the systems of equations using Elimination:
-3x - 5y = 2
3x + 5y = 7
No Solution
Is the given point a solution to the system of equations?
Point: (1/2, -2)
6x + 5y = -7
2x - 4y = -8
No
Write an inequality for the story:
Courtney and Zaria have 23 dollars to spend on school supplies. If they buy a pack of pencils for 1.50$, paper for 0.42$ and binders for 4.74$.
23>15.x+.42y+4.74z
Solve Using Graphing:
y = 5/3x + 2
y = -3
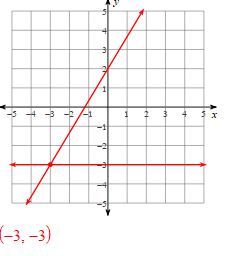
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
Solve the systems of equations using Elimination:
-6x - 10y = 4
-3x - 5y = 7
No Solution
What is true of lines with no solution?
They are parallel
-or-
They have the same slope, but different intercepts
Whaich way would you shade for this equation
y>2x+1
Above
How many solutions are there?
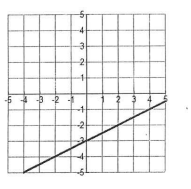
Infinitely Many Solutions
Solve the systems of equations using substitution:
-8x - 5y = -24
-x + y = 10
(-2, 8)
Solve the systems of equations using Elimination:
x + 8y = 22
3x + 4y = -14
(-10, 4)
What would you multiply the top equation by if you wanted to eliminate the "x" terms:
0.3x - 0.2y = -2.1
0.6x + 1.3y = 0.9
-2
Write a system of inequalities to represent the graph: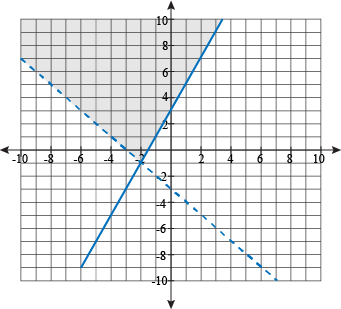
y > x - 3
y > 2x + 3
Solve the systems of linear equations by graphing:
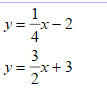
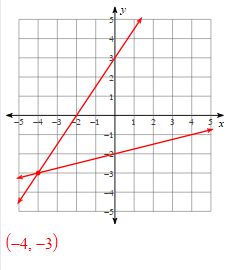
Solve the systems of equations using substitution:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
Solve the systems of equations using Elimination:
-5x + 2y = -12
4x - 3y = 11
(2, -1)
What does it mean if a system of equations has infinite solutions?
The lines are equal.
Solve the inequality for scenario:
Maddy and Tots have 35 dollars for spending money at the fair. They are getting lunch and spend 18.56$ on 6 tacos and 2 burritos. They then plan to use the rest of the money on games while at the fair. If all the games are 1.50$ to play how much games can they play?
10 games