Solve by Graphing
Solve by Substitution
Solve by Elimination
Linear Inequalities
Miscellaneous
100
What is the solution?
(-1,1)
100
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
100
< and > indicate that you should draw what kind of line?
Dashed
100
Is the given point a solution to the system of equations?
Point: (2,6)
x + y = 8
3x - y = 0
Yes
200
How many solutions are there?
No Solutions
200
Is (-5, -3) a solution to the system of equations?
5x - 5y = -10
y = -4x -17
No
200
Solve the systems of equations using Elimination:
-3x - 5y = 2
3x + 5y = 7
No Solution
200
Greater than and greater than or equal to symbol mean you shade _______ your inequality
above
200
Describe the graph of a system with 1 solution.
Intersecting Lines
300
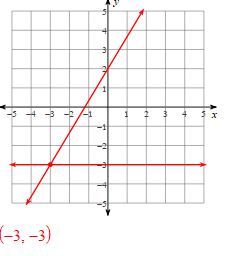
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
What would the equation look like if you solve the system of equations using substitution:
y = -2x - 9
3x -6y = 9
3x - 6(-2x - 9) = 9
300
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = 0
No Solution
300
What is the rule that we have to remember when multiplying or dividing by a negative coefficient with inequalities?
You have to flip the sign
300
What would you multiply the top equation by if you wanted to eliminate the "x" terms:
0.3x - 0.2y = -2.1
0.6x + 1.3y = 0.9
-2
400
How many solutions are there?
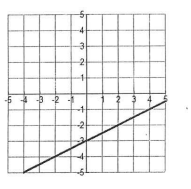
Infinitely Many Solutions
400
Which is easiest to solve the systems of equations using substitution:
1) Solve for y: -8x - 5y = -24
2) Solve for x: -x + y = 10
2) Solve for x
400
Solve the systems of equations using Elimination:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
400
Is the graph of the systems of equations correct?
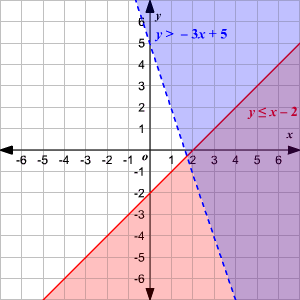
Yes
400
What is the name of a system with no solutions?
An Inconsistent System
500
Solve the systems of linear equations by graphing:
500
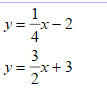
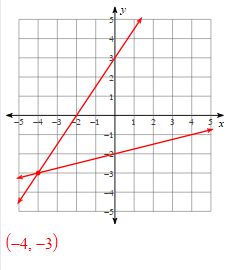
The equation below represents a systems of equations using substitution. What is the solution?
16x - 2(8x - 7) = 14
Infinitely Many Solutions
500
Solve the systems of equations using Elimination:
-15x + 6y = -36
8x - 6y = 22
(2, -1)
500
Give a solution to the system of inequalities graphed below: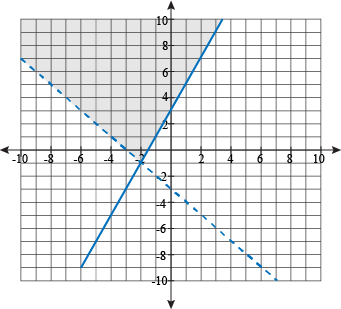
Answers vary
500
How many solutions does a system have when the graph show coinciding lines?
Infinitely many