Solve by Graphing
Solve by Substitution
Solve by Elimination
Strategy and Concepts
Misc (fastest)
100
What is the solution?
(-1,1)
100
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
100
What strategy would you use and explain why?
14x + 2y = 26
-14x - 6y = -50
elimination because the coefficients of x will cancel out.
100
Do the Check:Is the given point a solution to the system of equations? Show work
Point: (2,6)
x + y = 8
3x - y = 0
Yes
200
How many solutions are there?
No Solutions
200
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve the systems of equations using Elimination:
-3x - 5y = 2
3x + 5y = 7
No Solution
200
What strategy would you use and explain why?
-5x - 5y = 10
y = -4x -17
substitution because y is already solved for.
200
Do the Check: Is the given point a solution to the system of equations? Show work
Point: (1/2, -2)
6x + 5y = -7
2x - 4y = -8
No
300
Solve Using Graphing:
y=5/3x+2
y=-x-6
300
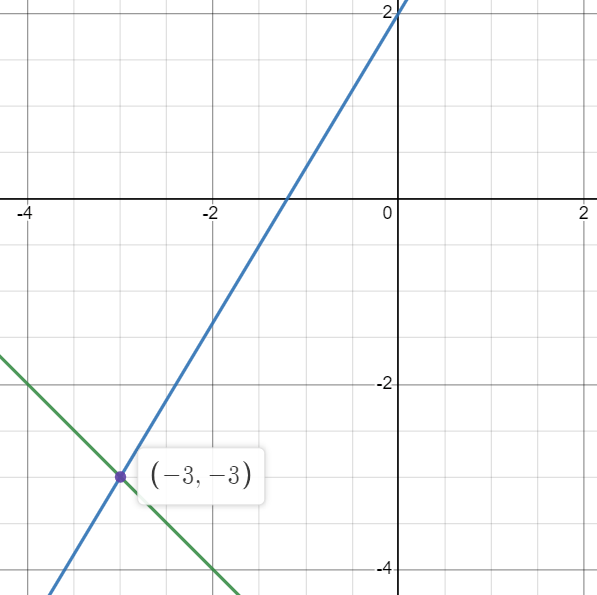
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = -4
Infinitely Many
300
Is there 1 solution, No solution, or Infinite solutions for the system of linear equations below? AND JUSTIFY WHY
3x - y = 19
-3x + y = 10
No Solutions because it is a false statement.
300
What is a coefficient?
The number in front of a variable
400
Find the solution by graphing
y=1/2x-3
-7y+7/2x=21
Infinitely Many Solutions
400
Solve the systems of equations using substitution:
-8x - 5y = -24
-x + y = 10
(-2, 8)
400
Solve the systems of equations using Elimination:
x + 8y = 2
3x + 4y = 26
(10,-1)
400
What graph does a system of equations with one solution look like? (use words, not images)
intersecting lines
400
Can a system of linear equations have exactly two solutions?
No
500
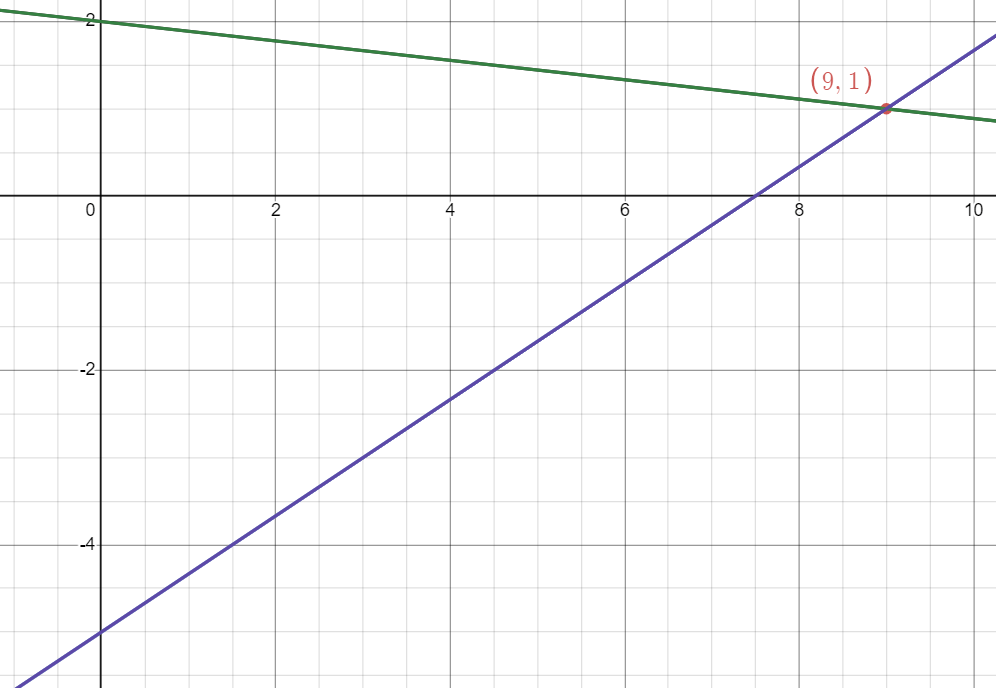
Solve the systems of linear equations by graphing:
9y+x=18
3y-2x=-15
500
Solve the systems of equations using substitution:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
500
Solve the systems of equations using Elimination:
-5x + 7y = -7
-2x - 2y = 2
(0, -1)
500
Name two forms of a linear equation?
**I'm not talking about methods...
slope-intercept
point-slope
standard form
500
What graph does a system of linear equations with no solutions look like? (use words, not images)
Parallel lines