Solve by Graphing
Vocabulary
Solve by Inspection
Number of Solutions
General
100
What is the solution?
(-1,1)
100
What is a system of equations?
Two or more equations in the same variable that can be solved at the same time.
100
How many solutions does the system have?
y=3x+5
y=4x+2
one
100
How many solutions would a system of linear equations have if the equations are parallel and different y-intercepts?
Zero Solutions
100
Write the equation of a line with a slope of 2 and a y-intercept of 3.
y = 2x + 3
200
How many solutions are there?
No Solutions
200
The solution to a system of equations that intersect is an ____________ _______.
ordered pair
200
How many solutions does the system have?
2x - 3y = 9
-2x + y = -2
one solution
200
How many solutions would a system of linear equations have if the equations are parallel and have the same y-intercept?
Infinite Solutions
200
Convert to slope-intercept form.
2x + 3y = 6
y = 2/3x + 2
300
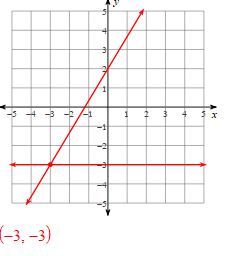
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
Lines that have no solution
parallel lines
300
How many solutions does the system have?
y = 4 + 6x
2y = 12x + 8
infinite solutions
300
Is there 1 solution, No solution, or Infinite solutions for the following question?
y = 19 - 3x
y = 10 - 3x
No Solutions
300
Determine if the ordered pair (2,1) is a solution to the system of equations.
2x + 4y = 8
x + 2y = 4
yes
400
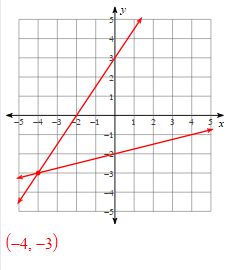
Solve this by graphing:
y = 2x - 4
y = -1/3 x + 3
(3,2)
400
Lines that have one solution
intersecting lines
400
If two lines intersect at a point, what does that indicate about the system of equations?
There is one solution
400
How many solutions does the system have?
y = 4/3x + 2
y + 4/3x + 2
These are the same exact line, therefore they have
Infinite Solutions
400
Describe the process for graphing this equation:
y = x + 2
Graph the y-intercept first.
Then from the y-intercept go up 1 and right 1 to find another point.
500
Solve the systems of linear equations by graphing:
500
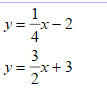
Lines that have infinitely many solutions
Coinciding Lines
500
How can you tell if a system has no solutions?
the equations will have the same slope and different/same y-intercepts
500
How many solutions does the system have?
y = -4x + 3
y = -x + 3
Different slopes
One solution
500
Write a system of equations that have infinite solutions.
will vary