Solve by Graphing
Solve by Substitution
Definitions
Word Problems
100
What is the solution to a system of equations that has been graphed?
The point of intersection or where the lines meet.
100
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
100
What is the equation y=mx+b called?
Slope Intercept Form
100
What is the first step to solve a word problem? (We do this before we even write the equations)
Define the variables - accept similar answers
200
How many solutions are there?
No Solutions
200
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
If a system of equations is made up of parallel lines, how many solutions does it have?
No Solutions
200
Does it matter which variables we choose to use in a word problem. For instance, can I use any letter to represent Hotdogs?
Explain your answer!
Teacher decides based on explanation.
Yes, we should choose variables that represent what we are trying to find and are easily recognizable.
But,
No because we can use any variable to represent any unknown value.
300
What is the solution?
(-1,1)
300
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Explain what solving through graphing means
Graphing two lines to find an intersection point, thus solving the system
300
Write an Equation for the sentence:
3 sodas and 4 bags of popcorn cost $19.
3s+4p=19
Accept other variables
400
How many solutions are there?
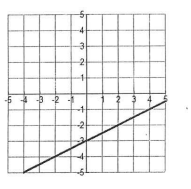
Infinitely Many Solutions
400
Solve the systems of equations using substitution:
-8x - 5y = -24
-x + y = 10
(-2, 8)
400
What does a system of inequalities look like when graphed.
Two lines that are solid or dashed and have a double shaded region as their solution.
Teacher decides if answer was good enough.
400
Write an equation for this sentence.
There were 4 times as many students as adults at the assembly.
S=4A
500
Solve the systems of linear equations by graphing:
500
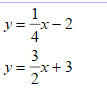
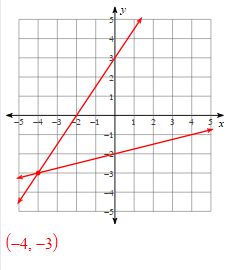
Solve the systems of equations using substitution:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
500
Explain the substitution method
Replacing a variable with its equivalent Expression to solve a system of equations - Or similar explainations
500
Solve the Word Problem:
Mrs. Brown has a few quarters and dimes. In total, she has $1.05 and the same amount of dimes as she has quarters.
0.10D+0.25Q=1.05
D=Q
3 Dimes and 3 Quarters