What is the solution?

(-1,1)
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
What strategy would you use?
14x + 2y = 26
-14x - 6y = -50
elimination
Graphically, solutions of a system of two equation correspond to this.
What is points of intersection?
How many solutions are there?

No Solutions
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
Solve the systems of equations using Elimination:
-3x - 5y = 2
3x + 5y = 7
No Solution
What strategy would you use?
-5x - 5y = 10
y = -4x -17
substitution
The first step in solving in a system of equations by substitution..
What is solve one of the equations for one variable in terms of the other?
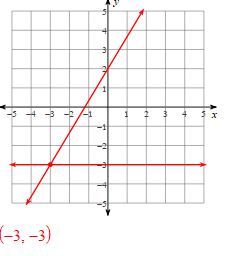
Solve Using Graphing:
y = 5/3x + 2
y = -3
Solve the systems of equations using substitution:
x + y = - 9
5x -8y = 20
(-4, -5)
Solve the systems of equations using Elimination:
3x + 4y = -26
2x + 5y = 18
(-2, -5)
Is there 1 solution, No solution, or Infinite solutions for the system of linear equations below?
3x - y = 19
-3x + y = 10
No Solutions
The 4 methods we learned in this class to solve systems of equations.
What is
1. Substitution
2. Elimination
3. Graphing
4. Gaussian elimination or row echelon form
How many solutions are there?
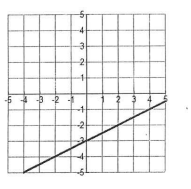
Infinitely Many Solutions
Solve the systems of equations using substitution:
2x - y2 = 0
x - y = 4
(8, 4), (2,-2)
Solve the systems of equations using Elimination:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
P = 500 - 0.4x
P = 380 + 0.1 xWhat is (240, 404)?
When enough units have been sold so that the total revenue R equals the total cost C.
What is the break-even point?
Solve the system graphically.
2x + y < 4
2x - y > 0
X > 0
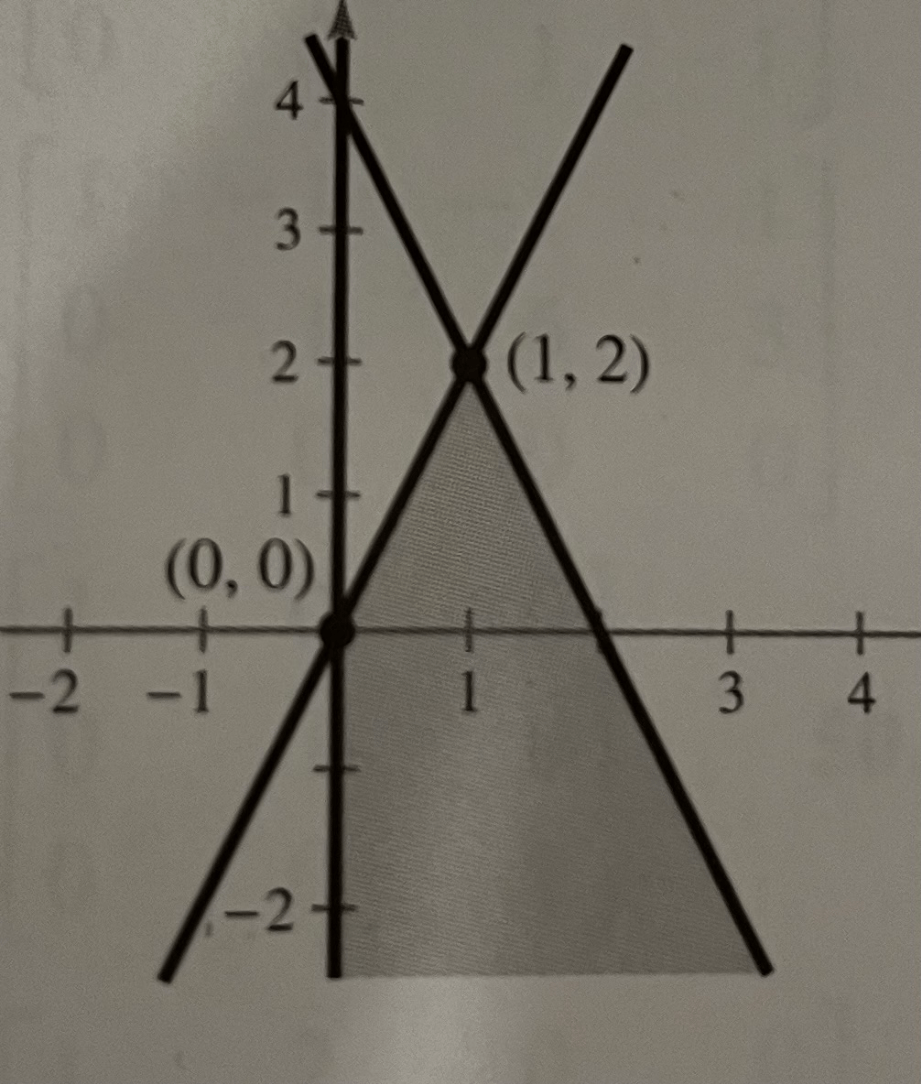
Two numbers have a sum of 117. The larger number is 42 less than twice the smaller number.
What are the numbers.
What is the larger number is 64 and the smaller number is 53?
Solve
4x -2y + z=13
3x -y +2z= 13
x+ 3y -3z=-10
(2, -1, 3)
A total of $12,000 is invested in two funds paying 5% and 3% simple interest. The annual interest is $500.
How much is invested at each rate?
What is $7000 is invested at 5% and $5000 is invested at 3%?
Georgia bought 3 pens and 4 notebooks for $26.50 from the bookstore. She later bought 7 pens and 5 notebooks for $41.25 from the same bookstore. How much would you have to pay for 2 pens and 2 notebooks?
Pens $2.50 each
Notebooks $4.75 each
$14.50