What is the solution?

(-1,1)
Solve the systems of equations :
y=3x-10
x=2
(2,-4)
Solve the systems of equations using Elimination:
-x - 5y = 4
x + 7y = -8
(6, -2)
How many solutions would a system of linear equations have if the equations are parallel and different y-intercepts?
Zero Solutions
Write the system given the following situation.
Stefan sold 3 senior citizen tickets and 1 child ticket for a total of $38. Marie sold 3 senior citizen tickets and 2 child tickets for a total of $52.
3x+y=38
3x+2y=52
How many solutions are there?

No Solutions
Solve the systems of equations:
y=2x-10
y=4x+8
(-9,-28)
Solve the systems of equations using Elimination:
2x - 3y = 9
-2x + y = -2
(-1, -4)
How many solutions would a system of linear equations have if the equations are parallel and have the same y-intercept?
Infinite Solutions
The sum of two numbers is 12 and their difference is 4.
x+y=12
x-y=4
Solve Using Graphing:
y = 5/3x + 2
y = -3
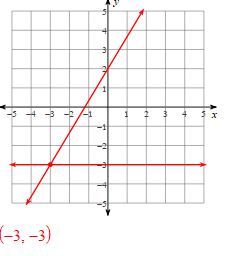
Solve the systems of equations:
y = -2x - 9
3x -6y = 9
(-3, -3)
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = 0
No Solution
Is there 1 solution, No solution, or Infinite solutions for the following question? (Menu 75, Menu 711)
3x - y = 19
-3x + y = 10
No Solutions
Write the equations for the following system.
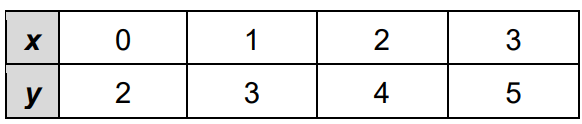
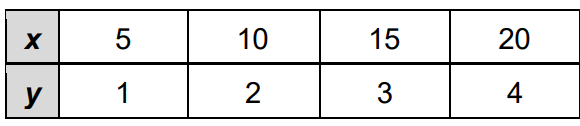
y=x+2
y=1/5x
Solve this by graphing:
y = 2x - 4
y = -1/3 x + 3
(3,2)
Solve the systems of equations:
2x - y = 6
x = y + 5
(1, -4)
Solve the systems of equations using Elimination:
-3x - 24y = -66
3x + 4y = -14
(-10, 4)
How many solutions does the system have? (Menu 75, Menu 711)
3y + 4x = 6
12y + 16x = 24
These are the same exact line, therefore they have
Infinite Solutions
Write the system of equations for the following situation.
Jessica has quarters and nickels in her purse. She has 22 coins that total to $4.10.
x+y=22
0.25x+0.10y=4.10
Solve the systems of linear equations by graphing:
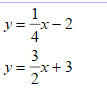
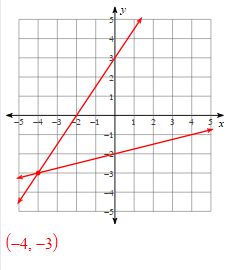
Solve the systems of equations:
y = 8x -7
16x - 2y = 14
Infinitely Many Solutions
Solve the systems of equations using Elimination:
-15x + 6y = -36
-4x + 3y = -11
(2, -1)
How many solutions does the system have?
-6y + 2 = -4x
y - 2 = x
Different slopes
One solution
y=2/3x+1/3
y=x+2
Write a system of equations that represent the following situation.
Seth and Amber baked cookies last week. Seth baked 4 less than twice the number of cookies Amber baked. Together they baked 52 cookies.
x=2y-4
x+y=52