Facts about Systems
How Many Solutions?
What is the Next Step?
Substitution
Miscellaneous
100
How many equations are in a system of linear equations?
2 equations
100
What are the three possible solutions we have learned for a System of Linear Equations?
One solution, No solutions, Infinitely Many Solutions
100
What is the next step?
2x=4
Divide by 2 on each side
100
Solve this System of Linear Equations using Substitution.
y=5
y=3x+8
x=-1
y=5
Final Answer: (-1, 5)
100
Multiply:
(x+1)(x-5)
x2 - 4x - 5
200
What is the goal when solving a System of Linear Equations?
To find the value of both variables in the system
200
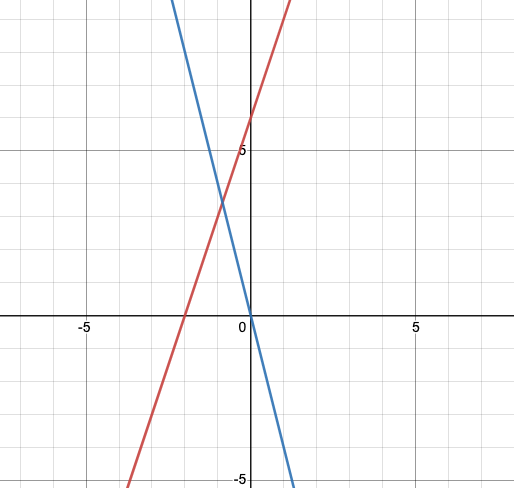How many solutions are there in this System of Linear Equations?
1 solution
200
What is the next step?
3x-9=3
Add 9 to both sides
200
Solve for x.
5(x-2) = 2x+10
Final Answer: x = 20/3
200
Another name for the "slope" of a line.
Rate of Change
300
How can we tell that our equations are linear?
They have an exponent of 1 or the graph formed by the system only contains lines.
300
How many solutions are in this System of Linear Equations?
y=3x-8
y=3x+4
No Solutions
300
What is the next step?
3x+6+4x=-1
Combine the variable terms because they are like terms. (3x+4x)
300
Solve this System of Linear Equations using Substitution.
y = 4 - x
y = 3/2 - (1/2)x
x = 5
y = -1
Final Answer: (5, -1)
300
Is (3,13) a solution to this system of equations? (Show your work for this question)
y = 5x - 2
y = 4x + 2
No
400
What are the two methods we learned to solve a system of linear equations?
Solving a system of equations graphically or algebraically
400
How many solutions are in this System of Linear Equations?
y=
-19x+8
y=19x+8
1 Solution
400
What is the next step?
y=3x+4
y=8-2x
Set the equations equal to each other.
400
Solve for x:
(5/8)x + 4 = 14
x = 16
400
If a system of equations has no solution, then the graph formed by the system has _________ lines.
Parallel
500
When you solve a System of Linear Equations, what should our answer look like?
(x, y)
500
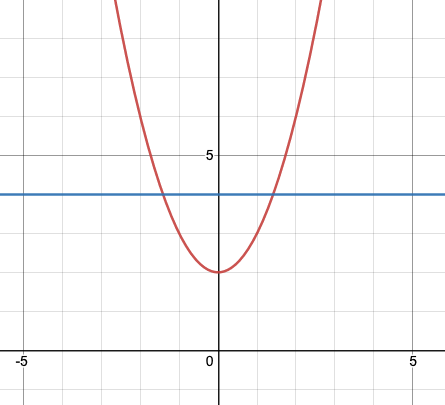How many solutions are in this system of linear equations?
2 solutions
500
What is the next step?
3x-8y=37
3x+6y=9
Graph it!
500
Solve for x:
(1/3)(x - 3) = (5/4)x + 2
x = -36 / 11
500
A system of equation is graphed and the lines formed by the graph overlap. How many solutions does this system have?
Infinitely many solutions