Solve by Graphing
Solve by Substitution
Solve by Elimination
Mixed
Other Topics
100
What is the solution?
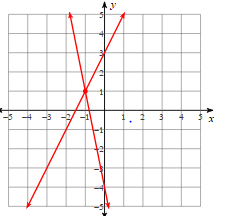
(-1,1)
100
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
100
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
100
What strategy would you use?
14x + 2y = 26
-14x - 6y = -50
Elimination
100
Is the given point a solution to the system of equations?
Point: (2,6)
x + y = 8
3x - y = 0
Yes
200
How many solutions are there?
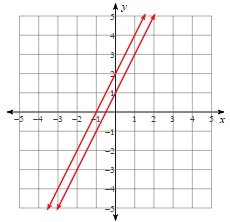
No Solutions
200
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
200
Solve the systems of equations using Elimination:
-3x - 5y = 2
3x + 5y = 7
No Solution
If we add these equations together, both x and y are eliminated. Leaving us with 0 = 9, which is impossible
200
What strategy would you use? Bonus 200 points, if you can solve it!
-5x - 5y = 10
y = -4x -17
Substitution
Point of Intersection is (-5,3)
200
Is the given point a solution to the system of equations?
Point: (-2, -2)
6x + 5y = -7
2x - 4y = -8
No
However, (-2,1) is a solution
300
Solve Using Graphing:
y = 5/3x + 2
y = -3
300
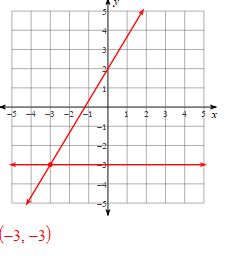
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
300
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = 0
No Solution
300
Is there 1 solution, No solution, or Infinite solutions for the system of linear equations below?
3x - y = 19
-3x + y = 10
No Solutions
300
What are the three types of Solutions we have learned about with Systems of Equations?
Draw an example of each, with correct labels
Infinite Solutions: Should be two lines that are the exact same
Zero Solutions: Two parallel lines that do not intersect
One Solution: Two lines that intersect at one point
400
How many solutions are there?
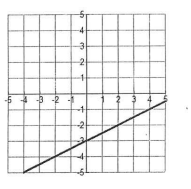
Infinitely Many Solutions
400
Solve the systems of equations using substitution:
-8x - 5y = -24
y = -x +10
(-2, 8)
400
Solve the systems of equations using Elimination:
3x + 24y = 66
3x + 4y = -14
(-10, 4)
400
How many solution would the following System of Equations have? No work required
2x - 4y = 12
2x + 14y = 23
No Solutions
They have the same slope, (the coefficient in front of x) they are parallel
400
Solve using Elimination
-3x +2y = 21
6x + 13y = 9
We first need to multiple the top equation by 2, making the coefficients of x opposite. Once we add them together we can solve for y, then x
(-5,3)
500
Solve the systems of linear equations by graphing:
500
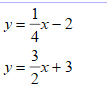
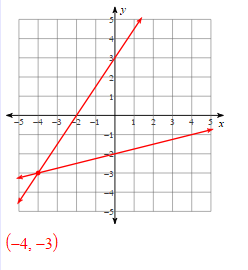
Solve the systems of equations using substitution:
8x + y = 7
16x +2y = 14
Infinitely Many Solutions
There are the same line, all that's different is that the second equation was multiplied by 2
500
Solve the systems of equations using Elimination:
-15x + 6y = -36
8x - 6y = 22
(2, -1)
500
How many solutions would the following Systems of Equations have?
5x - 13y = 1
10x -26y = 2
Infinite Solutions
They are the same line, because the second equation is just the first line multiplied by 2
500
Alex Had 15 more magnets than Kevin at first. After Alex gave away 29 magnets and Kevin bought another 10 magnets, Kevin had 3 times as many magnets as Alex. How many magnets did Alex and Kevin have altogether at first?
what is 67?