Section
2-1 and 2-2
2-1 and 2-2
Section
2-3 and 2-4
2-3 and 2-4
Section
2-7 and 2-8
2-7 and 2-8
Section
2-10
2-10
Chapter 1
Review
Review
100
What is the key takeaway from sections 1 and 2?
Equivalent equations are equations that have the same solution. The solution can be obtained using the properties of equality and inverse operations.
100
What is a Key takeaway from section 3 or 4?
1) We can use the properties of real number to simplify and solve Multi-step equations
2)To solve equations with variables on both sides, you can use the properties of equality and inverse operations to write a series of simpler equivalent equations.
100
What is the key takeaway from sections 7 and 8?
If two ratios are equal and a quantity in one of the ratios is unknown, you can write and solive a proportion to find the unknown quantity.
100
What is the key takeaway from section 10?
You can find a percent change when you know the original amount and how much it changed.
100
What is a key takeaway from Chapter 1, section 9?
Sometimes the value of one quantity can be found if you know the value of another. You can represent the relationship between the quantities in different ways, including tables, equations and graphs.
200
This is an example of what property?
x+7-7= 21-7
Subtraction property of equality
200
Solve for u
3u+6=18
u=4
200
2/3=x/27
x=18
200
Mrs. Cogley teaches classes during the day. She offers a discount for siblings taking the same class. If she charges $55 per student, but $90 for two students, how much of a discount is she offering per student?
18% off per student
200
True or False:
x/2+1/2=(x+1)/4
False
300
Solve for j
4/3J=8/9
j=2/3
300
-2(x/4+3/4)=x-1
x=-1/3
300
((l+2))/5=(2(l-1))/2
l=7/4
300
Mr and Mrs. Cogley grew carrots this summer. They determined that they spent $0.75 per carrot as they grew. If they wanted to sell them at the farmers market for a 40% mark-up, about how much should they sell them for?
$1.05
300
Write the algebraic expression for the following statement:
The four more than than quotient of a number “w” and 3
w/3+4
400
The air temperature beneath the Earth’s surface increases by about 10 degrees celsius every kilometer. If we were to dig a hole straight down, and it is -34 degrees outside, how far would we have to go down before we got above freezing (zero degrees)
3.4 Kilometers
400
Mr. Cogley takes Mrs. Cogley out for dinner on a date night. He buys her some flowers and chocolates. Each flower costs $2 and each box of chocolate costs $7.50. If he spends $21.50 and only buys one box of chocolate, how many flowers did he buy for her?
7 flowers
400
In a 3 hour session, Mr. Cogley was able to split 24 logs for his fireplace. If Mr. Cogley needs to split 52 more rounds, how many hours of splitting wood does he need to set aside to get ready for winter?
6 hours and 30 Minutes
400
Mr. Cogley is really trying to finish his thesis. He goes into the lab and makes the compound he is studying for his thesis. When he is finished he weighs his final product and it is 0.60 grams. He does the math and calculates that he should have made 0.75 grams. What is his percent recovery? (Hint: Percent recover = 100%-p%)
80% recovery
400
Write an equation given the following table and graph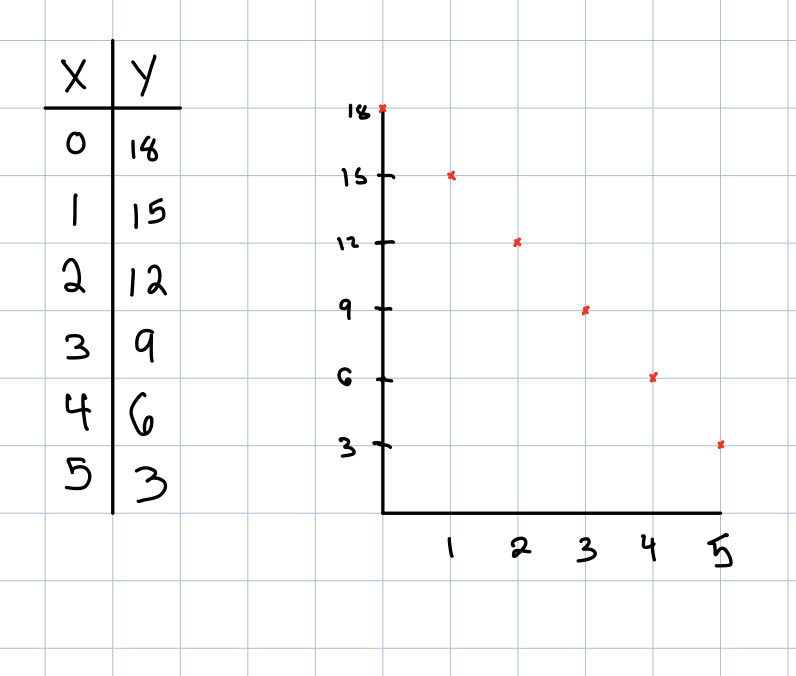
y=-3x+18