Distribute the Goods
The Standards of Normalness
Standards of InNormalness
Costco Samples
100
The type of Distribution shown here: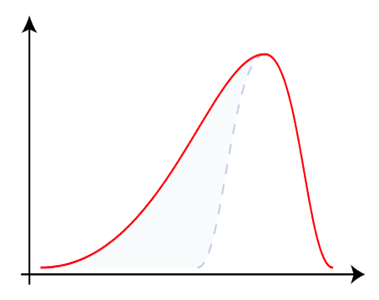
Left Skewed: Looks like your left hand
100
Give a definition of the z-score.
The number of standard deviations away from the mean
100
The national average SAT score (for Verbal and Math) is 1028. If we assume a normal distribution with standard deviation of 92, what is the probability that a randomly selected score exceeds 1200 (include calculator function and sketch)?
normalcdf(1200, E99, 1028, 92) = 0.0308
100
Give the "formulas" for the mean and standard deviation of Sampling Distributions, using the correct formulas
200
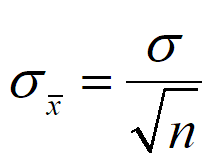
What are the values of the mean and standard deviation for standard normal distributions?
\mu=0, \sigma=1
200
Give the z-score corresponding to a probability of less than 73% in a standard normal distribution (with calculator entry and graph sketch).
What is invNorm(0.73,0,1)=0.6128
200
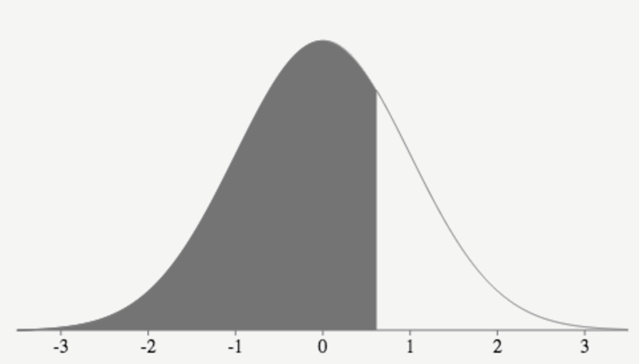
Give the z-score for the given area below: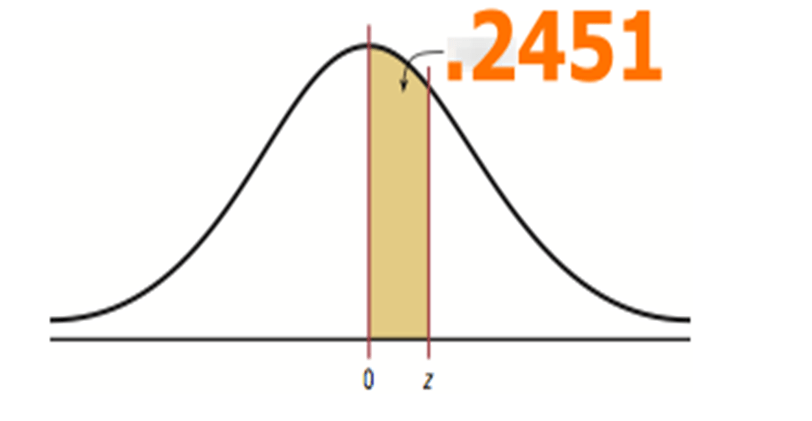
invNorm(0.7451,0,1) = 0.6591
200
A survey found that the American family generates an average of 17.2 pounds of glass garbage each year. Assume the standard deviation of the distribution is 2.5 pounds. Determine the values of glass garbage for the middle 40% of all glass garbage per family (include calculator function and sketch). Answer in CONTEXT of the PROBLEM.
invNorm(0.4,17.2,2.5, CENTER) = 15.89, 18.51
OR
invNorm(0.3, 17.2, 2.5) = 15.89
invNorm(0.7, 17.2, 2.5) = 18.51
The middle 40% of families generate between 15.89 and 18.51 lbs of glass garbage yearly.
300
What distribution has a median that is greater than the mean?
Left Skewed
300
Give the probability that your randomly chosen girlfriend/boyfriend has an IQ that is more than 2.47 standard deviations above the mean (with calculator entry and sketch).
normalCDF(2.47, E99, 0, 1)= 0.0068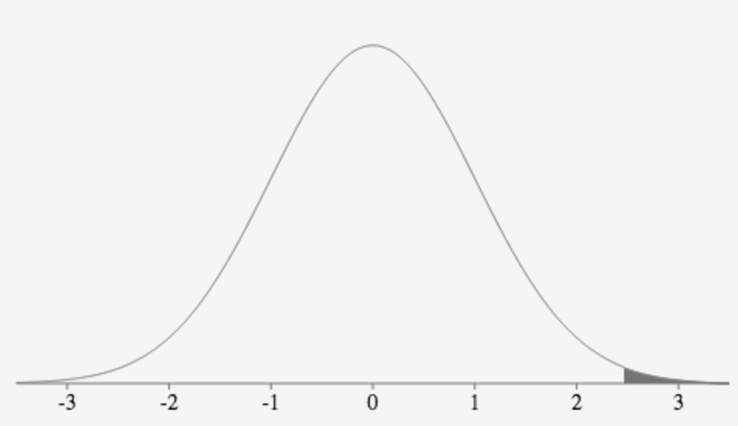
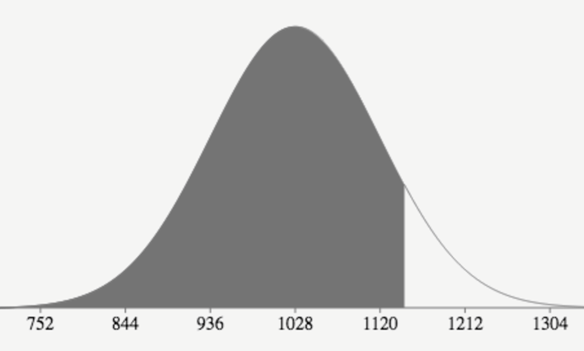
300
The national average SAT score (for Verbal and Math) is 1028. If we assume a normal distribution with standard deviation of 92, what is the 90th percentile score? (include calculator function and sketch)?
invNorm(0.9, 1028, 92) = 1145.9
300
A survey found that men spend on average $200 a month dining out with a standard deviation of $30. Assume the variable is approximately normal. Find the probability that 40 men selected at random spend an average of at most $205 a month (include calculator function and sketch). Answer in CONTEXT of the PROBLEM?
normalcdf(-E99, 205, 200, 30/sqrt40) = 4.7434
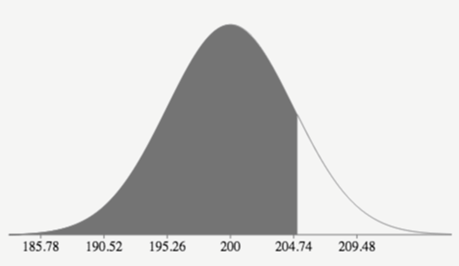
There is an 85% probability that in a random sample of 40 men, their average amount spent on dining out is at most $205.
400
Draw a pig in a blanket
400
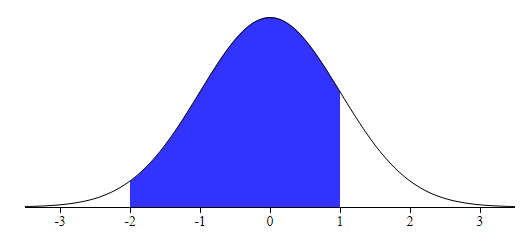
The probability that your randomly chosen z-score is between -2.00 and 1.00.
normalCDF(-2, 1, 0, 1) = 0.819
400
What can you keep after giving it to someone?
A promise, your word
400
A recent study of the lifetimes of cell phones found the average is 24.3 months. The standard deviation is 2.6 months. If a company provides its 33 employees with a cell phone, find the probability that the mean lifetime of these phones will be less than 23.8 months (include calculator function and sketch)? Answer in CONTEXT of the PROBLEM.
normalcdf(-E99, 23.8, 24.3, 2.6/sqrt33) = 0.1346
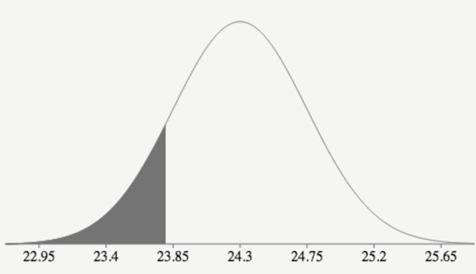There is a 13.5% probability that in a random sample of 33 users, their average lifetime of their cellphone is less than 23.8 months.