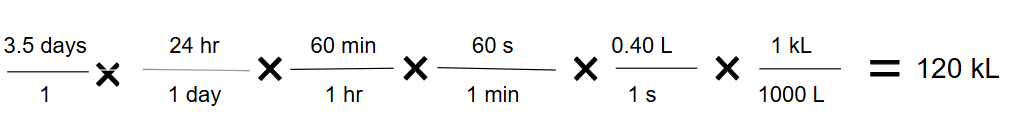States of Matter
Metric Units
Measurement
Derived Units & Dimensional Analysis
100
The image shows a particle model of a substance . Identify the state of matter shown and describe the motion of the particles.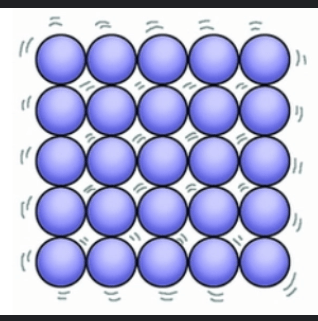
The state of matter is Solid. The particles are held in fixed positions and are only capable of vibrational motion (vibrating in place).
100
What unit of measurement do scientist use to measure temperature?
Degrees Celsius
100
What is the primary purpose of using significant figures in a scientific measurement?
Significant figures are used to communicate the certainty or precision of the measuring instrument used to take the measurement.
100
The key concept for this topic is that a derived unit is created by doing math to two or more simple units. Name two examples of derived units
g/mL
m2
km/s
cm3
200
Why does a gas, but not a liquid, fill and take the exact shape of any container it is placed in? Refer to the intermolecular forces (IMFs) and particle spacing in your answer.
Gas particles have negligible (or very weak) intermolecular forces and move independently, causing them to spread out and fill the entire volume. Liquid particles have stronger IMFs which keep them closely packed and prevent them from expanding to fill the container.
200
The International System of Units (metric) uses a specific base unit to measure mass. Name this unit and the common piece of lab equipment used to measure it.
The SI base unit for mass is the gram (g). The equipment is a balance (or scale).
200
A student uses a ruler marked only in whole centimeters. They measure an object's length and estimate the final digit. If they record the length as 15.6 cm, identify the two certain digits and the one estimated (uncertain) digit.
The certain digits are 1 and 5 (the whole cm marks). The estimated (uncertain) digit is 6 (the decimal place the student guessed).
200
The derived unit for density is g/mL. If you have 10.0 grams of a substance and 2.0 milliliters of volume, what is the density, and what does the derived unit g/mL physically represent?
The density is 5.0 g/mL. The derived unit g/mL represents the mass contained in every single unit of volume (or: mass per unit volume).
300
According to the Kinetic Molecular Theory (KMT), what two factors determine whether a substance will be a solid, a liquid, or a gas? Explain how a chemist can change the state of matter from a gas to a liquid (condensation).
The two factors are Intermolecular Forces (IMFs) and Average Kinetic Energy (Temperature). To change a gas to a liquid, the chemist must decrease the temperature, which lowers the average kinetic energy and allows the IMFs to pull the particles closer together.
300
Explain the difference between the metric unit for length and the metric unit for volume. How is volume typically derived from a length measurement in the lab?
Length is measured in meters (m), which is a base unit. Volume is measured in liters (L) or cubic meters (m3), which is a derived unit. Volume can be derived by multiplying length×width×height (or m3).
300
State the rule for counting significant figures for the number 0.0250 grams. How many significant figures does this measurement have?
The rule is: Leading zeros (those before the first non-zero digit) are never significant. Trailing zeros (those at the end) are significant if a decimal point is present. This measurement has three significant figures (2, 5, and the final 0).
300
In chemistry, concentration is often measured in the derived unit grams per liter (g/L), where mass of solute is divided by volume of solution. If a lab tech prepares 5.0 Liters of a solution containing 75.0 grams of salt, what is the concentration? Explain which two simple units combine to make the final derived unit.
75.0 g / 5.0 L = 15.0 g/L.
The final concentration is 15.0 g/L. The two simple units that combine to form the derived unit g/L are grams (for mass) and Liters (for volume).
400
Most substances are denser as a solid than as a liquid. Explain this observation using a particle-level description of the two states, focusing on particle spacing and the definition of density (Mass/Volume).
In the solid state, particles are typically more closely packed (less empty space) than they are in the liquid state. Since density is mass per volume, fitting the same mass into a smaller volume results in a higher density.
400
Explain why metric prefixes like kilo and milli are essential for scientists. Use the kilo prefix to state the numerical relationship between a kilogram and a gram.
Metric prefixes allow scientists to easily express extremely large or small measurements without writing many zeros. The prefix kilo means 1000, so 1 kilogram=1000 grams.
400
A student pours 50.0 mL of water into a beaker that already contains 25 mL of a solution. Calculate the final total volume and report the answer with the correct number of significant figures, following the addition/subtraction rule.
50.0 mL+25 mL=75.0 mL.
Addition Rule: The final answer must be rounded to the least certain decimal place.
Final Answer: 75 mL
400
A solution has a concentration of 0.05 moles/L. If you measure out 4.0 Liters of the solution, how many moles of solute did you measure? Show the dimensional analysis setup that cancels the Liters unit.
500
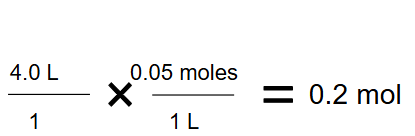
Imagine two samples of water: Sample A is water vapor at 110∘C and Sample B is liquid water at 90∘C. Which sample has particles with a higher average speed and which sample has particles with stronger effective intermolecular forces (IMFs)? Explain your reasoning for both.
Higher Average Speed: Sample A (water vapor at 110∘C) because temperature is a direct measure of average kinetic energy, and 110∘C is hotter than 90∘C.
Stronger Effective IMFs: Sample B (liquid water at 90∘C). Although the IMFs are present in both, they are effective only in the liquid, holding the particles close together. The particles in the gas (A) have sufficient kinetic energy to completely overcome these forces, making the forces largely ineffective in maintaining a fixed volume.
500
A sample of liquid is measured in a graduated cylinder to have a volume of 75 milliliters. Using the metric system's relationship between volume and length, express this volume in cubic centimeters (cm3) and explain why these two units are numerically identical.
75 milliliters is equal to 75 cubic centimeters (75 cm3). The reason they are identical is that the metric system defined the relationship such that 1 milliliter is exactly equal to 1 cubic centimeter (1 mL=1 cm3).
500
You have two balances: Balance A reads 15.4 g and Balance B reads 15.420 g. Explain which balance is more precise and how the number of significant figures indicates a lower potential for measurement error in that device.
Balance B (15.420 g) is more precise. The higher number of significant figures means the device can measure to more decimal places, resulting in a measurement that is closer to the true value and therefore has a lower inherent measurement error than a device that only measures to the tenths place.
500
A pump is used to transfer a liquid chemical at a constant rate of 0.40 Liters per second (0.40 L/s). If the pump runs continuously for 3.5 days, what total volume of liquid, in kiloliters (kL), was transferred? Show the full dimensional analysis setup.
